上海市杨浦区2020-2021学年八年级下学期期中数学试题

试卷更新日期：2022-03-10 类型：期中考试

进入出卷网下载

一、填空题

1. 一次函数y＝﹣2x﹣3的截距是．

查看试题解析
2. 已知一次函数y=(1－m)x＋m－2，当m时，y随x的增大而增大．

查看试题解析
3. 将一次函数y＝2x﹣3的图象向上平移个单位后，图象过原点．

查看试题解析
4. 当m取时，关于 x的方程mx+m＝2x无解．

查看试题解析
5. 已知一次函数y＝x+3k﹣2的图象不经过第二象限，则k的取值范围是．

查看试题解析
6. 已知一次函数 $y = k x + b (k \neq 0)$ 的图象如图所示，那么关于x的不等式 $k x + b > 0$ 的解集是．

查看试题解析
7. 方程 $\frac{x^{2} - 1}{x - 1} = 0$ 的解是.

查看试题解析
8. 二项方程 $\frac{1}{2}$ x⁴﹣8＝0的实数根是．

查看试题解析
9. 如果关于x的方程2﹣ $\sqrt{x - 2}$ +k＝0无实数解，那么k的取值范围是．

查看试题解析
10. 无理方程（x+4）• $\sqrt{x + 3}$ ＝0的解是．

查看试题解析
11. 用换元法解方程 $\frac{x - 1}{x^{2}} + \frac{2 x^{2}}{x - 1} = 3$ 时，如果设 $y = \frac{x - 1}{x^{2}}$ ，那么原方程化成关于 $y$ 的整式方程是

查看试题解析
12. 某服装厂准备加工400套运动装，在加工完160套后，采用了新技术，使得工作效率比原计划提高了20%，结果共用了18天完成任务，问计划每天加工服装多少套？在这个问题中，设计划每天加工x套，则根据题意可得方程为。

查看试题解析
13. 如果一个正多边形的每个外角都是30°，那么这个多边形的内角和为．

查看试题解析
14. 在平行四边形ABCD中，AE平分∠BAD交直线BC于点E，BE：EC＝2：1，且AB＝6，那么这个四边形的周长是．

查看试题解析
15. 在▱ABCD中，AB＝5，BC＝7，对角线AC和BD相交于点O，如果将点A绕着点O顺时针旋转90°后，点A恰好落在平行四边形ABCD的边AD上，那么AC的长是．

查看试题解析

二、单选题

16. 以下函数中，属于一次函数的是（　　）

A、 $y = \frac{x}{2}$ B、y＝kx+b（k、b为常数） C、y＝c（c为常数） D、 $y = \frac{2}{x}$

查看试题解析
17. 下列方程中，在实数范围内有解的是（　　）

A、x²﹣x+1＝0 B、 $\sqrt{2 x - 1}$ +2＝0 C、 $\frac{1}{x - 5} = \frac{x - 4}{x - 5}$ D、 $\sqrt{x - 2} + \sqrt{2 - x} = 0$

查看试题解析
18. 已知一次函数y＝kx﹣k，若函数值y随着自变量x值的增大而增大，则该函数的图象经过（　　）

A、第一、二、三象限 B、第一、二、四象限 C、第二、三、四象限 D、第一、三、四象限

查看试题解析
19. 如图，已知直线MN：y＝kx+2交x轴负半轴于点A，交y轴于点B，∠BAO＝30°，点C是x轴上的一点，且OC＝2，则∠MBC的度数为（　　）

A、75° B、165° C、75°或45° D、75°或165°

查看试题解析

三、解答题

20. 解方程： $\frac{3 x - x^{2}}{x^{2} - 1} = 2 - \frac{1}{1 - x}$

查看试题解析
21. 解方程： $\sqrt{3 x + 6} - \sqrt{x + 3} = 1$ ．

查看试题解析
22. 解方程组： ${\begin{array}{l} x^{2} - 6 x y + 9 y^{2} = 4 (1) \\ x - 2 y = 3 (2) \end{array}$

查看试题解析
23. 某地区为了进一步缓解交通拥堵问题，决定修建一条长8千米的公路．如果平均每天的修建费y（万元）与修建天数x（天）之间在50≤x≤100时具有一次函数关系，如表所示：

x（天）

60

80

100

y（万元）

45

40

35

(1)、直接写出y关于x的函数解析式是；

(2)、后来在修建的过程中计划发生改变，政府决定多修3千米，因此在没有增减建设力量的情况下，修完这条路比计划晚了21天，求原计划每天的修建费？

查看试题解析
24. 如图，平行四边形ABCD中，AD=2AB，E为AD的中点，CE的延长线交BA的延长线于点F．

(1)、求证：FB=AD．

(2)、若∠DAF=70°，求∠EBC的度数．

查看试题解析
25. 现有一段20千米长，可供长跑爱好者跑步的笔直跑道MN，已知甲、乙两人都从M点出发，甲跑到途中的P点后原地休息了20分钟，之后继续跑到N点，共用时间2小时；乙虽然比甲晚出发半小时，但和甲同时到达N点．假设两人跑步均为匀速，在甲出发后的2小时内两人离开M点的距离y（千米）与时间x（小时）的函数关系如图所示．请回答下列问题：

(1)、图中B点的坐标为

(2)、甲从点P跑到点N的速度为千米/时；

(3)、求图中线段CD的表达式．并写出定义域．

查看试题解析
26. 如图，在平面直角坐标系中，直线y=2x与反比例函数y= $\frac{k}{x}$ 在第一象限内的图像交于点A（m，2），将直线y=2x向下平移后与反比例函数y= $\frac{k}{x}$ 在第一象限内的图像交于点P，且△POA的面积为2.

(1)、求k的值；

(2)、求平移后的直线的函数解析式.

查看试题解析
27. 如图，已知一次函数y＝﹣x+7与正比例函数y＝ $\frac{4}{3}$ x的图象交于点A，且与x轴交于点B．

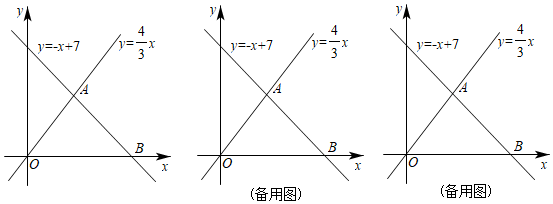(1)、求点A和点B的坐标；

(2)、过点A作AC⊥y轴于点C，过点B作直线l∥y轴，动点P从点O出发，以每秒1个单位长的速度，沿O﹣C﹣A的路线向点A运动；同时直线l从点B出发，以相同速度向左平移，在平移过程中，直线l交x轴于点R，交线段BA或线段AO于点Q．当点P到达点A时，点P和直线l都停止运动．在运动过程中，设动点P运动的时间为t秒（t＞0）．
①当t为何值时，以A、P、R为顶点的三角形的面积为8？

②是否存在以A、P、Q为顶点的三角形是AP＝AQ的等腰三角形？若存在，求t的值；若不存在，请说明理由．

查看试题解析

x（天）	60	80	100
y（万元）	45	40	35