上海市普陀区2020-2021学年八年级下学期期中数学试题
试卷更新日期：2022-03-10 类型：期中考试
一、单选题
-
1. 下列四个函数中，一次函数是（ ）A、y＝x2﹣2x B、y＝x﹣2 C、 D、y＝+12. 一次函数y＝（k+3）x+1中，y随x的增大而减小，则k的取值范围是（ ）A、k＞0 B、k＜0 C、k＜﹣3 D、k＞﹣33. 在梯形ABCD中，AD∥BC，AB﹦CD，那么下列结论中正确的是（ ）．A、 与 是相等向量； B、 与 是相等向量； C、 与 是相反向量； D、 与 是平行向量．4. 下列四个命题中，真命题是（ ）A、对角线互相垂直的四边形是菱形 B、对角线互相平分且垂直的四边形是矩形 C、顺次连接矩形四边中点得到的四边形是菱形 D、对角线互相垂直相等的四边形是正方形
二、填空题
-
5. 若函数y=（m-2）x+5是一次函数，则m满足的条件是 ．6. 将直线 沿y轴向下平移4个单位，那么平移后直线的表达式是7. 已知函数f（x）＝x﹣1，则f（2）＝ ．8. 一次函数y＝3（x﹣2）在y轴上的截距是 ．9. 若点A(x1 ， y1)，B(x2 ， y2)都在一次函数y＝﹣x+3的图象上，x1＜x2 ， 则y1﹣y20（填“＞”“＜”或“＝”）．10. 如果一个多边形的内角和为1440°，则这个多边形的边数为 ．11. 菱形的两条对角线的长分别为6和8，则这个菱形的周长为.12. 已知四边形ABCD中，A=B=C=90 ， 如果添加一个条件，即可推出该四边形是正方形，那么这个条件可以是 ．13. 如图，一次函数y＝kx+b的图象经过点(4，0)与(0，4)，那么关于x的不等式kx+b＞0的解集是 ．
14. 如图，在平行四边形ABCD中， ， CE平分交AD边于点E，且 ， 则BC的长为 ．
15. 如图，等腰梯形ABCD中，ADBC，对角线AC⊥BD，若AD＝2，BC＝4，则该梯形的面积为 ．
16. 如图，在矩形ABCD中，AC，BD相交于点O，AE平分∠BAD交BC于点E，若∠CAE＝15°，则∠BOE的度数为 ．
17. 如图，在四边形ABCD中，E、F、G、H分别是AB、BD、CD、AC的中点，要使四边形EFGH是菱形，四边形ABCD还应满足的一个条件是 ．
18. 如图，将边长为2cm的正方形ABCD沿其对角线AC剪开，再把ABC沿着AD方向平移，得到 ， 若两个三角形重叠部分的面积是1cm2 ， 则它移动的距离等于cm．
三、解答题
-
19. 已知一次函数的图象与直线y＝﹣2x+3平行，且与直线y＝4x﹣5交于点(2，m)．求此一次函数的解析式．20. 如图，在梯形ABCD中，AD∥BC，∠B=45°，AD=8，AB= ， CD=26，求BC的长．
21. 已知，如图，在 中，分别在边 上取两点，使得 ，连接 相交于点 ，若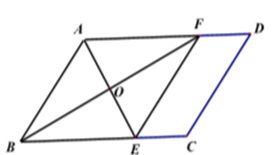
(1)、求证：四边形 是菱形； .(2)、若菱形 的周长为 求 的长.22. 甲、乙两人从学校出发，甲先出发，乙后出发，都匀速骑车前往图书馆，乙在骑行途中休息片刻后，以原速度继续骑行．已知乙的速度是甲的1.6倍，甲、乙两人离学校的距离y（米）与乙行驶的时间x（分钟）之间的关系如图，请根据图象回答问题．
(1)、乙骑行的速度是米/分钟；甲骑行的速度是米/分钟；(2)、甲比乙先出发分钟；(3)、求线段BD所表示的y与x之间的函数解析式．23. 如图，在▱ABCD 中，对角线 AC 与 BD 相交于点 O ，点 E ， F 分别为 OB ， OD 的中点，延长 AE 至 G ，使 EG ＝AE ，连接 CG ．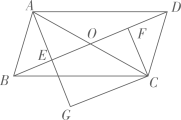
(1)、求证： △ABE≌△CDF ；(2)、当 AB 与 AC 满足什么数量关系时，四边形 EGCF 是矩形？请说明理由.24. 如图，在平面直角坐标系xOy中，已知直线AQ与x轴负半轴交于点A，与y轴正半轴交于点Q，∠QAO＝45°，直线AQ在y轴上的截距为2，直线BE：y＝﹣2x+8与直线AQ交于点P．
(1)、求直线AQ的表达式；(2)、在y轴上取一点F，当四边形BPFO为是梯形时，求点F的坐标；(3)、点D为直角坐标平面内一点，如果以Q、P、B、D为顶点的四边形是平行四边形，请直接写出点D的坐标．25. 如图，E是正方形ABCD的边AD上的动点，F是边BC延长线上的一点，且BF=EF，AB=12，设AE=x，BF=y．
(1)、当△BEF是等边三角形时，求BF的长；(2)、求y与x的函数解析式，并写出它的定义域；(3)、把△ABE沿着直线BE翻折，点A落在点A′处，试探索：△A′BF能否为等腰三角形？如果能，请求出AE的长；如果不能，请说明理由．