辽宁省沈阳市沈河区2020-2021学年八年级下学期期中数学试题
试卷更新日期:2022-03-10 类型:期中考试
一、单选题
-
1. 已知a>b,下列变形一定正确的是( )A、3a<3b B、4+a>4﹣b C、ac3>bc3 D、3+2b>3+2b2. 下列用数轴表示不等式组 的解集正确的是( )A、
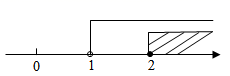 B、
B、 C、
C、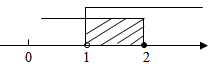 D、
D、 3. 如图,平移△ABC得到△DEF , 其中点A的对应点是点D , 则下列结论中不成立的是( )
3. 如图,平移△ABC得到△DEF , 其中点A的对应点是点D , 则下列结论中不成立的是( ) A、AD∥BE B、∠BAC=∠DFE C、AC=DF D、∠ABC=∠DEF4. 如图,A,B 两点被池塘隔开,在 AB 外选一点 C,连接 AC,BC,分别取 AC,BC 的中点D,E,连接 DE.若测得 DE=5,则 AB 的长为( ).
A、AD∥BE B、∠BAC=∠DFE C、AC=DF D、∠ABC=∠DEF4. 如图,A,B 两点被池塘隔开,在 AB 外选一点 C,连接 AC,BC,分别取 AC,BC 的中点D,E,连接 DE.若测得 DE=5,则 AB 的长为( ). A、5 B、8 C、10 D、无法确定5. 如图,AC,BD相交于点O,∠A=∠D,如果请你再补充一个条件,使得△BOC是等腰三角形,那么你补充的条件不能是( )
A、5 B、8 C、10 D、无法确定5. 如图,AC,BD相交于点O,∠A=∠D,如果请你再补充一个条件,使得△BOC是等腰三角形,那么你补充的条件不能是( )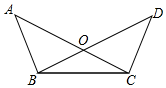 A、OA=OD B、AB=CD C、∠ABO=∠DCO D、∠ABC=∠DCB6. 下列不能判定四边形是平行四边形的条件是( )
A、OA=OD B、AB=CD C、∠ABO=∠DCO D、∠ABC=∠DCB6. 下列不能判定四边形是平行四边形的条件是( )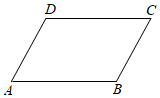 A、∠A=∠C,∠B=∠D B、AB∥CD,AD∥BC C、AB∥CD,AD=BC D、AB=CD,AD=BC7.
A、∠A=∠C,∠B=∠D B、AB∥CD,AD∥BC C、AB∥CD,AD=BC D、AB=CD,AD=BC7.如图,直线l1∥l2 , 以直线l1上的点A为圆心、适当长为半径画弧,分别交直线l1、l2于点B、C,连接AC、BC.若∠ABC=67°,则∠1=( )
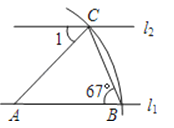 A、23° B、46° C、67° D、78°8. 在中, , 两个完全一样的三角尺按如图所示摆放.它们一组较短的直角边分别在 , 上,另一组较长的对应边的顶点重合于点P,交边于点D,则下列结论不正确的是( )
A、23° B、46° C、67° D、78°8. 在中, , 两个完全一样的三角尺按如图所示摆放.它们一组较短的直角边分别在 , 上,另一组较长的对应边的顶点重合于点P,交边于点D,则下列结论不正确的是( )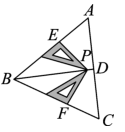 A、平分 B、 C、垂直平分 D、9. 如图,点D是△ABC外的一点,BD,CD分别平分外角∠CBE与∠BCF,连接AD交BC于点O.下列结论一定成立的是( )
A、平分 B、 C、垂直平分 D、9. 如图,点D是△ABC外的一点,BD,CD分别平分外角∠CBE与∠BCF,连接AD交BC于点O.下列结论一定成立的是( )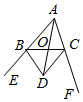 A、DB=DC B、OA=OD C、∠BDA=∠CDA D、∠BAD=∠CAD10. 如图,直线y1=x+b与y2=kx﹣1相交于点P,若点P的横坐标为﹣1,则关于x的不等式x+b≥kx﹣1的解集是( )
A、DB=DC B、OA=OD C、∠BDA=∠CDA D、∠BAD=∠CAD10. 如图,直线y1=x+b与y2=kx﹣1相交于点P,若点P的横坐标为﹣1,则关于x的不等式x+b≥kx﹣1的解集是( )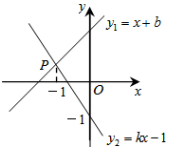 A、x≥﹣1 B、x>﹣1 C、x≤﹣1 D、x<﹣1
A、x≥﹣1 B、x>﹣1 C、x≤﹣1 D、x<﹣1二、填空题
-
11. 3x﹣7≤2的解集是 .12. 如图,将△ABC绕点 旋转到△AEF的位置,点E在BC边上,EF与AC交于点G.若∠B=70°,∠C=25°,则∠FGC=°.
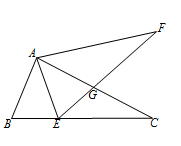 13. 如图,在平行四边形ABCD中,BE⊥CD,BF⊥AD,垂足分别为E,F,CE=2,DF=1,∠EBF=60°,则平行四边形ABCD的周长为.
13. 如图,在平行四边形ABCD中,BE⊥CD,BF⊥AD,垂足分别为E,F,CE=2,DF=1,∠EBF=60°,则平行四边形ABCD的周长为.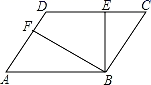 14. 如图,▱ABCD的对角线AC与BD交于点O,BD⊥AD,AB=10,AD=6,则AC的长为.
14. 如图,▱ABCD的对角线AC与BD交于点O,BD⊥AD,AB=10,AD=6,则AC的长为.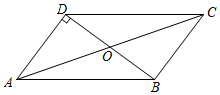 15. 某商场出售某种小家电商品,标价为360元,比进价高出80%,为了吸引顾客,又进行降价处理,若要使售后利润率不低于20%(利润率=×100%),则这种小家电最多可降价元.16. 如图,D是等边三角形ABC外一点,AD=3,CD=2,当BD长最大时,△ABC的面积为 .
15. 某商场出售某种小家电商品,标价为360元,比进价高出80%,为了吸引顾客,又进行降价处理,若要使售后利润率不低于20%(利润率=×100%),则这种小家电最多可降价元.16. 如图,D是等边三角形ABC外一点,AD=3,CD=2,当BD长最大时,△ABC的面积为 .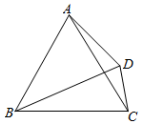
三、解答题
-
17. 下面是小颍同学解一元一次不等式的过程,请认真阅读并完成相应的任务.
解不等式组: .
解:去分母,得2(x+2)﹣6<3(2x﹣1)……第一步
去括号,得2x+4﹣6<6x﹣3.……第二步
移项,合并同类项,得﹣4x<﹣1.……第三步
两边同时除以﹣4,得x<﹣……第四步
(1)、上述过程中,第一步的依据是 ;第 步出现错误;(2)、该不等式的解集应为 .18. 利用数轴求出不等式组的解集.19. 如图,作法,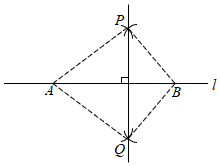
已知直线l和l外一点P,下面是小明设计的“过点P作直线的垂线”的作法:
请结合图形阅读作法,并将证明“PQ⊥l”的过程补充完整.
作法:①在直线上取点A,B;
②分别以点A、B为圆心,AP、BP为半径作弧,两弧在直线l下方交于点Q;
③作直线PQ.
结论:PQ⊥l,且PQ经过点P.
证明:连接AP,AQ,BP,BQ.
由作法可知,AP=AQ,BP=BQ.
∴点A在线段PQ的垂直平分线上,点B在线段PQ的垂直平分线上,(依据 )
∴直线AB是线段PQ的垂直平分线(依据: )
∴PQ⊥l.
20. 按要求画图及填空:在由边长为1个单位长度的小正方形组成的网格中建立如图所示平面直角坐标系,原点O及△ABC的顶点都在格点上.
( 1 )图中线段AB的长度为 ;
( 2 )将△ABC先向下平移2个单位长度,再向右平移5个单位长度得到△A1B1C1 , 画出△A1B1C1;
( 3 )将△ABC绕点B逆时针旋转90°,画出旋转后得到的△A2B2C2 , 直接写出点A2、C2的坐标.
21. 在△ABC中,∠B+∠ACB=30°,AB=4,△ABC逆时针旋转一定角度后与△ADE重合,且点C恰好成为AD中点,如图.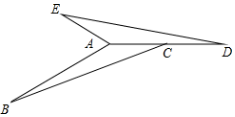 (1)、旋转中心是 , 旋转角的大小是 .(2)、求出∠BAE的度数和AE的长.22. 如图,在四边形ABCD中,E、F、G、H分别是AB、CD、AC、BD的中点.
(1)、旋转中心是 , 旋转角的大小是 .(2)、求出∠BAE的度数和AE的长.22. 如图,在四边形ABCD中,E、F、G、H分别是AB、CD、AC、BD的中点.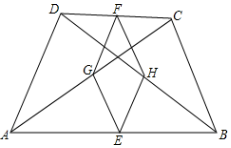 (1)、求证:四边形EGFH是平行四边形;(2)、若AD=8,则GF= .23. 某工厂要招聘A,B两个工种的工人180人,A,B两个工种的工人的月工资分别为2000元和3000元.现要求B工种的人数不少于A工种人数的2倍.(1)、该工厂招聘A种工人最多多少人?(2)、招聘A工种工人多少人时,可使每月所付的工资总额最少,最少为多少元.24. 如图,在平行四边形纸片ABCD中,AD=6cm,将纸片沿对角线BD对折,边AB的对应边BF与CD边交于点E,此时△BCE恰为等边三角形.
(1)、求证:四边形EGFH是平行四边形;(2)、若AD=8,则GF= .23. 某工厂要招聘A,B两个工种的工人180人,A,B两个工种的工人的月工资分别为2000元和3000元.现要求B工种的人数不少于A工种人数的2倍.(1)、该工厂招聘A种工人最多多少人?(2)、招聘A工种工人多少人时,可使每月所付的工资总额最少,最少为多少元.24. 如图,在平行四边形纸片ABCD中,AD=6cm,将纸片沿对角线BD对折,边AB的对应边BF与CD边交于点E,此时△BCE恰为等边三角形.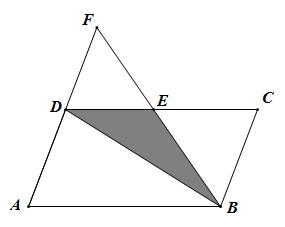 (1)、求AB的长度;(2)、重叠部分的面积为 ;(3)、将线段BC沿射线BA方向移动,平移后的线段记作B'C',请直接写出B'F+C'F的最小值.25. 已知:△ABC,△CDE中,∠ACB=∠DCE=90°,AC=BC=6,CD=CE=4,△CDE可以绕点C旋转,作直线AD、直线BE,当它们有交点时.设相交点为H.
(1)、求AB的长度;(2)、重叠部分的面积为 ;(3)、将线段BC沿射线BA方向移动,平移后的线段记作B'C',请直接写出B'F+C'F的最小值.25. 已知:△ABC,△CDE中,∠ACB=∠DCE=90°,AC=BC=6,CD=CE=4,△CDE可以绕点C旋转,作直线AD、直线BE,当它们有交点时.设相交点为H.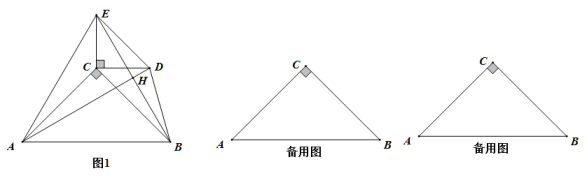 (1)、当△CDE转到图1位置时,求证:①AD=BE;②AD⊥BE;(2)、△CDE可以绕点C旋转的过程中,连接AE,BD.猜想AE2+BD2的值是否发生变化(直接写出结论,不用证明)?直接写出当BD=8时,AE的长;(3)、△CDE可以绕点C旋转的过程中,直接写出当∠CBD=30°时,AE2的值.
(1)、当△CDE转到图1位置时,求证:①AD=BE;②AD⊥BE;(2)、△CDE可以绕点C旋转的过程中,连接AE,BD.猜想AE2+BD2的值是否发生变化(直接写出结论,不用证明)?直接写出当BD=8时,AE的长;(3)、△CDE可以绕点C旋转的过程中,直接写出当∠CBD=30°时,AE2的值.