辽宁省盘锦市大洼区2020-2021学年八年级下学期期中数学试题
试卷更新日期:2022-03-10 类型:期中考试
一、单选题
-
1. 下列二次根式中属于最简二次根式的是( )A、 B、 C、 D、2. 如果x是任意实数,下列各式中一定有意义的是( )A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、= D、4. 在以下列线段a、b、c的长为边的三角形中,不能构成直角三角形的是( )A、a=9 b=41 c=40 B、a=b=5 c=5 C、a:b:c=3:4:5 D、a=11 b=12 c=155. 如图,两张对边平行且等宽的纸条交叉叠放在一起,重合部分构成的四边形ABCD是( )
 A、平行四边形 B、菱形 C、矩形 D、正方形6. 下列命题中,真命题是( )A、对角线相等的四边形是矩形 B、对角线互相垂直的四边形是菱形 C、对角线互相平分的四边形是平行四边形 D、对角线互相垂直平分的四边形是正方形7. 正方形具备而菱形不具备的性质是()A、对角线互相平分 B、对角线互相垂直 C、对角线相等 D、每条对角线平分一组对角8. 如图,数轴上点A、B分别对应1、2,过点B作PQ⊥AB,以B为圆心,AB长为半径画弧,交PQ于点C,以原点O为圆心,OC长为半径画弧,交数轴于点M,则点M对应的数是( )
A、平行四边形 B、菱形 C、矩形 D、正方形6. 下列命题中,真命题是( )A、对角线相等的四边形是矩形 B、对角线互相垂直的四边形是菱形 C、对角线互相平分的四边形是平行四边形 D、对角线互相垂直平分的四边形是正方形7. 正方形具备而菱形不具备的性质是()A、对角线互相平分 B、对角线互相垂直 C、对角线相等 D、每条对角线平分一组对角8. 如图,数轴上点A、B分别对应1、2,过点B作PQ⊥AB,以B为圆心,AB长为半径画弧,交PQ于点C,以原点O为圆心,OC长为半径画弧,交数轴于点M,则点M对应的数是( )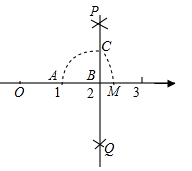 A、 B、 C、2 D、9. 如图,在Rt△ABC中,∠ACB=90°,点D是AB的中点,且CD= , 如果Rt△ABC的面积为1,则它的周长为( )
A、 B、 C、2 D、9. 如图,在Rt△ABC中,∠ACB=90°,点D是AB的中点,且CD= , 如果Rt△ABC的面积为1,则它的周长为( )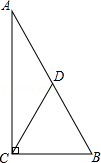 A、 B、+1 C、+2 D、+310. 如图,正方形ABCD的边长为4,点E在对角线BD上,且 ,EF⊥AB,垂足为F,则EF的长为
A、 B、+1 C、+2 D、+310. 如图,正方形ABCD的边长为4,点E在对角线BD上,且 ,EF⊥AB,垂足为F,则EF的长为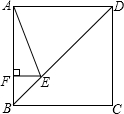 A、1 B、 C、 D、
A、1 B、 C、 D、二、填空题
-
11. 计算:=12. 计算的值等于 .13. 如图,以△ABC的三边为边向外作正方形,其面积分别为S1 , S2 , S3 , 且S1=9,S3=25,当S2=时∠ACB=90°.
 14. 如图所示,在Rt△ABC中,∠ACB=90°,CM是斜边AB的中线,E、F分别为BM、BC的中点,若EF=1,则AB= .
14. 如图所示,在Rt△ABC中,∠ACB=90°,CM是斜边AB的中线,E、F分别为BM、BC的中点,若EF=1,则AB= . 15. 在矩形ABCD中,M,N,P,Q分别为边AB,BC,CD,DA上的点(不与端点重合).对于任意矩形ABCD,下面四个结论中,①存在无数个四边形MNPQ是平行四边形;②存在无数个四边形MNPQ是矩形;③存在无数个四边形MNPQ是菱形;④至少存在一个四边形MNPQ是正方形.所有正确结论的序号是 .16. 如图,在菱形ABCD中,AB∥y轴,且B(-3,1),C(1,4),则点A的坐标为 .
15. 在矩形ABCD中,M,N,P,Q分别为边AB,BC,CD,DA上的点(不与端点重合).对于任意矩形ABCD,下面四个结论中,①存在无数个四边形MNPQ是平行四边形;②存在无数个四边形MNPQ是矩形;③存在无数个四边形MNPQ是菱形;④至少存在一个四边形MNPQ是正方形.所有正确结论的序号是 .16. 如图,在菱形ABCD中,AB∥y轴,且B(-3,1),C(1,4),则点A的坐标为 . 17. 如图,把一个等腰直角△ABC纸片沿斜边上的高CD(裁剪线)剪一刀,再把剪得的三角形纸片与剩下的部分重新拼接,能拼成的特殊四边形是 .
17. 如图,把一个等腰直角△ABC纸片沿斜边上的高CD(裁剪线)剪一刀,再把剪得的三角形纸片与剩下的部分重新拼接,能拼成的特殊四边形是 . 18. 如图,矩形ABCD中, ,点E是BC边上一点,连接AE,把 沿AE折叠,使点B落在点 处 当 为直角三角形时,BE的长为 .
18. 如图,矩形ABCD中, ,点E是BC边上一点,连接AE,把 沿AE折叠,使点B落在点 处 当 为直角三角形时,BE的长为 .
三、解答题
-
19. 计算: .20. 计算: .21. 已知 , 求代数式的值.22. 在B港有甲、乙两艘渔船,若甲船沿北偏东60°的方向以每小时8海里的速度前进,乙船沿南偏东某个角度的方向以每小时15海里的速度前进,2小时后,甲船到M岛,乙船到P岛,两岛相距34海里,你知道乙船是沿哪个方向航行的吗?23. 如图,四边形 是菱形, ,垂足分别为点 .
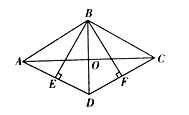 (1)、求证: ;(2)、当菱形 的对角线 ,BD=6时,求 的长.24. 如图在平面直角坐标系中,点A(-2,0),B(2,3),C(0,4).
(1)、求证: ;(2)、当菱形 的对角线 ,BD=6时,求 的长.24. 如图在平面直角坐标系中,点A(-2,0),B(2,3),C(0,4). (1)、判断△ABC的形状,并说明理由;(2)、点D为平面直角坐标系中的点,以A、B、C、D为顶点的四边形为平行四边形,写出所有满足条件的点D的坐标.25. 如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC交直线MN于点E,垂足为F,连接CD,BE.
(1)、判断△ABC的形状,并说明理由;(2)、点D为平面直角坐标系中的点,以A、B、C、D为顶点的四边形为平行四边形,写出所有满足条件的点D的坐标.25. 如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC交直线MN于点E,垂足为F,连接CD,BE. (1)、求证:CE=AD;(2)、当D为AB中点时,四边形BECD是什么特殊四边形?请说明理由;(3)、若D为AB中点,则当∠A等于多少度时,四边形BECD是正方形?请说明理由.26. 如图,四边形ABCD是正方形,点E、F分别在边BC、AB上,点G在边BA的延长线上,且CE=BF=AG.
(1)、求证:CE=AD;(2)、当D为AB中点时,四边形BECD是什么特殊四边形?请说明理由;(3)、若D为AB中点,则当∠A等于多少度时,四边形BECD是正方形?请说明理由.26. 如图,四边形ABCD是正方形,点E、F分别在边BC、AB上,点G在边BA的延长线上,且CE=BF=AG.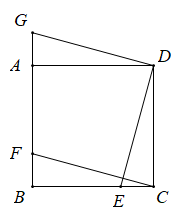 (1)、求证:①DE=DG ;②DE⊥DG;(2)、尺规作图:以线段DE、DG为边作出正方形DEHG(保留作图痕迹不写作法和证明);(3)、连接(2)中的FH,猜想四边形CEHF的形状,并证明你的猜想;(4)、当时,求出的值.27. 如图,△ABC中,点O是边AC上一动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)、求证:①DE=DG ;②DE⊥DG;(2)、尺规作图:以线段DE、DG为边作出正方形DEHG(保留作图痕迹不写作法和证明);(3)、连接(2)中的FH,猜想四边形CEHF的形状,并证明你的猜想;(4)、当时,求出的值.27. 如图,△ABC中,点O是边AC上一动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F. (1)、当点O在边AC上运动到什么位置时,四边形AECF为矩形?并说明理由;(2)、在(1)的条件下,△ABC满足什么条件时,四边形AECF是正方形?说明理由.
(1)、当点O在边AC上运动到什么位置时,四边形AECF为矩形?并说明理由;(2)、在(1)的条件下,△ABC满足什么条件时,四边形AECF是正方形?说明理由.