辽宁省抚顺市新宾满族自治县2020-2021学年八年级下学期期中数学试题
试卷更新日期:2022-03-10 类型:期中考试
一、单选题
-
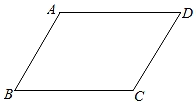
1. 下列二次根式中,是最简二次根式的是( )A、 B、 C、 D、2. 式子在实数范围内有意义,则x的取值范围是( )A、x≥0 B、x≥1 C、x≥﹣1 D、x≤﹣13. 下列计算正确的是( )A、 B、 C、 D、4. 下列说法正确的是( )A、对角线互相垂直的四边形是菱形 B、矩形的对角线互相垂直 C、一组对边平行的四边形是平行四边形 D、对角线相等的平行四边形是矩形5. 如图,在平行四边形ABCD中,∠B+∠D=100°,则∠A等于( )
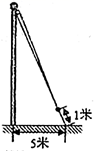
 A、50° B、65° C、100° D、130°6. 如图,为了测算出学校旗杆的高度,小明将升旗的绳子拉到旗杆底端,并在与旗杆等长的地方打了一个结,然后将绳子底端拉到离旗杆底端5米的地面某处,发现此时绳子底端距离打结处约1米,则旗杆的高度是( )
A、50° B、65° C、100° D、130°6. 如图,为了测算出学校旗杆的高度,小明将升旗的绳子拉到旗杆底端,并在与旗杆等长的地方打了一个结,然后将绳子底端拉到离旗杆底端5米的地面某处,发现此时绳子底端距离打结处约1米,则旗杆的高度是( )
 A、12 B、13 C、15 D、247. 若菱形的两条对角线长分别是6和8,则它的周长为( )A、20 B、24 C、40 D、488. 如图,在平行四边形 中, 平分 ,交 于点 , 平分 交 于点 , , ,则 长为( )
A、12 B、13 C、15 D、247. 若菱形的两条对角线长分别是6和8,则它的周长为( )A、20 B、24 C、40 D、488. 如图,在平行四边形 中, 平分 ,交 于点 , 平分 交 于点 , , ,则 长为( ) A、1 B、2 C、3 D、49. 如图,四边形ABCD为菱形,对角线AC,BD相交于点O,DH⊥AB于点H,连接OH,∠CAD=25°,则∠DHO的度数是( )
A、1 B、2 C、3 D、49. 如图,四边形ABCD为菱形,对角线AC,BD相交于点O,DH⊥AB于点H,连接OH,∠CAD=25°,则∠DHO的度数是( )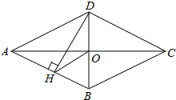 A、20° B、25° C、30° D、35°10. 如图,在▱ABCD中,AD=2AB , F是AD的中点,作CE⊥AB , 垂足E在线段AB上,连接EF、CF , 下列结论中:①∠DCF= ∠BCD;②∠DFE=3∠AEF;③EF=CF;④S△BEC=S△CEF . 一定成立的是( )
A、20° B、25° C、30° D、35°10. 如图,在▱ABCD中,AD=2AB , F是AD的中点,作CE⊥AB , 垂足E在线段AB上,连接EF、CF , 下列结论中:①∠DCF= ∠BCD;②∠DFE=3∠AEF;③EF=CF;④S△BEC=S△CEF . 一定成立的是( ) A、①②③④ B、①②③ C、①②④ D、①③④
A、①②③④ B、①②③ C、①②④ D、①③④二、填空题
-
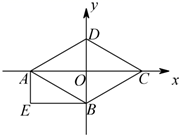
11. = .12. 平面直角坐标系中,点到原点的距离是 .13. 若 , 时,则 的值是.14. 如图,四边形 为菱形,四边形 为矩形, , , 三点的坐标为 , , ,则点 的坐标为.
 15. 如图,E为▱ABCD的边AD上任意一点,▱ABCD的面积为6,则图中阴影部分的面积为 .
15. 如图,E为▱ABCD的边AD上任意一点,▱ABCD的面积为6,则图中阴影部分的面积为 .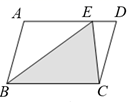 16. 如图是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC,DE垂直于横梁AC,AB=8m,∠ABC=60°,则DE=m.
16. 如图是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC,DE垂直于横梁AC,AB=8m,∠ABC=60°,则DE=m. 17. 如图,在平行四边形ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD'E处,AD'与CE交于点F.若∠B=54°,∠DAE=20°,则∠FED'的大小为°.
17. 如图,在平行四边形ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD'E处,AD'与CE交于点F.若∠B=54°,∠DAE=20°,则∠FED'的大小为°. 18. 如图▱ABCD中,AC与BD交于点O,BD=2AD,E,F,G分别是OC,OD,AB的中点,下列结论:①FE=GE;②FE⊥GE;③∠ADB=2∠CBE;④GF平分∠AGE, 其中正确的有 .
18. 如图▱ABCD中,AC与BD交于点O,BD=2AD,E,F,G分别是OC,OD,AB的中点,下列结论:①FE=GE;②FE⊥GE;③∠ADB=2∠CBE;④GF平分∠AGE, 其中正确的有 .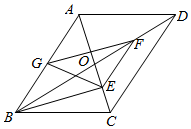
三、解答题
-
19. 计算:(1)、;(2)、;(3)、;(4)、 .20. 已知 , , 求a2+b2﹣3ab的值.21. 如图,正方形ABCD的对角线AC、BD相交于点O,E、F分别在OB、OC上,OE=OF.求证:AE=BF.
 22. 为了绿化环境,我县某中学有一块四边形的空地ABCD,如图所示,学校计划在空地上种植草皮,经测量,∠ADC=90°,CD=3米,AD=4米,AB=13米,BC=12米.
22. 为了绿化环境,我县某中学有一块四边形的空地ABCD,如图所示,学校计划在空地上种植草皮,经测量,∠ADC=90°,CD=3米,AD=4米,AB=13米,BC=12米. (1)、求出空地ABCD的面积.(2)、若每种植1平方米草皮需要300元,问总共需投入多少元?23. 如图,D、E、F分别是△ABC三边中点,AH⊥BC于H.
(1)、求出空地ABCD的面积.(2)、若每种植1平方米草皮需要300元,问总共需投入多少元?23. 如图,D、E、F分别是△ABC三边中点,AH⊥BC于H.
求证:
(1)、∠BDF=∠BAC;(2)、DF=EH.