辽宁省抚顺市抚顺县2020-2021学年八年级下学期期中数学试题
试卷更新日期:2022-03-10 类型:期中考试
一、单选题
-
1. 使式子无意义的x的取值范围是( )A、 B、 C、 D、2. 下列四组线段不能围成直角三角形的是( )A、a=8,b=15,c=17 B、a=9,b=12,c=15 C、 , , D、a︰b︰c=2︰3︰43. 下列命题中,不正确的是( )A、直角三角形斜边中线等于斜边的一半 B、平行四边形的对角线互相平分且相等 C、矩形的对角线相等 D、菱形的两条对角线互相垂直4. 如图,在中的对角线 , 相交于点O,且 , , 则的周长( )
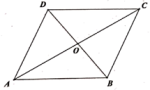 A、10 B、14 C、20 D、225. 如图,点E在正方形内,满足 , , , 则阴影部分的面积是( )
A、10 B、14 C、20 D、225. 如图,点E在正方形内,满足 , , , 则阴影部分的面积是( )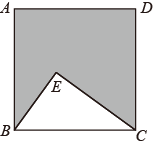 A、48 B、60 C、76 D、806. 下列计算中,正确的是( )A、 B、 C、 D、7. 若 ,则 的值为( )A、1 B、-1 C、-7 D、78. 如图,在数轴上点A表示 , 过点A作数轴的垂线截取 , 以原点O为圆心,以长为半径画弧,交负半轴于点C,那么点C所表示的数是( )
A、48 B、60 C、76 D、806. 下列计算中,正确的是( )A、 B、 C、 D、7. 若 ,则 的值为( )A、1 B、-1 C、-7 D、78. 如图,在数轴上点A表示 , 过点A作数轴的垂线截取 , 以原点O为圆心,以长为半径画弧,交负半轴于点C,那么点C所表示的数是( )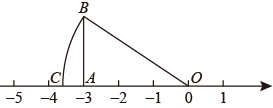 A、 B、 C、 D、9. 如图,在中, , , , 是斜边边上的中线,则的长是( )
A、 B、 C、 D、9. 如图,在中, , , , 是斜边边上的中线,则的长是( ) A、5 B、6 C、 D、10. 如图,在矩形ABCD中,P、Q分别是BC、DC上的点,E,F分别是AP、PQ的中点.BC=12, DQ =5,在点P从B移动到C(点Q不动)的过程中,则下列结论正确的是 ( )
A、5 B、6 C、 D、10. 如图,在矩形ABCD中,P、Q分别是BC、DC上的点,E,F分别是AP、PQ的中点.BC=12, DQ =5,在点P从B移动到C(点Q不动)的过程中,则下列结论正确的是 ( )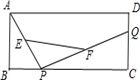 A、线段EF的长逐渐增大,最大值是13 B、线段EF的长逐渐减小,最小值是6.5 C、线段EF的长始终是6.5 D、线段EF的长先增大再减小,且6.5≤EF≤13
A、线段EF的长逐渐增大,最大值是13 B、线段EF的长逐渐减小,最小值是6.5 C、线段EF的长始终是6.5 D、线段EF的长先增大再减小,且6.5≤EF≤13二、填空题
-
11. 计算: = .12. 一个直角三角形的两边长为3和4,则这个三角形的最长边是 .13. 已知 , 化简: .14. 如果 , 那么x15. 如图所示,是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A,B,C,D的边长分别是2,4,1,2,最大正方形E的面积是 .
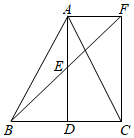
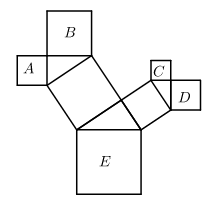 16. 如图所示,的对角线与相交于点O,交于E,若 , 的周长等于4.5,则的周长为 .
16. 如图所示,的对角线与相交于点O,交于E,若 , 的周长等于4.5,则的周长为 .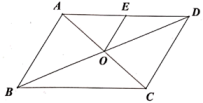 17. 如图,矩形纸片ABCD中,已知AD=8,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为 .
17. 如图,矩形纸片ABCD中,已知AD=8,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为 .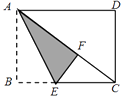 18. 如图,是以的对角线为边的等边三角形,点C与点E关于轴对称,若E点的坐标为 , 则D点的坐标是 .
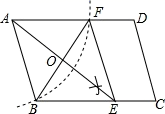
18. 如图,是以的对角线为边的等边三角形,点C与点E关于轴对称,若E点的坐标为 , 则D点的坐标是 .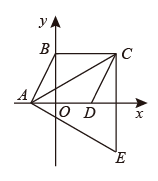
三、解答题
-
19. 计算:(1)、(2)、(3)、已知 , , 求代数式的值.20. 如图,在每个小正方形边长均为1个单位长度的方格纸中,画出了 , , , 四条线段.
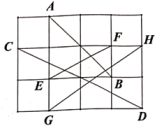 (1)、分别求出四条线段 , , , 的长度;(2)、在上面四条线段中,哪三条线段能构成一个直角三角形?并说明理由.21. 观察下列各式及其验证过程: , , , …
(1)、分别求出四条线段 , , , 的长度;(2)、在上面四条线段中,哪三条线段能构成一个直角三角形?并说明理由.21. 观察下列各式及其验证过程: , , , …验证:;
(1)、请仿照上面的方法来验证;(2)、根据上面反映的规律,请将猜到的规律用含自然数的代数式表示出来.22. 如图,中, , , .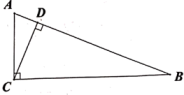 (1)、求斜边的长;(2)、求高的长.23. 如图,矩形 中, 的平分线交 于点E,O为对角线 和 交点,且 .
(1)、求斜边的长;(2)、求高的长.23. 如图,矩形 中, 的平分线交 于点E,O为对角线 和 交点,且 .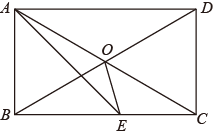 (1)、证明 为等边三角形;(2)、求 的度数.24. 如图,已知△ABC是等边三角形,点D,F分别在线段BC,AB上,∠EFB=60°,EF=DC.
(1)、证明 为等边三角形;(2)、求 的度数.24. 如图,已知△ABC是等边三角形,点D,F分别在线段BC,AB上,∠EFB=60°,EF=DC. (1)、求证:四边形EFCD是平行四边形.(2)、若BE=EF,求证:AE=AD.
(1)、求证:四边形EFCD是平行四边形.(2)、若BE=EF,求证:AE=AD.