辽宁省大连市中山区2020-2021学年八年级下学期期中数学试题

试卷更新日期：2022-03-10 类型：期中考试

进入出卷网下载

一、单选题

1. 使式子 $\sqrt{a - 2}$ 有意义的a的取值范围是（）

A、 $a > 2$ B、 $a \geq 2$ C、 $a \neq 2$ D、 $a \leq 2$

查看试题解析
2. 下列选项中，运算正确的是（）

A、 $4 \sqrt{3} - \sqrt{3} = 4$ B、 $\sqrt{3} + \sqrt{3} = 3$ C、 $\sqrt{3} \cdot \sqrt{2} = \sqrt{6}$ D、 $\sqrt{12} \div \sqrt{6} = 2$

查看试题解析
3. 若函数y=kx的图象经过点（-1，2），则k的值是（）

A、 $- 2$ B、2 C、 $- \frac{1}{2}$ D、 $\frac{1}{2}$

查看试题解析
4. 如图，要使 $▱ A B C D$ 成为矩形，需添加的条件是（）

A、 $A B = B C$ B、 $A C ⊥ B D$ C、 $∠ A B C = 90 °$ D、 $∠ A B D = ∠ C B D$

查看试题解析
5. 如图，在平面直角坐标系中，A（﹣1，0），B（0，2），以点A为圆心，AB为半径画弧，交x轴正半轴于点C，点C的横坐标介于（　　）

A、0到1之间 B、1到2之间 C、2到3之间 D、3到4之间

查看试题解析
6. 如图，在△ABC中，∠A=∠B=45 $°$ ，AB=4，以AC为边的阴影部分图形是一个正方形，则这个正方形的面积为（）

A、2 B、4 C、8 D、16

查看试题解析
7. 一次函数 $y = 3 x - 2$ 的图像不经过的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
8. 如图，在▱ABCD中，AE平分∠BAD，交CD边于E，AD=3，EC=2，则DC的长为（）

A、1 B、2 C、3 D、5

查看试题解析
9. 下列属于菱形性质的是（）

A、对角线相等 B、对角线互相垂直 C、对角互补 D、四个角都是直角

查看试题解析
10. 小明步行从家出发去学校，步行了5分钟时，发现作业忘在家，马上以同样的速度回家取作业，然后骑共享单车赶往学校，小明离家距离S（米）与时间t（分钟）之间的函数图象如图，则小明骑车比步行的速度每分钟快（）

A、200 B、80 C、140 D、120

查看试题解析

二、填空题

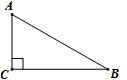
11. 如图，在 $R t △ A B C$ 中，∠C=90°，∠B=30°，AC=3，则AB= ．

查看试题解析
12. 计算 $(\sqrt{3} - 2) (\sqrt{3} + 2)$ 的结果等于．

查看试题解析
13. 直线l过点A（1，0）且与直线y=-3x+6平行，则l的解析式为．

查看试题解析
14. 如图，DE是△ABC的中位线，若BC的长是4cm，则DE的长是cm．

查看试题解析
15. 菱形ABCD中，已知AB＝4，∠B＝60°，那么BD的长是．

查看试题解析
16. 在平面直角坐标中，已知点 $P (1 ， 2)$ ， $Q (4 ， 10)$ ，直线 $y = k x + k (k \neq 0)$ 与线段 $P Q$ 有交点，则k的取值范围为．

查看试题解析

三、解答题

17. 计算：

(1)、 $2 \sqrt{12} + 6 \sqrt{\frac{1}{3}} - \sqrt{48}$

(2)、 $(4 \sqrt{2} - \sqrt{6}) \div \sqrt{2}$

查看试题解析
18. 如图，▱ABDC中，E，F是对角线BC上两点，且BF=CE.求证AF∥DE.

查看试题解析
19. 如图， $△ A B C$ 中， $A B = A C = B C = 6$ ，求高 $A D$ 的长．

查看试题解析
20. 已知一次函数y=kx-2（k≠0）的图象过点M．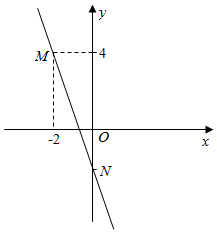

(1)、求实数k的值；

(2)、设一次函数y=kx-2（k≠0）的图象与y轴交于点N．求△MON的面积．

查看试题解析
21. 如图，在平行四边形ABCD中，对角线AC，BD相交于点　O，且OA=OD，∠OAD=50°．求∠OAB的度数．

查看试题解析
22. 在平面直角坐标系xOy中，点A的坐标为（6，0），点P（x，y）在第一象限，且x+y=8．设△OPA的面积为S．用含x的式子表示S，并写出x的取值范围．

查看试题解析
23. 如图，某港口P位于东西方向的海岸线上．“远航”号、“海天”号轮船同时离开港口，各自沿一固定方向航行，“远航”号每小时航行16海里，“海天”号每小时航行12海里．它们离开港口一个半小时后分别位于点Q，R处，且相距30海里．如果知道“远航”号沿东北方向航行，能知道“海天”号沿哪个方向航行吗？

查看试题解析
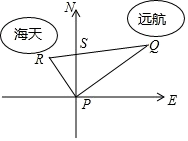24. 五一假期小明和小强分别从家出发去公园，小明比小强先出发 $2 m i n$ ，俩人同时到达公园，小明的速度为 $80 m / m i n$ ，设小明、小强两人相距 $y m$ 与小明行进行的时间 $x m i n$ 之间的函数关系如图所示：

(1)、填空：小明和小强家相距m，a=；

(2)、求线段AB对应的函数表达式，并直接写出自变量x的取值范围．

(3)、设小强离家的距离为 $y_{1} m$ ，小明行进的时间 $x m i n$ ，求 $y_{1}$ 与x的函数关系式，并画出函数的图象．

查看试题解析
25. 如图，四边形 $A B C D$ 是矩形， $∠ A C P = 90 °$ ， $∠ A P C = ∠ P A D + ∠ P C D$ ．

(1)、求 $∠ A C D$ 的度数；

(2)、过点D作 $D E ⊥ A P$ ，垂足为点E，延长 $D E$ 交 $A C$ 于点F．请补全图形，探究线段 $A F$ ， $C F$ ， $P C$ 的数量关系，并证明．

查看试题解析
26. 定义：对于给定的两个函数，当 $x \geq 0$ 时，它们对应函数值相等；当 $x < 0$ 时，它们对应的函数值互为相反数．我们称这样的两个函数互为相关函数．
例如：一次函数 $y = - x + 2$ ，它的相关函数为 $y = {\begin{array}{l} - x + 2 (x \geq 0) \\ x - 2 (x < 0) \end{array}$

(1)、已知点 $M (- 1 ， m)$ 在一次函数 $y = - x + 2$ 的相关函数的图象上，则m的值为；

(2)、已知一次函数 $y = 2 x - 1$ ．
①这个函数的相关函数为；
②若点 $N (n ， 3)$ 在这个函数的相关函数的图象上，求n的值；
③当 $n \leq x \leq n + 1$ 时，这个函数的相关函数的取值范围是 $- 1 \leq y \leq 3$ ，直接写出n的取值范围．

查看试题解析