辽宁省鞍山市铁东区2020-2021学年八年级下学期期中数学试题
试卷更新日期：2022-03-10 类型：期中考试
一、单选题
-
1. 下列式子是最简二次根式的是（ ）A、 B、 C、 D、2. 以下列各组数为边长，能构成直角三角形的是（ ）A、7，12，13 B、1，1， C、2，3，4 D、 ， ，3. 如图，四边形ABCD是平行四边形，下列说法能判定四边形ABCD是菱形的是（ ）
A、AB＝CD B、BA⊥BD C、AC⊥BD D、AC＝BD4. 如图，已知正方形B的面积为144，正方形C的面积为169时，那么正方形A的面积为（ ）
A、313 B、144 C、169 D、255. 如图，在由边长均为1的小正方形组成的4×4网格中，将连接任意两个格点的线段称作“格点线”，则“格点线”的长度不可能为（ ）
A、5 B、 C、 D、6. 菱形ABCD的周长为40，它的一条对角线长10，则它的另一条对角线长为（ ）A、10 B、10 C、5 D、57. 如图，若AB//CD，AC交BD于点O，则下列条件中不能说明四边形ABCD是平行四边形的是（ ）
A、AD∥BC B、OA＝OC C、AD＝AB D、AB＝CD8. 如图，正方形中，点E是对角线上的一点，且 ， 连接 ， ， 则的度数为（ ）
A、20° B、22.5° C、25° D、30°二、填空题
-
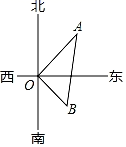
9. 已知平行四边形ABCD中，∠A+∠C=110°，则∠B的度数为 ．10. 如图，在水塔O的东北方向8m处有一抽水站A，在水塔的东南方向6m处有一建筑物工地B，在AB间建一条直水管，则水管的长为 ．
11. 一个正方形的对角线长为2，则其周长为 ．12. ．13. 小明学了在数轴上表示无理数的方法后，进行了练习：首先画数轴，原点为O，在数轴上找到表示数2的点A，然后过点A作AB⊥OA，使AB＝1；再以O为圆心，OB的长为半径作弧，交数轴正半轴于点P，那么点P表示的数是 ．
14. 如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形，如果大正方形的面积为16，直角三角形的面积为3，直角三角形的两直角边分别为a和b，那么（a+b）2的值为 ．
15. 如图，在四边形ABCD中，∠BAD＝∠ABC＝∠BCD＝∠ADC，AC与BD交于点O，且∠AOB＝60°，AB＝4，过B作BF⊥AC分别交AC、AD于E、F两点，过F作FG⊥BF交BD于G，则FG的长为 ．
16. 如图，在△ABC中，AC＝3，AB＝4，BC＝5，且△ABD，△ACF，△BCE都是等边三角形，下列结论中：①∠BAC＝90°；②四边形AFED为平行四边形；③四边形AFED面积为10；④∠DEF＝30°，正确的是 ． （填序号即可）
三、解答题
-
17. 计算： ．18. 如图，点E在矩形ABCD的边BC上，延长EB到点F，连接AF、DE，使AF＝DE．求证：BF＝CE．
19. 已知a＝2+ ， 求a2﹣4a﹣1的值．20. 如图，点D、E分别是△ABC的边AB、AC的中点，连接BE，过点C作CF∥BE，交DE的延长线于点F，若DE＝1，求DF的长．
21. 如图，已知△ABC、△BEF都是等腰直角三角形，且AB＝AC，BE＝EF，点A恰好在EF边上，若AE＝3，AC﹣BE＝1，求AF的长．
22. 如图，在正方形ABCD中，AB＝a，在其内部分别作正方形A1B1C1D1、A2B2C2D2、A3B3C3D3将正方形ABCD的面积四等分，且它们的顶点都在对角线AC、BD上，求A1B1、A2B2的长．（用含a的代数式表示）
23. 如图，在正方形ABCD中，点E、F、G分别AD、CD、AB边上三点，且BE⊥FG，过F作FH⊥AB交于H，连接BF、EF、GE；
(1)、求证：BE=FG；(2)、若△BEF为等边三角形，求证：GE=2AE．24. 如图，在ABC中，AB＝BC，∠ABC＞90°，E、D分别为线段AB、射线CB上两点，且AE＝DE，EFBC交AC于F，FGDE交直线BC于G．
(1)、求证：四边形DEFG为菱形；(2)、过F作FM⊥BC交于M，且GM＝3，FM＝4，N为EB中点，连接MN．①如图2，若点B与点G重合，求MN的长；
②当N恰好在四边形DEFG的边上时，请直接写出MN的长．