吉林省四平市铁西区2020-2021学年八年级下学期期中考试数学试题

试卷更新日期：2022-03-10 类型：期中考试

进入出卷网下载

一、单选题

1. 下列各式，计算正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $3 \sqrt{3} - \sqrt{3} = 3$ C、 $2 \sqrt{5} \times 3 \sqrt{5} = 6 \sqrt{5}$ D、 $(\sqrt{8} - \sqrt{6}) \div \sqrt{2} = 2 - \sqrt{3}$

查看试题解析
2. 若线段a，b，c组成直角三角形，则它们的比为（　　）

A、2∶3∶4 B、3∶4∶6 C、4∶6∶7 D、7∶24∶25

查看试题解析
3. 设 $\sqrt{2} = a ， \sqrt{10} = b$ ，用含a、b的式子表示 $\sqrt{20}$ ，下列表示正确的是 $($ 　　 $)$

A、2a B、2b C、a+b D、ab

查看试题解析
4. 下列判断不正确的是（）

A、对角线相等的四边形是矩形 B、对角线相互垂直平分的四边形是菱形 C、对角线相互垂直且相等的平行四边形是正方形 D、对角线相互平分的四边形是平行四边形

查看试题解析
5. 如图， $▱ A B C D$ 中，对角线 $A C$ 与 $B D$ 交于点O， $∠ D A C = 42 °$ ， $∠ C B D = 23 °$ ，则 $∠ C O D$ 是（）

A、63° B、65° C、67° D、69°

查看试题解析
6. 正方形ABCD的边AB上有一动点E，以EC为边作矩形ECFG，且边FG过点D，在点E从点A移动到点B的过程中，矩形ECFG的面积（）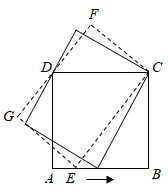

A、先变大后变小 B、先变小后变大 C、一直变大 D、保持不变

查看试题解析

二、填空题

7. 若二次根式 $\sqrt{2 x - 1}$ 有意义，则x的取值范围是．

查看试题解析
8. 已知直角三角形的两边长分别为3、4.则第三边长为.

查看试题解析
9. 已知n是一个正整数， $\sqrt{135 n}$ 是整数，则n的最小值是．

查看试题解析
10. 菱形的周长为20cm，一条对角线长为8cm，则菱形的面积为 cm².

查看试题解析
11. 如图，平移图形M，使其与图形N可以拼成一个平行四边形，则图中 $α$ 的度数是．

查看试题解析
12. 如图，在平行四边形 $A B C D$ 中，E、F分别是 $A B$ 、 $D C$ 上的点，请添加一个条件，使得四边形 $E B F D$ 为平行四边形，则添加的条件是．（答案不唯一，添加一个即可）．

查看试题解析
13. 如图，四边形 $A B C D$ 为菱形，四边形 $A O B E$ 为矩形， $O$ ， $C$ ， $D$ 三点的坐标为 $(0 ， 0)$ ， $(2 ， 0)$ ， $(0 ， 1)$ ，则点 $E$ 的坐标为.

查看试题解析
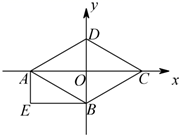14. 我国古代数学家赵爽的“勾股方圆图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形（如图所示），如果大正方形的面积是25，小正方形的面积是1，直角三角形的两直角边分别是a和b，那么 $a b$ 的值为．

查看试题解析

三、解答题

15. 计算： $\sqrt{12} + \sqrt{\frac{1}{3}} + \sqrt{{(\sqrt{3} - 2)}^{2}}$

查看试题解析
16. 计算： $\sqrt{18} + 4 \sqrt{\frac{1}{2}} - \sqrt{48} + \sqrt{\frac{1}{27}}$

查看试题解析
17. 已知实数a，b，c在数轴上所对应的点的位置如图所示，化简： $| a + b | - \sqrt{{(c - a)}^{2}} + \sqrt{c^{2}}$ ．

查看试题解析
18. 已知： $x = \sqrt{3} + 1 ， y = \sqrt{3} - 1$ ，求代数式 $x^{2} + 2 x y + y^{2}$ 的值.

查看试题解析
19. 求代数式 $a + \sqrt{a^{2} - 2 a + 1}$ 的值，其中 $a = - 2020$ ．如图是小亮和小芳的解答过程．

(1)、的解法是不正确的；

(2)、求代数式 $a + 2 \sqrt{a^{2} - 6 a + 9}$ 的值，其中 $a = - 2019$ ．

查看试题解析
20. 一艘轮船以30千米/时的速度离开港口，向东南方向航行，另一艘轮船同时离开港口，以40千米/时的速度航行，它们离开港口一个半小时后相距75千米，求第二艘船的航行方向．

查看试题解析
21. 利用矩形的性质，证明“直角三角形斜边上的中线等于斜边的一半”．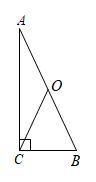
已知：如图，...............；
求证：...........；
证明：

查看试题解析
22. 如图， $A C / / D B$ ，且 $A C = 2 D B$ ， E是 $A C$ 的中点．

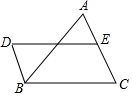(1)、求证：四边形 $B D E C$ 是平行四边形；

(2)、连接 $A D$ 、 $B E$ ，直接写出 $△ A B C$ 添加一个什么条件，使四边形 $D B E A$ 是矩形？（不用说明理由）

查看试题解析
23. 在进行二次根式计算时，我们有时会碰上如 $\frac{5}{\sqrt{3}} ， \sqrt{\frac{2}{3}} ， \frac{2}{\sqrt{3} + 1}$ 这样的式子，其实我们还可以将其进一步化简：
（一式） $\frac{5}{\sqrt{3}} = \frac{5 \times \sqrt{3}}{\sqrt{3} \times \sqrt{3}} = \frac{5}{3} \sqrt{3}$ ，
（二式） $\sqrt{\frac{2}{3}} = \sqrt{\frac{2 \times 3}{3 \times 3}} = \frac{\sqrt{6}}{3}$ ，
（三式） $\frac{2}{\sqrt{3} + 1} = \frac{2 \times (\sqrt{3} - 1)}{(\sqrt{3} + 1) (\sqrt{3} - 1)} = \frac{2 (\sqrt{3} - 1)}{{(\sqrt{3})}^{2} - 1^{2}} = \sqrt{3} - 1$ ．
以上这种化简的步骤叫做分母有理化．
（四式） $\frac{2}{\sqrt{3} + 1} = \frac{3 - 1}{\sqrt{3} + 1} = \frac{{(\sqrt{3})}^{2} - 1^{2}}{\sqrt{3} + 1} = \frac{(\sqrt{3} + 1) (\sqrt{3} - 1)}{\sqrt{3} + 1} = \sqrt{3} - 1$ ．

(1)、请用不同的方法化简 $\frac{2}{\sqrt{5} + \sqrt{3}}$
参照（三式）化简 $\frac{2}{\sqrt{5} + \sqrt{3}}$
参照（四式）化简 $\frac{2}{\sqrt{5} + \sqrt{3}}$

(2)、化简： $\frac{1}{\sqrt{3} + 1} + \frac{1}{\sqrt{5} + \sqrt{3}} + \frac{1}{\sqrt{7} + \sqrt{5}} + . . . + \frac{1}{\sqrt{2 n + 1} + \sqrt{2 n - 1}}$

查看试题解析
24. 如图，在四边形 $A B C D$ 中， $A B / / D C$ ， $A B = A D$ ，对角线 $A C$ 、 $B D$ 交于点O， $A C$ 平分 $∠ B A D$ ，过点C作 $C E ⊥ A B$ 交 $A B$ 的延长线于点E．

(1)、求证：四边形 $A B C D$ 是菱形；

(2)、若 $A B = 5$ ， $B D = 6$ ，求 $C E$ 的长．

查看试题解析
25. 如图，在Rt $△ A B C$ 中， $∠ C = 90 °$ ， $A B = 5 c m$ ， $A C = 4 c m$ ，动点P从点B出发沿射线 $B C$ 以 $3 c m / s$ 的速度移动，设运动的时间为 $t$ 秒．

(1)、求 $B C$ 边的长；

(2)、当 $△ A B P$ 为直角三角形时，求t的值；

(3)、当 $△ A B P$ 为等腰三角形时，请直接写出此时t的值．

查看试题解析
26. 如图所示，在正方形 $A B C D$ 中， $A B = 10$ ，点O为对角线交点， $B E = C F$ ，连接 $E F$ ，过点O作 $O G ⊥ E F$ 交 $B C$ 边于G，点G始终在 $B C$ 边上，并且不与点B、点C重合，连接 $O E$ 、 $O F$ 、 $E G$ ．

(1)、求证： $O E = O F$ ；

(2)、请求出 $∠ E O G$ 的度数？

(3)、试求出 $△ B E G$ 的周长；

(4)、若 $A E = A O$ ，请直接写出四边形 $B E O G$ 的面积．

查看试题解析