吉林省吉林市船营区2020-2021学年八年级下学期期中数学试题

试卷更新日期：2022-03-10 类型：期中考试

进入出卷网下载

一、单选题

1. 下列各式中是最简二次根式的是（）

A、 $\sqrt{\frac{5}{3}}$ B、 $\sqrt{12}$ C、 $\sqrt{15}$ D、 $\sqrt{18}$

查看试题解析
2. 下列四组线段中，可以构成直角三角形的是（）

A、2，3，4 B、4，5，6 C、7，8，9 D、1，1， $\sqrt{2}$

查看试题解析
3. 如图，在 $▱ A B C D$ 中．若 $∠ A = 12 0^{°}$ ，则 $∠ C$ 的度数为（）

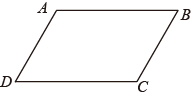A、60° B、120° C、70° D、110°

查看试题解析
4. 下列运算结果正确的是（）

A、 $\sqrt{10} - \sqrt{7} = \sqrt{3}$ B、 $2 + \sqrt{3} = 2 \sqrt{3}$ C、 $\sqrt{6} \div \sqrt{2} = 3$ D、 ${(\sqrt{2} - 1)}^{2} = 3 - 2 \sqrt{2}$

查看试题解析
5. 如图，以Rt△ABC的三边为直角边分别向外作等腰直角三角形．若AB= $\sqrt{5}$ ，则图中阴影部分的面积为（）

A、 $\frac{5}{2}$ B、 $\frac{25}{4}$ C、 $\frac{25}{2}$ D、5

查看试题解析
6. 如图，在正方形ABCD中，AB=6，点Q是AB边上的一个动点（点Q不与点B重合），点M，N分别是DQ，BQ的中点，则线段MN=（）

A、 $3 \sqrt{2}$ B、 $\frac{3 \sqrt{2}}{2}$ C、3 D、6

查看试题解析

二、填空题

7. 使二次根式 $\sqrt{2 x - 8}$ 有意义的x的取值范围是．

查看试题解析
8. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ， $A B = \sqrt{15}$ ， $A C = \sqrt{6}$ ，则 $B C$ 长是．

查看试题解析
9. 如图，在 $△ A B C$ 中，已知E、F、D分别是AB、AC、BC上的点，且 $D E / / A C$ ， $D F / / A B$ ，请你添加一个条件，使四边形AEDF是菱形．

查看试题解析
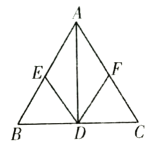10. 如图，OA＝OB，OC＝3，BC＝1，数轴上点A表示的数是.

查看试题解析
11. 如图，在 $▱ A B C D$ 中，已知 $A C = 4$ ，若 $△ A C D$ 的周长为13，则 $▱ A B C D$ 的周长为．

查看试题解析
12. 已知x、y为实数，且 $\sqrt{x - 1} + {(y - 2)}^{2} = 0$ ，则 $\sqrt{\frac{x}{y}}$ 的值为．

查看试题解析
13. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ， $A C = 4$ ，点D在BC上， $∠ A D C = 2 ∠ B$ ， $A D = 5$ ，则BC的长为．

查看试题解析
14. 如图，在矩形ABCD中，BD是对角线，延长AD到E，使DE＝BD，连接BE．若∠EBC＝27°，则∠ABD＝度．

查看试题解析

三、解答题

15. 计算： $4 \sqrt{20} - 3 \sqrt{45} + 2 \sqrt{5}$ ．

查看试题解析
16. 计算： $3 \sqrt{6} \times \frac{1}{3} \sqrt{30} \div \sqrt{2}$ ．

查看试题解析
17. 如图，在 $△ A B C$ 中， $A D ⊥ B C$ 于点D， $B D = 4$ ， $A D = 8$ ， $S_{△ A B C} = 76$ ，求AC的长．

查看试题解析
18. 如图，Rt△ABC中，∠C＝90°，M是AB的中点，AN＝ $\frac{1}{2}$ AB，AN $/ /$ CM．求证：MN＝AC．

查看试题解析
19. 已知 $x = 2 \sqrt{3} - 3 \sqrt{2}$ ， $y = 2 \sqrt{3} + 3 \sqrt{2}$ ，求 $x^{2} y + x y^{2}$ 的值．

查看试题解析
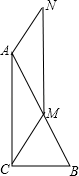20. 如图，正方形网格中的每个小正方形的边长都是1，每个小格的顶点叫格点，以格点为顶点分别按下列要求画图．

(1)、在图①中画一个面积为10的正方形；

(2)、在图②中画一个面积为12的菱形．

查看试题解析
21. 在《算法统宗》中有一道“荡秋千”的问题：“平地秋千未起，踏板一尺离地．送行二步与人齐，五尺人高曾记．仕女佳人争蹴，终朝笑语欢嬉．良工高士素好奇，算出索长有几”．此问题可理解为：如图，有一架秋千，当它静止时，踏板离地的距离AB的长度为1尺．将它往前推送，当水平距离为10尺时．即 $A^{'} C = 10$ 尺，则此时秋千的踏板离地的距离 $A^{'} D$ 就和身高5尺的人一样高．若运动过程中秋千的绳索始终拉得很直，求绳索OA的长．

查看试题解析
22. 如图，在 $△ A B C$ 中， $∠ B A C = 90 °$ ，点D是BC的中点， $A E / / B C$ ， $C E / / A D$ ．

(1)、求证：四边形ADCE是菱形；

(2)、过点D作 $D F ⊥ C E$ 于点F，若 $∠ B = 60 °$ ， $A B = 6$ ，则DF的长为．

查看试题解析
23. 如图，学校有一块三角形空地ABC，计划将这块三角形空地分割成四边形ABDE和△EDC，分别摆放“秋海棠”和“天竺葵”两种不同的花卉.经测量，∠EDC＝90°，DC＝6m，CE＝10 m，BD＝14 m，AB＝16m，AE＝2m.

(1)、求DE的长；

(2)、求四边形ABDE的面积.

查看试题解析
24. 如图，在平行四边形ABCD中， $A C ⊥ B C$ ，过点D作 $D E / / A C$ 交BC的延长线于点E，点M为AB的中点，连接CM．

(1)、求证：四边形ADEC是矩形；

(2)、若 $C M = 13$ ，且 $A C = 24$ ，求四边形ADEC的周长．

查看试题解析
25. 如图：

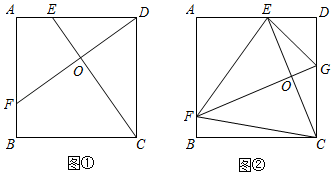(1)、基础探究：如图①，在正方形ABCD中，点E为AD上一点，DF⊥CE交AB于F，垂足为点O．求证：CE＝DF．

(2)、应用拓展：如图②，在正方形ABCD中，点E为AD上一点，FG⊥CE分别交AB、CD于F、G，垂足为点O．若正方形ABCD的边长为12，DE＝5，则四边形EFCG的面积为．

查看试题解析
26. 如图，在四边形ABCD中， $∠ B = 90 °$ ， $A D / / B C$ ， $A D = 16$ ， $B C = 21$ ， $C D = 13$ ．

(1)、求AB的长；

(2)、动点P从点B出发，沿射线BC以每秒2个单位长度的速度运动，同时动点Q从点A出发，沿线段AD以每秒1个单位长度的速度运动，当点Q运动到点D时，两点同时停止运动，设运动的时间为t秒．
①当t为何值时，以P、Q、D、C为顶点的四边形为平行四边形？
②是否存在点P，使 $△ P Q D$ 是以PQ为腰的等腰三角形？若存在，请直接写出相应的t的值；若不存在，请说明理由．

查看试题解析