黑龙江省双鸭山市集贤县2020-2021学年八年级下学期期中数学试题
试卷更新日期:2022-03-10 类型:期中考试
一、单选题
-
1. 下列二次根式中,属于最简二次根式的是( )A、 B、 C、 D、2. 二次根式有意义的条件是( )。
A、x>3 B、x>-3 C、x≥-3 D、x≥33. 如图,一个矩形纸片,剪去部分后得到一个三角形,则图中∠1+∠2的度数是( )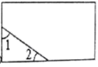 A、120° B、90 ° C、60° D、30°4. 矩形的两条对角线的夹角为60度,对角线长为15,则矩形的较短边长为( )A、12 B、10 C、7.5 D、55. 如图,以Rt△ABC的三边为边长向外作正方形,三个正方形的面积分别为 、 、 ,若 , ,则 的值为( )
A、120° B、90 ° C、60° D、30°4. 矩形的两条对角线的夹角为60度,对角线长为15,则矩形的较短边长为( )A、12 B、10 C、7.5 D、55. 如图,以Rt△ABC的三边为边长向外作正方形,三个正方形的面积分别为 、 、 ,若 , ,则 的值为( )
 A、1 B、5 C、25 D、1446. 能判定四边形是平行四边形的是( )A、对角线互相垂直 B、对角线相等 C、对角线互相垂直且相等 D、对角线互相平分7. 如图,在▱ABCD中,已知AD=5cm,AB=3cm,AE平分∠BAD交BC边于点E,则EC等于( )
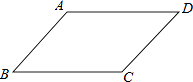
A、1 B、5 C、25 D、1446. 能判定四边形是平行四边形的是( )A、对角线互相垂直 B、对角线相等 C、对角线互相垂直且相等 D、对角线互相平分7. 如图,在▱ABCD中,已知AD=5cm,AB=3cm,AE平分∠BAD交BC边于点E,则EC等于( ) A、1cm B、2cm C、3cm D、4cm8. 如图,菱形ABCD中,E,F分别是AB,AC的中点,若EF=3,则菱形ABCD的周长是( )
A、1cm B、2cm C、3cm D、4cm8. 如图,菱形ABCD中,E,F分别是AB,AC的中点,若EF=3,则菱形ABCD的周长是( ) A、12 B、16 C、20 D、249. 如图,在矩形ABCD中,AB=8, , 将矩形沿AC折叠,点D落在点D'处,则重叠部分的面积为( )
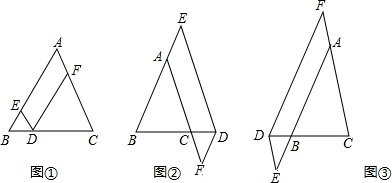
A、12 B、16 C、20 D、249. 如图,在矩形ABCD中,AB=8, , 将矩形沿AC折叠,点D落在点D'处,则重叠部分的面积为( ) A、6 B、8 C、10 D、1210. 如图,在中, , 是的中点,作 , 垂足在线段上,连接 , , 则下列结论:①;②;③;④ . 其中结论正确的序号是( )
A、6 B、8 C、10 D、1210. 如图,在中, , 是的中点,作 , 垂足在线段上,连接 , , 则下列结论:①;②;③;④ . 其中结论正确的序号是( )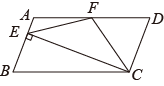 A、①② B、②③④ C、①②④ D、①②③④
A、①② B、②③④ C、①②④ D、①②③④二、填空题
-
11. 如图,在四边形ABCD中,AB∥CD,请你添加一个条件,使得四边形ABCD成为平行四边形,你添加的条件是 .
 12. 若 ,则x的取值范围是 .13. 在中, , 边上的高 , , 的长为 .14. 已知菱形的两条对角线长为8cm和6cm,那么这个菱形的周长是cm;15. .16. 如图,是的角平分线,交于 , 交于 . 且交于 , 则度.
12. 若 ,则x的取值范围是 .13. 在中, , 边上的高 , , 的长为 .14. 已知菱形的两条对角线长为8cm和6cm,那么这个菱形的周长是cm;15. .16. 如图,是的角平分线,交于 , 交于 . 且交于 , 则度.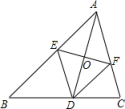 17. 如图,O是矩形ABCD的对角线AC的中点,M是AD的中点.若AB=5,AD=12,则四边形ABOM的周长为 .
17. 如图,O是矩形ABCD的对角线AC的中点,M是AD的中点.若AB=5,AD=12,则四边形ABOM的周长为 .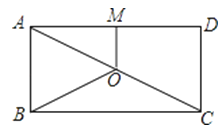 18. 如图,在△ABC 中,AC=BC,∠ACB=90°,点 D 在 BC 上,BD=3,DC=1,点 P 是 AB 上的动点,则 PC+PD 的最小值为
18. 如图,在△ABC 中,AC=BC,∠ACB=90°,点 D 在 BC 上,BD=3,DC=1,点 P 是 AB 上的动点,则 PC+PD 的最小值为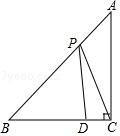 19. 观察下列各式: =2 ; =3 ; =4 ,……请你将发现的规律用含自然数n(n≥1)的等式表示出来 .
19. 观察下列各式: =2 ; =3 ; =4 ,……请你将发现的规律用含自然数n(n≥1)的等式表示出来 .三、解答题
-
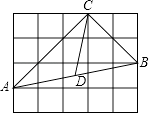
20. 如图,每个小正方形的边长为1,在△ABC中,点D为AB的中点,则线段CD的长为 .
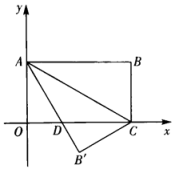
 21. 计算:(1)、(2)、22. 先化简在求值: ,其中23. 如图,已知CD=3,AD=4,BC=12,AB=13,∠ADC=90°,试求阴影部分的面积.
21. 计算:(1)、(2)、22. 先化简在求值: ,其中23. 如图,已知CD=3,AD=4,BC=12,AB=13,∠ADC=90°,试求阴影部分的面积.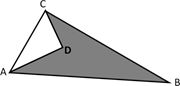 24. 正方形边长为 , , 分别是 , 边上的点, , 为的中点,连接 , , . 试判断的形状并说明理由.
24. 正方形边长为 , , 分别是 , 边上的点, , 为的中点,连接 , , . 试判断的形状并说明理由. 25. 如图,在▱ABCD 中,对角线 AC,BD 相交于点 O,过点 O 的一条直线分别交 AD,BC 于点 E,F.求证:AE=CF.
25. 如图,在▱ABCD 中,对角线 AC,BD 相交于点 O,过点 O 的一条直线分别交 AD,BC 于点 E,F.求证:AE=CF.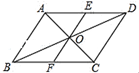 26. 如图,顺次链接矩形各边中点,得到四边形 , 求证:四边形是菱形.
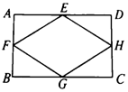
26. 如图,顺次链接矩形各边中点,得到四边形 , 求证:四边形是菱形.