广东省中山市2020-2021学年八年级下学期期中数学试题

试卷更新日期：2022-03-10 类型：期中考试

进入出卷网下载

一、单选题

1. 若式子 $\sqrt{2 x - 2}$ 在实数范围内有意义，则x的取值范围是（）

A、x≠1 B、x≥1 C、x≤1 D、x≠﹣1

查看试题解析
2. 下列各组数据中，不能作为直角三角形的三边长的是（）

A、3，4，5 B、9，12，15 C、1， $\sqrt{3}$ ， 2 D、5，12，14

查看试题解析
3. 下列等式成立的是（）

A、3+ $\sqrt{3}$ ＝3 $\sqrt{3}$ B、 $\sqrt{8}$ ﹣ $\sqrt{3}$ ＝ $\sqrt{5}$ C、3×3 $\sqrt{2}$ ＝3 $\sqrt{6}$ D、 $\sqrt{(- 4)^{2}}$ ＝4

查看试题解析
4. 下列命题中，逆命题是真命题的是（）

A、平行四边形的两组对角分别相等 B、全等三角形的对应角相等 C、对顶角相等 D、如果a＞b，b＞0，那么a+b＞0

查看试题解析
5. 下列根式中属最简二次根式的是（）

A、 $\sqrt{\frac{1}{3}}$ B、 $\sqrt{a^{2} - 1}$ C、 $\sqrt{8}$ D、 $\frac{1}{\sqrt{2}}$

查看试题解析
6. 对角线互相垂直平分且相等的四边形一定是（）

A、正方形 B、菱形 C、矩形 D、平行四边形

查看试题解析
7. 等腰三角形的腰长为13，底长为10，则这个等腰三角形底边上的高是（）

A、10 B、12 C、8 D、11

查看试题解析
8. 如图，平行四边形ABCD的对角线AC的垂直平分线交AD于点E，连接CE．若平行四边形ABCD的周长为24cm，则△CDE的周长为（）

A、12cm B、24cm C、15cm D、18cm

查看试题解析
9. 如图，菱形ABCD的两条对角线AC，BD相交于点O，E是AB的中点，若AC=6，菱形ABCD的面积为24，则OE长为（）

A、3.5 B、3 C、2.5 D、2

查看试题解析
10. 把一张矩形纸片ABCD按如图方式折叠，使顶点B和点D重合，折痕为EF．若AB=4，BC=8．则△DEF的面积是（）

A、6 B、10 C、12 D、4

查看试题解析

二、填空题

11. 化简： $\frac{\sqrt{18} - \sqrt{8}}{\sqrt{2}}$ ＝．

查看试题解析
12. 如图，在数轴上找到表示-3的点B，过点A作AB⊥OB，AB=2，以O为圆心，OA为半径作弧，弧与数轴交于点C，则点C在数轴上表示的数是．

查看试题解析
13. 计算 $5 \div \sqrt{5} \times \frac{1}{\sqrt{5}}$ 所得的结果是．

查看试题解析
14. 如图，在△ABC中，AD⊥BC于点D，∠B=60°，∠C=45°，BD=2 ，则AC= ．

查看试题解析
15. 如图，平面内直线 $l_{1} / / l_{2} / / l_{3} / / l_{4}$ ，且相邻两条平行线间隔均为1，正方形 $A B C D$ 四个顶点分别在四条平行线上，则正方形的面积为．

查看试题解析
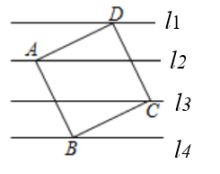16. 在矩形ABCD中，对角线AC ， BD交于点O ， DE平分∠ADC ，交BC于点E ， ∠BDE=15°，则∠COD= ．

查看试题解析
17. 如图，△ABC的周长为16，连接△ABC三边中点构成第一个△A₁B₁C₁ ，再连接△A₁B₁C₁的三边中点构成第二个△A₂B₂C₂ ，依此类推，则第2021个三角形的周长为．

查看试题解析

三、解答题

18. 计算： $\sqrt{27} - 6 \sqrt{\frac{1}{2}} + \sqrt{6} (\sqrt{8} + \sqrt{3})$ ．

查看试题解析
19. 如图，在离水面高度为8米的岸上，有人用绳子拉船靠岸，开始时绳子 $B C$ 的长为17米，此人以1米每秒的速度收绳，7秒后船移动到点 $D$ 的位置，问船向岸边移动了多少米？（假设绳子是直的）

查看试题解析
20. 如图在平行四边形ABCD的对角线AC的延长线上取两点E、F，使EA＝CF，求证：四边形EBFD是平行四边形.

查看试题解析
21. 已知x=2+ $\sqrt{3}$ ， y=2- $\sqrt{3}$ ，求下列各式的值：

(1)、x²+y²+3xy；

(2)、 $\frac{1}{x} + \frac{1}{y}$ ．

查看试题解析
22. 如图，在△ABC中，∠C=90°，AC=8，BC=6，DE是△ABD的边AB上的高，且AD=2 $\sqrt{5}$ ， BD＝4 $\sqrt{5}$ ．求DE的长．

查看试题解析
23. 如图，在△ABC中，∠BAC＝90°，AD是BC边上的中线，E是AD的中点，过点A作BC的平行线与BE的延长线相交于点F，连接CF．

(1)、求证：四边形CFAD是菱形；

(2)、若AB＝4，BD＝ $\frac{5}{2}$ ，求四边形CFAD的面积．

查看试题解析
24. 如图，平行四边形ABCD中，AB=4cm，BC=6cm，∠B=60°，G是CD的中点，E是边AD上的动点，EG的延长线与BC的延长线交于点F，连接CE，DF．

(1)、求证：四边形CEDF是平行四边形；

(2)、请直接写出当AE为何值时，四边形CEDF是菱形（不用证明）．

(3)、当AE＝4时，请证明：四边形CEDF是矩形．

查看试题解析
25. 如图1，在四边形ABCD中，AD∥BC，AD＝acm，BC＝bcm，b满足 $b = \sqrt{a - 6} + \sqrt{6 - a} + 8$ ，若动点P从A点出发，以每秒0.5cm的速度沿线段AD向点D运动；点Q从C点出发以每秒2cm的速度沿CB方向运动，动点P、Q同时停止运动，回答下列问题：

(1)、AD＝cm，BC＝cm．

(2)、设点P、Q同时出发，并运动了x秒，求当x为多少秒时，四边形PQCD成为平行四边形？

(3)、如图2，若四边形ABCD变为平行四边形ABCD，AD＝BC＝6cm，以每秒0.5cm的速度沿线段AD向点D运动；动点Q从C点出发以每秒2cm的速度在BC间往返运动，P，Q两点同时出发，当点P到达点D时停止运动（同时Q点也停止），求当t为多少秒时，以P，D，Q，B四点组成的四边形是平行四边形．

查看试题解析