广东省阳江市阳东区2020-2021学年八年级下学期期中数学试题

试卷更新日期：2022-03-10 类型：期中考试

进入出卷网下载

一、单选题

1. 要使二次根式 $\sqrt{x - 3}$ 有意义，则x的取值可以是（）

A、0 B、1 C、2 D、4

查看试题解析
2. 下列计算中，正确的是（）

A、 $\sqrt{3} + \sqrt{4} = \sqrt{7}$ B、 $2 + \sqrt{2} = 2 \sqrt{2}$ C、 $\sqrt{3} \times \sqrt{5} = \sqrt{15}$ D、 $2 \sqrt{3} - 2 = \sqrt{3}$

查看试题解析
3. 在Rt△ABC中，∠B＝90°，∠C＝30°，AC＝2．则BC的长为（）

A、1 B、2 C、 $\sqrt{3}$ D、 $\sqrt{5}$

查看试题解析
4. 如图，学校有一块长方形花铺，有极少数人为了避开拐角走“捷径”，在花铺内走出了一条“路”．他们仅仅少走了（）步路（假设2步为1米），却踩伤了花草．

A、1 B、2 C、3 D、4

查看试题解析
5. 下列计算正确的是（）

A、 $\sqrt{{(- 1)}^{2}} = \pm 1$ B、 $\sqrt{27} \div \sqrt{3} = 9$ C、 $\frac{\sqrt{8} \times \sqrt{6}}{\sqrt{2}} = \sqrt{4} \times \sqrt{3}$ D、 $\frac{1}{\sqrt{2} - 1} = \sqrt{2} + 1$

查看试题解析
6. 如图，有两颗树，一颗高10米，另一颗高4米，两树相距8米．一只鸟从一颗树的树梢飞到另一颗树的树梢，问小鸟至少飞行（）

A、8米 B、10米 C、12米 D、14米

查看试题解析
7. 已知菱形的边长为 $3$ ，较短的一条对角线的长为 $2$ ，则该菱形较长的一条对角线的长为（）

A、 $2 \sqrt{2}$ B、 $2 \sqrt{5}$ C、 $4 \sqrt{2}$ D、 $2 \sqrt{10}$

查看试题解析
8. E为矩形ABCD的边CD上的一点，AB=AE=4，BC=2，则∠BEC是（）．

A、15° B、30° C、60° D、75°

查看试题解析
9. 如图，在平面直角坐标系中，菱形ABCD的顶点A，B的坐标分别是（0，0），（2，0），∠α＝60°，则顶点C在第一象限的坐标是（）

A、（2，2） B、（3， $\sqrt{3}$ ） C、（3，2） D、（ $\sqrt{3}$ +1， $\sqrt{3}$ ）

查看试题解析
10. 我国古代数学家赵爽“的勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形（如图所示），如果大正方形的面积是25，小正方形的面积是1，直角三角形的两直角边分别是a、b，那么 ${(a + b)}^{2}$ 的值为（）.

A、49 B、25 C、13 D、1

查看试题解析

二、填空题

11. 比较大小： $2 \sqrt{3}$ $3 \sqrt{2}$ （填“＞”、“＜”或“＝”）.

查看试题解析
12. 计算： $5 \sqrt{2} - 2 \sqrt{2}$ ．

查看试题解析
13. 如图所示，在 $R t Δ A B C$ 中， $∠ A C B = 90 °$ ， $C M$ 是斜边 $A B$ 上的中线， $E 、 F$ 分别为 $M B 、 B C$ 的中点，若 $E F = 1$ ，则 $A B =$ ．

查看试题解析
14.
如图，在平面直角坐标系中，点A，B的坐标分别为（﹣6，0）、（0，8）．以点A为圆心，以AB长为半径画弧，交x正半轴于点C，则点C的坐标为

查看试题解析
15. 如图，在Rt△ABC中，∠B＝90°，AB＝8，BC＝6，AC的垂直平分线DE分别交AB，AC于D，E两点，则CD的长为．

查看试题解析
16. 实数 $a$ 、 $b$ 在数轴上的位置，化简 $\sqrt{a^{2}} - \sqrt{b^{2}} - \sqrt{{(a - b)}^{2}} =$ .

查看试题解析
17. 如图，在矩形ABCD中，AD=6，对角线AC，BD相交于O，AE⊥BD于E，且AE平分∠BAC，则AB的长为

查看试题解析

三、解答题

18. 计算：（﹣3）⁰+ $\sqrt{8}$ +（﹣3）²﹣2× $\frac{\sqrt{2}}{2}$ ．

查看试题解析
19. 如图， $▱ A B C D$ 中，点E是边AD的中点，连接CE并延长交BA的延长线于点F，连接AC，DF．求证：四边形ACDF是平行四边形．

查看试题解析
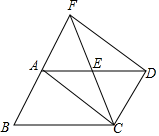20. 如图，小方格都是边长为1的正方形．你能判断△ABC的形状吗？试试吧！

查看试题解析
21. 图①，图②均为正方形网格，每个小正方形的边长均为l，各个小正方形的顶点叫做格点，请在下面的网格中按要求分别画图，使得每个图形的顶点均在格点上．

(1)、画一个直角三角形，且三边长为 $\sqrt{5}$ ， 2 $\sqrt{5}$ ， 5；

(2)、画一个边长为整数的等腰三角形，且面积等于12．

查看试题解析
22. 已知 $a = \frac{2}{\sqrt{2}}$ ， $b 、 c$ 满足 $\sqrt{b - 3} + | c - \sqrt{11} | = 0$ .

(1)、求 $b 、 c$ 的值；

(2)、试问以 $a 、 b 、 c$ 为边能否构成三角形？若能，求出三角形的面积；若不能，说明理由.

查看试题解析
23. 在正方形ABCD中，对角线BD所在的直线上有两点E、F满足BE=DF，连接AE、AF、CE、CF，如图所示．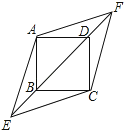

(1)、求证：△ABE≌△ADF；

(2)、试判断四边形AECF的形状，并说明理由．

查看试题解析
24. 如图，四边形ACFD是一个边长为b的正方形，延长FC到B，使BC＝a，连接AB，使AB＝C；E是边DF上的点且DE＝a．

(1)、判断△ABE的形状，并证明你的结论；

(2)、用含b的式子表示四边形ABFE的面积；

(3)、求证：a²+b²＝c² ．

查看试题解析
25. 如图，在矩形ABCD中，AB＝3cm，BC＝6cm.点P从点D出发向点A运动，运动到点A即停止；同时，点Q从点B出发向点C运动，运动到点C即停止，点P、Q的速度都是1cm/s.连接PQ、AQ、CP.设点P、Q运动的时间为ts.

(1)、当t为何值时，四边形ABQP是矩形，请说明理由；

(2)、当t为何值时，四边形AQCP是菱形，请说明理由；

(3)、直接写出（2）中菱形AQCP的周长和面积，周长是cm，面积是cm².

查看试题解析