广东省深圳市福田区三部联考2020-2021学年八年级下学期期中数学试题

试卷更新日期：2022-03-10 类型：期中考试

进入出卷网下载

一、单选题

1. 保护环境，人人有责．下列四个图形是生活中常见的垃圾回收标志，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 已知x＜y，则下列结论不成立的是（）

A、x﹣2＜y﹣2 B、 $\frac{x}{2} < \frac{y}{2}$ C、3x+1＜3y+1 D、﹣2x＜﹣2y

查看试题解析
3. 若分式 $\frac{x}{3 - x}$ 有意义，则 $x$ 的取值范围是（）

A、 $x \leq 3$ B、 $x < 3$ C、 $x < 3$ 且 $x \neq 0$ D、 $x \neq 3$

查看试题解析
4. 下列等式从左到右的变形是因式分解的是（）

A、2x（x+3）＝2x²+6x B、x²﹣y²＝（x+y）（x﹣y） C、x²+2xy+y²+1＝（x+y）²+1 D、24xy²＝3x•8y²

查看试题解析
5. 在平面直角坐标系中，已知点A（1，3），将点A向左平移3个单位后，再将它向上平移4个单位，则它的坐标变为（）

A、（﹣2，7） B、（4，﹣1） C、（4，7） D、（﹣2，﹣1）

查看试题解析
6. 下列说法正确的是（）

A、一组对边平行，另一组对边相等的四边形是平行四边形 B、对角线相等的平行四边形是菱形 C、三个角都是直角的四边形是矩形 D、正八边形的每一个外角都等于40°

查看试题解析
7. 直线 $l_{1} ： y = k_{1} x + b$ 与直线 $l_{2} ： y = k_{2} x$ 在同一平面直角坐标系中的图象如图所示，则关于x的不等式 $k_{2} x > k_{1} x + b$ 的解集为（）

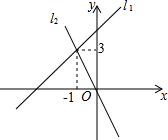A、x＞3 B、x＜3 C、x＞﹣1 D、x＜﹣1

查看试题解析
8. 某口罩生产企业最近要紧急完成1000万只口罩生产的任务，在生产完400万只口罩后，新的生产线安装完毕，可以加入生产了；新的生产线加入后，每天口罩的生产总量比原来增加了 $50 %$ ，结果共用了8天完成了任务设新生产线加入前，每天生产口罩 $x$ 万只，则根据题意可得方程为（）

A、 $\frac{400}{x} + \frac{1000}{(1 + 50 %) x} = 8$ B、 $\frac{400}{x} + \frac{1000 - 400}{(1 + 50 %) x} = 8$ C、 $\frac{400}{x} + \frac{1000 - 400}{50 % x} = 8$ D、 $\frac{1000}{x} + \frac{1000 - 400}{(1 + 50 %)) x} = 8$

查看试题解析
9. 如图，菱形ABCD的对角线AC、BD相交于点O ，过点C作CE⊥AD于点E ，连接OE ，若OB＝8，S_菱形_ABCD＝96，则OE的长为（）

A、2 $\sqrt{3}$ B、2 $\sqrt{5}$ C、6 D、8

查看试题解析
10. 等边三角形ABC的边长为6，点O是三边垂直平分线的交点，∠FOG＝120°，∠FOG的两边OF，OG与AB，BC分别相交于D，E，∠FOG绕O点顺时针旋转时，下列四个结论：①OD＝OE；②S_△ODE＝S_△BDE；③S_四_边_形ODBE＝ $\frac{27}{8} \sqrt{3}$ ；④△BDE周长最小值是9．其中正确个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 因式分解： $m x^{2} - 4 m x y + 4 m y^{2} =$ ．

查看试题解析
12. 如图，CE是∠ACD的平分线，CD∥AB，DE⊥CE，若∠DEB=32°，则∠A的度数为．

查看试题解析
13. 若关于 $x$ 的分式方程 $\frac{x + m}{x - 2} + \frac{3 m}{2 - x} = 2$ 有增根，则 $m$ 的值为.

查看试题解析
14. 已知平行四边形ABCD三个顶点的坐标分别为A（﹣1，0），B（5，0），C（7，4）．直线y＝kx+1将平行四边形ABCD分成面积相等的两部分，则k的值为．

查看试题解析
15. 如图，已知D（6，0），MN∥x轴且经过点E（0，4），点A，B分别是线段OD，OE上的两动点，AB=2，点C为AB的中点，点P为直线MN在第一象限上的动点，连接PC、PD，则PC+PD的最小值为．

查看试题解析

三、解答题

16. 解不等式组 ${\begin{array}{l} 3 (x - 2) \leq x - 4 \\ \frac{1 + 2 x}{3} > x - 1 \end{array}$ ，并将其解集在下面的数轴上表示出来．

查看试题解析
17. 解分式方程： $\frac{1 - x}{x - 2} = \frac{1}{2 - x} - 2$

查看试题解析
18. 先化简，再求值：（a﹣1﹣ $\frac{3}{a + 1}$ ）÷ $\frac{a^{2} - 4 a + 4}{a + 1}$ ，请在﹣ $\sqrt{2}$ ~ $\sqrt{5}$ 范围内选择一个合适的整数代入求值．

查看试题解析
19. 如图，在平面直角坐标系中，已知△ABC的三个顶点坐标分别是A（5，4），B（1，1），C（5，1）．
⑴请画出△ABC关于x轴对称的△A₁B₁C₁ ，并写出点A₁的坐标；
⑵以O为对称中心，画出△ABC关于O成中心对称的图形△A'B'C'；
⑶请用无刻度的直尺画出∠ABC的平分线BQ（点Q在线段AC上）（保留作图辅助线）．

查看试题解析
20. 某商店五月份销售A型电脑的总利润为4320元，销售B型电脑的总利润为3060元，且销售A型电脑数量是销售B型电脑的2倍，已知销售一台B型电脑比销售一台A型电脑多获利50元．

(1)、求每台A型电脑和B型电脑的利润；

(2)、该商店计划一次购进两种型号的电脑共100台且全部售出，其中B型电脑的进货量不超过A型电脑的2倍，该商店购进A型、B型电脑各多少台，才能使销售总利润最大？最大利润是多少？

查看试题解析
21. 如图，在菱形ABCD中，对角线AC，BD交于点O，过点A作AE⊥BC于点E，延长BC到点F，使得CF=BE，连接DF，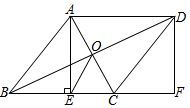

(1)、求证：四边形AEFD是矩形；

(2)、连接OE，若AB＝13，OE＝2 $\sqrt{13}$ ，求AE的长．

查看试题解析
22. 已知：直线y＝ $\frac{3}{4} x$ +6与x轴、y轴分别相交于点A和点B，点C在线段AO上．将△ABO沿BC折叠后，点O恰好落在AB边上点D处．

(1)、直接写出A、B两点的坐标：A：， B：；

(2)、求出OC的长；

(3)、如图，点E、F是直线BC上的两点，若△AEF是以EF为斜边的等腰直角三角形，求点F的坐标；

(4)、取AB的中点M，若点P在y轴上，点Q在直线AB上，是否存在以C、M、P、Q为顶点的四边形为平行四边形？若存在，请求出所有满足条件的Q点坐标；若不存在，请说明理由．

查看试题解析