广东省茂名市化州市2020-2021学年八年级下学期期中数学试题

试卷更新日期：2022-03-10 类型：期中考试

进入出卷网下载

一、单选题

1. 已知x＜y，则下列结论不成立的是（）

A、x﹣2＜y﹣2 B、 $\frac{x}{2} < \frac{y}{2}$ C、3x+1＜3y+1 D、﹣2x＜﹣2y

查看试题解析
2. 在平面直角坐标系内，将点A（1，2）先向右平移2个单位长度，再向下平移1个单位长度，则平移后所得点的坐标是（　　）

A、（3，1） B、（3，3） C、（﹣1，1） D、（﹣1，3）

查看试题解析
3. 下列四个圆形图案中，既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 不等式组 ${\begin{array}{l} 2 - x \geq 0 \\ 3 x + 2 > - 1 \end{array}$ 的解集是（）

A、﹣1＜x≤2 B、﹣2≤x＜1 C、x＜﹣1或x≥2 D、2≤x＜﹣1

查看试题解析
5. 已知等腰三角形有一边长为 $5$ ，一边长为 $2$ ，则其周长为（）

A、 $12$ B、 $9$ C、 $10$ D、12或9

查看试题解析
6. 如图所示，在等边三角形ABC中，AD⊥BC，E为AD上一点，∠CED＝50°，则∠ABE等于（）

A、10° B、15° C、20° D、25°

查看试题解析
7. 如图，在Rt△ABC中，∠BAC＝90°，将△ABC绕点A顺时针旋转90°后得到△AB'C'（点B对应点是点B'，点C'的对应点是点C'），连接CC'．若∠CC'B'＝22°，则∠B的大小是（）

A、63° B、67° C、68° D、77°

查看试题解析
8. 如图，在 $△ A B C$ 中， $∠ A = 87 ° ， ∠ A B C$ 的平分线 $B D$ 交 $A C$ 于点 $D ， E$ 是 $B C$ 中点，且 $D E ⊥ B C$ ，那么 $∠ C$ 的度数为（）

A、 $16 °$ B、 $28 °$ C、 $31 °$ D、 $62 °$

查看试题解析
9. 如图，AD是△ABC中∠BAC的角平分线，DE⊥AB于点E，S_△_ABC=9，DE=2，AB=5，则AC长是（）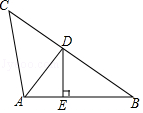

A、3 B、4 C、5 D、6

查看试题解析
10. 一次函数 $y_{1} = a x + b$ 与 $y_{2} = c x + d$ 的图象如图所示，下列说法：① $a b ＜ 0$ ；②函数 $y = a x + d$ 不经过第一象限；③不等式 $a x + b ＞ c x + d$ 的解集是 $x ＜ 3$ ；④ $a - c = \frac{1}{3} (d - b)$ ．其中正确的个数有（）

A、4 B、3 C、2 D、1

查看试题解析

二、填空题

11. 不等式x+3＞5的解集为．

查看试题解析
12.
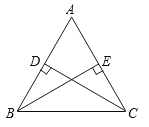
如图，BE，CD是△ABC的高，且BD＝EC，判定△BCD≌△CBE的依据是“”．

查看试题解析
13. 已知一次函数y＝mx+3（m≠0）的图象经过点（3，0），则关于x的不等式mx+3＞0的解集是．

查看试题解析
14. 在平面直角坐标系中，将点（﹣2，5）向左平移4个单位长度后得到的点的坐标为．

查看试题解析
15. 如图，将△ABC绕点A顺时针旋转得到△ADE，且点D恰好在AC上，∠BAE＝∠CDE＝136°，则∠C的度数是．

查看试题解析
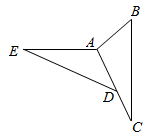16. 不等式组 ${\begin{array}{l} 4 x - 6 \leq x + 3 \\ 7 + x < 6 + 2 x \end{array}$ 的所有整数解的和是．

查看试题解析
17. 如图，Rt△ABC中，∠ABC＝90°，DE是边AB的垂直平分线，D为垂足，DE交AC于点E，且AB＝8，BC＝6，则△BEC的周长是.

查看试题解析

三、解答题

18. 解不等式 $\frac{10 - x}{3} \leq 2 x + 1$ ．

查看试题解析
19. 解不等式组 ${\begin{array}{l} 3 x < x + 2 ， ① \\ \frac{x + 1}{2} \geq \frac{2 x + 1}{5} . ② \end{array}$ 并把解集在数轴上表示出来．

查看试题解析
20. 如图，在△ABC中，AB＝AC，∠A＝36°，BD平分∠ABC交AC于点D，点E是AB的中点，连接DE．求证：△ABD是等腰三角形．

查看试题解析
21. 如图，在正方形网格中建立平面直角坐标系，已知点A（0，﹣2），B（2，﹣5），C（5，﹣3），请按下列要求操作：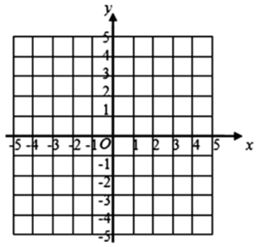
⑴请在图中画出△ABC；
⑵将△ABC向上平移5个单位长度，再向左平移4个单位长度，得到△A₁B₁C₁.在图中画出△ABC，并直接写出点A₁、B₁、C₁的坐标．

查看试题解析
22. 若关于x、y的二元一次方程组 ${\begin{cases} 2 x + y = - 3 m + 2 \\ x + 2 y = 4 \end{cases}$ 的解满足x+y＞﹣ $\frac{3}{2}$ ，求出满足条件的m的所有正整数值.

查看试题解析
23. 在Rt△ABC中，∠ACB＝90°，∠B＝30°，将△ABC绕点C顺时针旋转一定角度得到△DEC，点D恰好在AB上．

(1)、若AC＝4，求DE的值；

(2)、确定△ACD的形状，并说明理由．

查看试题解析
24. 如图，△ABC中，AB＝AC，AB的垂直平分线DE分别交AC、AB点D、E．

(1)、若∠A＝50°，求∠CBD的度数；

(2)、若AB＝7，△CBD周长为12，求BC的长．

查看试题解析
25. 如图，在△ABC中，∠ACB＝90°，∠B＝30°，CE垂直于AB于点E，D是AB的中点．

(1)、求证：AE＝ED；

(2)、若AC＝2，求DE的长．

查看试题解析