广东省揭阳市普宁市2020-2021学年八年级下学期期中数学试题
试卷更新日期:2022-03-10 类型:期中考试
一、单选题
-
1. 下面的图形是用数学家名字命名的,其中既是轴对称图形又是中心对称图形的是( )A、
 赵爽弦图
B、
赵爽弦图
B、 笛卡尔心形线
C、
笛卡尔心形线
C、 科克曲线
D、
科克曲线
D、 斐波那契螺旋线
2. 若 , 则下列式子中不正确的是( )A、 B、 C、 D、3. 用反证法证明命题:“已知△ABC,AB=AC,求证:∠B<90°.”第一步应先假设( )A、∠B≥90° B、∠B>90° C、∠B<90° D、AB≠AC4. 不等式的解集为( )A、 B、 C、 D、5. 如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=2,则AB等于( )
斐波那契螺旋线
2. 若 , 则下列式子中不正确的是( )A、 B、 C、 D、3. 用反证法证明命题:“已知△ABC,AB=AC,求证:∠B<90°.”第一步应先假设( )A、∠B≥90° B、∠B>90° C、∠B<90° D、AB≠AC4. 不等式的解集为( )A、 B、 C、 D、5. 如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=2,则AB等于( )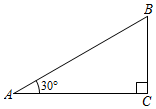 A、2 B、3 C、4 D、66. 不等式组 的解集在数轴上表示正确的是( )A、
A、2 B、3 C、4 D、66. 不等式组 的解集在数轴上表示正确的是( )A、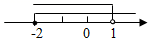 B、
B、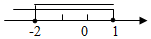 C、
C、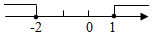 D、
D、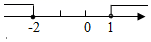 7. 在△ABC中, ∠A的相邻外角是70°,要使△ABC为等腰三角形, 则∠B为 ( )A、70° B、35° C、110° 或 35° D、110°8. 如图,直线经过点(2,0),则关于的不等式的解集是( )
7. 在△ABC中, ∠A的相邻外角是70°,要使△ABC为等腰三角形, 则∠B为 ( )A、70° B、35° C、110° 或 35° D、110°8. 如图,直线经过点(2,0),则关于的不等式的解集是( ) A、 B、 C、 D、9. 如图,在△ABC中,∠C=90°,按以下步骤作图:①以点A为圆心、适当长为半径作圆弧,分别交边AC,AB于点M、N;②分别以点M和点N为圆心、大于 MN的长为半径作圆弧,在∠BAC内,两弧交于点P;③作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是( )
A、 B、 C、 D、9. 如图,在△ABC中,∠C=90°,按以下步骤作图:①以点A为圆心、适当长为半径作圆弧,分别交边AC,AB于点M、N;②分别以点M和点N为圆心、大于 MN的长为半径作圆弧,在∠BAC内,两弧交于点P;③作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是( )
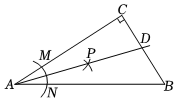
A、15 B、30 C、45 D、6010. 如图,将折线记作 , 其中 , , , 依次将沿轴正方向平移4个单位得 , 再将向右平移4个单位得…,若点在上,则的值是( )
A、15 B、30 C、45 D、6010. 如图,将折线记作 , 其中 , , , 依次将沿轴正方向平移4个单位得 , 再将向右平移4个单位得…,若点在上,则的值是( ) A、0 B、 C、 D、
A、0 B、 C、 D、二、填空题
-
11. 命题:“全等三角形的周长相等”的逆命题是;该逆命题是命题.(填“真”或“假”)12. 如图,△ABC中,AD⊥BC于D,要使△ABD≌△ACD,若根据“HL”判定,还需要加条件 .
 13. 如图,将 绕点 按逆时针方向旋转45°后得到 ,若 ,则 度.
13. 如图,将 绕点 按逆时针方向旋转45°后得到 ,若 ,则 度. 14. 若点 , 将点向右平移2个单位长度后落在轴上,则 .15. 如图,在 中,AB的垂直平分线交A于点D , 交BC于点E , 若 , ,则 的周长为 .
14. 若点 , 将点向右平移2个单位长度后落在轴上,则 .15. 如图,在 中,AB的垂直平分线交A于点D , 交BC于点E , 若 , ,则 的周长为 . 16. 某电器商场促销,海尔某型号冰箱的售价是2500元,进价是1800元,商场为保证利润率不低于5%,则海尔该型号冰箱最多降价元.17. 如图,中, , , , 是线段上一个动点,以为边在外作等边 . 若是的中点,则的最小值为 .
16. 某电器商场促销,海尔某型号冰箱的售价是2500元,进价是1800元,商场为保证利润率不低于5%,则海尔该型号冰箱最多降价元.17. 如图,中, , , , 是线段上一个动点,以为边在外作等边 . 若是的中点,则的最小值为 .
三、解答题
-
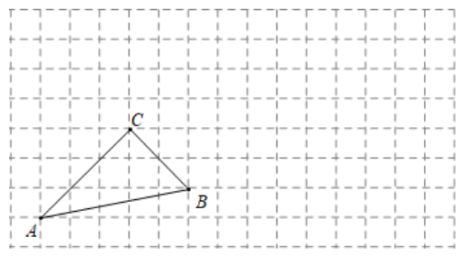
18. 已知代数式的值不小于代数式的值,试确定的最小整数值.19. 在方形网格图中,把向右平移5个方格,得到 , 再绕点顺时针方向旋转 , 得到 , 画出平移和旋转后的图形,并标明对应字母.
 20. 解不等式组 ,并在数轴上表示其解集.21. 如图,已知等腰三角形ABC的顶角∠A=108°.
20. 解不等式组 ,并在数轴上表示其解集.21. 如图,已知等腰三角形ABC的顶角∠A=108°. (1)、在BC上作一点D,使AD=CD(要求:尺规作图,保留作图痕迹,不必写作法和证明).(2)、求证:△ABD是等腰三角形.22. 如图所示, , 分别表示使用一种白炽灯和一种节能灯的费用 (费用=灯的售价+电费,单位:元)与照明时间 (小时)的函数图象,其中: 的函数解析式为 . 假设两种灯的使用寿命都是2000小时,照明效果一样.
(1)、在BC上作一点D,使AD=CD(要求:尺规作图,保留作图痕迹,不必写作法和证明).(2)、求证:△ABD是等腰三角形.22. 如图所示, , 分别表示使用一种白炽灯和一种节能灯的费用 (费用=灯的售价+电费,单位:元)与照明时间 (小时)的函数图象,其中: 的函数解析式为 . 假设两种灯的使用寿命都是2000小时,照明效果一样. (1)、根据图象直接写出 的函数关系式;(2)、小军认为节能灯一定比白炽灯省钱,你认为呢?23. 已知:如图1,是直角三角形, , 的角平分线与的垂直平分线相交于点 .
(1)、根据图象直接写出 的函数关系式;(2)、小军认为节能灯一定比白炽灯省钱,你认为呢?23. 已知:如图1,是直角三角形, , 的角平分线与的垂直平分线相交于点 . (1)、如图2,若点正好落在边上,求的度数;(2)、如图3,若点满足、、共线,线段、、之间是否满足 , 若满足请给出证明;若不满足,请说明理由.24. 今年1月,市地铁价格实行消费累计优惠.普通成人每月持卡乘坐地铁,当消费累计金额不超过150元时,每次乘坐地铁的票价打9.5折;当消费累计金额超过150元时,达到规定的消费累计金额后的乘次,票价所打折扣如下表所示:
(1)、如图2,若点正好落在边上,求的度数;(2)、如图3,若点满足、、共线,线段、、之间是否满足 , 若满足请给出证明;若不满足,请说明理由.24. 今年1月,市地铁价格实行消费累计优惠.普通成人每月持卡乘坐地铁,当消费累计金额不超过150元时,每次乘坐地铁的票价打9.5折;当消费累计金额超过150元时,达到规定的消费累计金额后的乘次,票价所打折扣如下表所示:消费累计金额(元)
折扣
9折
8折
7.5折
小明上、下班每次乘坐的地铁单程票价为10元,今年3月份他上、下班持卡共乘坐了40次.
(1)、请根据以上信息填表:第1次
第2次
…
第15次
第16次
第17次
…
消费累计金额(元)
9.5
19
…
142.5
152
…
(2)、小明当月第几次乘车后,消费累计金额超过200元?(用一元一次不等式解决问题)(3)、小明3月份上、下班持卡乘坐地铁的消费累计金额为多少元?25. 已知:在中, , , 将绕点顺时针旋转一定的角度得到 , 点、的对应点分别是、 .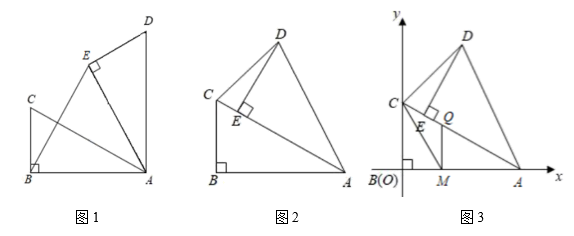 (1)、如图1,若时,连接 , 求证:;(2)、如图2,当点恰好在上时,求的度数;(3)、如图3,点、的坐标分别是 , , 点是线段上的一个动点,点是线段上的一个动点,是否存在这样的点、使得为等腰三角形且为直角三角形?若存在,请求出满足条件的点的坐标;若不存在,请说明理由.
(1)、如图1,若时,连接 , 求证:;(2)、如图2,当点恰好在上时,求的度数;(3)、如图3,点、的坐标分别是 , , 点是线段上的一个动点,点是线段上的一个动点,是否存在这样的点、使得为等腰三角形且为直角三角形?若存在,请求出满足条件的点的坐标;若不存在,请说明理由.