广东省广州市南沙区2020-2021学年八年级下学期期中数学试题
试卷更新日期:2022-03-10 类型:期中考试
一、单选题
-
1. 式子在实数范围内有意义,则的取值范围是( )A、 B、 C、 D、2. 下列各组线段中,能组成直角三角形的一组是( )A、1,2,3 B、2,3,4 C、3,5,6 D、1, , 23.
如图,已知两正方形的面积分别是25和169,则字母B所代表的正方形的面积是( )
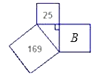 A、12 B、13 C、144 D、1944. 如图,数轴上点A对应的数为2,AB⊥OA于A,且AB=1,以OB为半径画圆,交数轴于点C,则OC的长为( )
A、12 B、13 C、144 D、1944. 如图,数轴上点A对应的数为2,AB⊥OA于A,且AB=1,以OB为半径画圆,交数轴于点C,则OC的长为( )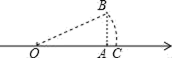 A、3 B、 C、 D、5. 下列二次根式化简后与能合并的是( )A、 B、 C、 D、6. 下列式子中,属于最简二次根式的是( )A、 B、 C、 D、7. 下列各命题都成立,而它们的逆命题不能成立的是( ).A、两直线平行,同位角相等 B、全等三角形的对应角相等 C、四边相等的四边形是菱形 D、直角三角形中, 斜边的平方等于两直角边的平方和8. 如图,在平行四边形ABCD中,对角线 相交于点 , , 若要使平行四边形ABCD为矩形,则 的长应该为( )
A、3 B、 C、 D、5. 下列二次根式化简后与能合并的是( )A、 B、 C、 D、6. 下列式子中,属于最简二次根式的是( )A、 B、 C、 D、7. 下列各命题都成立,而它们的逆命题不能成立的是( ).A、两直线平行,同位角相等 B、全等三角形的对应角相等 C、四边相等的四边形是菱形 D、直角三角形中, 斜边的平方等于两直角边的平方和8. 如图,在平行四边形ABCD中,对角线 相交于点 , , 若要使平行四边形ABCD为矩形,则 的长应该为( )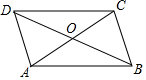 A、4 B、3 C、2 D、19. 如图,在△ABC中,BD,CE是△ABC的中线,BD与CE相交于点O,点F,G分别是BO,CO的中点,连接AO.若AO=6cm,BC=8cm,则四边形DEFG的周长是( )
A、4 B、3 C、2 D、19. 如图,在△ABC中,BD,CE是△ABC的中线,BD与CE相交于点O,点F,G分别是BO,CO的中点,连接AO.若AO=6cm,BC=8cm,则四边形DEFG的周长是( )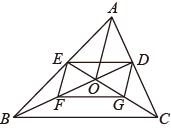 A、14cm B、18cm C、24cm D、28cm10.
A、14cm B、18cm C、24cm D、28cm10.如图,将等边△ABC沿射线BC向右平移到△DCE的位置,连接AD、BD,则下列结论:
①AD=BC;②BD、AC互相平分;③四边形ACED是菱形;④BD⊥DE.
其中正确的个数是( )
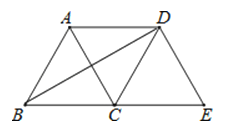 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
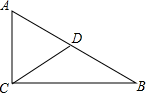
11. 若▱ABCD中,∠A=50°,则∠C=°.12. 如图,在Rt中,∠ACB=90°,点D是AB的中点,AC=6 , BC=8,则CD= .
 13. 如图,已知四边形ABCD,对角线AC和BD相交于O,已知AB∥CD,则添加一个条件可得出四边形ABCD是平行四边形.
13. 如图,已知四边形ABCD,对角线AC和BD相交于O,已知AB∥CD,则添加一个条件可得出四边形ABCD是平行四边形.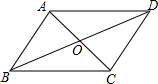 14. 一个三角形的三边长分别是 , 则它的周长为 .15. 如图,直线经过正方形的顶点 , 分别过正方形的顶点、作于点 , 于点 , 若 , , 则的长为 .
14. 一个三角形的三边长分别是 , 则它的周长为 .15. 如图,直线经过正方形的顶点 , 分别过正方形的顶点、作于点 , 于点 , 若 , , 则的长为 .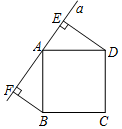 16. 实数在数轴上的位置如图所示,则化简的结果是 .
16. 实数在数轴上的位置如图所示,则化简的结果是 .
三、解答题
-
17. 计算:(1)、;(2)、 .18.
如图:在▱ABCD中,∠BAD的平分线A E交DC于E,若∠DAE=25°,求∠C、∠B的度数.
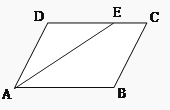 19. 如图,在▱ABCD中,点E、F分别在AD、BC上,且AE=CF.求证:四边形BFDE是平行四边形.
19. 如图,在▱ABCD中,点E、F分别在AD、BC上,且AE=CF.求证:四边形BFDE是平行四边形.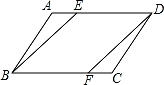 20. 如图,四边形ABCD中,AB=10,BC=13,CD=12,AD=5,AD⊥CD,求四边形ABCD的面积.
20. 如图,四边形ABCD中,AB=10,BC=13,CD=12,AD=5,AD⊥CD,求四边形ABCD的面积.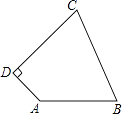 21. 已知: , 求下列各式的值:(1)、;(2)、 .22. 如图,矩形ABCD的对角线AC、BD相交于点O, AE⊥BD于E,CF⊥BD于F.
21. 已知: , 求下列各式的值:(1)、;(2)、 .22. 如图,矩形ABCD的对角线AC、BD相交于点O, AE⊥BD于E,CF⊥BD于F.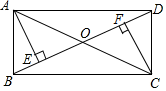 (1)、求证:AE=CF;(2)、若AB=6,∠COD=60°,求矩形ABCD的面积.23. 已知: ▱ ABCD中,对角线AC与BD相交于点O.
(1)、求证:AE=CF;(2)、若AB=6,∠COD=60°,求矩形ABCD的面积.23. 已知: ▱ ABCD中,对角线AC与BD相交于点O.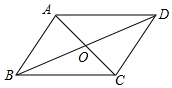 (1)、尺规作图:作对角线BD的垂直平分线EF,分别交AD、BC于E、F;(2)、连接BE、DF,求证:四边形EBFD为菱形.24. 如图,在 中, , 过点 的直线MN//AB,为 边上一点,过点 作 , 垂足为点 , 交直线 于点 , 连接 , .
(1)、尺规作图:作对角线BD的垂直平分线EF,分别交AD、BC于E、F;(2)、连接BE、DF,求证:四边形EBFD为菱形.24. 如图,在 中, , 过点 的直线MN//AB,为 边上一点,过点 作 , 垂足为点 , 交直线 于点 , 连接 , . (1)、求证:;(2)、当为中点时,四边形 是什么特殊四边形?说明你的理由;(3)、在()的条件下,当 的大小满足什么条件时,四边形 是正方形?请说明你的理由.25. 已知:正方形ABCD,点P是对角线AC所在直线上的动点,点E在DC边所在的直线上,且随着点P的运动而运动,PE=PD总成立.
(1)、求证:;(2)、当为中点时,四边形 是什么特殊四边形?说明你的理由;(3)、在()的条件下,当 的大小满足什么条件时,四边形 是正方形?请说明你的理由.25. 已知:正方形ABCD,点P是对角线AC所在直线上的动点,点E在DC边所在的直线上,且随着点P的运动而运动,PE=PD总成立.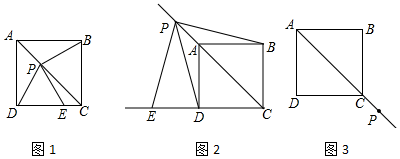 (1)、如图1,当点P在对角线AC上时,请你猜想PE与PB有怎样的数量关系,并加以证明;(2)、如图2,当点P运动到CA的延长线上时,(1)中猜想的结论是否成立?如果成立,请给出证明;如果不成立,请说明理由;(3)、如图2,当点P运动到CA的反向延长线上时,请你利用图3画出满足条件的图形,并判断此时PE与PB有怎样的关系?(直接写出结论不必证明)
(1)、如图1,当点P在对角线AC上时,请你猜想PE与PB有怎样的数量关系,并加以证明;(2)、如图2,当点P运动到CA的延长线上时,(1)中猜想的结论是否成立?如果成立,请给出证明;如果不成立,请说明理由;(3)、如图2,当点P运动到CA的反向延长线上时,请你利用图3画出满足条件的图形,并判断此时PE与PB有怎样的关系?(直接写出结论不必证明)