安徽省宣城市宣州区2020-2021学年八年级下学期期中数学试题

试卷更新日期：2022-03-10 类型：期中考试

进入出卷网下载

一、单选题

1. 下列方程中属于一元二次方程的是（）

A、 $\frac{1}{x^{2}} + \frac{1}{x} = 0$ B、x²+3x = x²-2 C、ax²+bx+c = 0 D、2( x+1)² = x+1

查看试题解析
2. 已知实数x、y满足 $\sqrt{2 x - 3 y + 1}$ ＋|x﹣3y﹣2|＝0，则xy的平方根是（）

A、 $\sqrt{5}$ B、± $\sqrt{5}$ C、 $\sqrt{6}$ D、± $\sqrt{6}$

查看试题解析
3. 下列四组线段中，可以构成直角三角形的是（　　）

A、4，5，6 B、1.5，2，2.5 C、2，3，4 D、1， $\sqrt{2}$ ， 3

查看试题解析
4. 若关于x的一元二次方程mx²﹣4x+3＝0有实数根，则m的取值范围是（）

A、m≤2 B、m≠0 C、m≤ $\frac{4}{3}$ 且m≠0 D、m＜2

查看试题解析
5. 已知 $\sqrt{18 n}$ 是正整数，则实数n的最小值是（）

A、3 B、2 C、1 D、 $\frac{1}{18}$

查看试题解析
6. 下列二次根式中，是最简二次根式的是（）

A、 $\sqrt{18}$ B、 $\sqrt{13}$ C、 $\sqrt{27}$ D、 $\sqrt{12}$

查看试题解析
7. 实数a，b在数轴上的位置如图所示，则化简 $\sqrt{（ a - 1 ）^{2}}$ - $\sqrt{（ a - b ）^{2}}$ +b的结果是（　　）

A、1 B、b+1 C、2a D、1-2a

查看试题解析
8. △ABC的三边为a，b，c且（a＋b）（a﹣b）＝c² ，则该三角形是（）

A、锐角三角形 B、以c为斜边的直角三角形 C、以b为斜边的直角三角形 D、以a为斜边的直角三角形

查看试题解析
9. 下列选项中，不能判定四边形ABCD是平行四边形的是 $($ 　　 $)$

A、 $AD / / BC$ ， $AB / / CD$ B、 $AB / / CD$ ， $AB = CD$ C、 $AD / / BC$ ， $AB = DC$ D、 $AB = DC$ ， $AD = BC$

查看试题解析
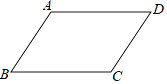10. 在一幅长80cm，宽50cm的矩形风景画的四周镶一条金色纸边，制成一幅矩形挂图，如图所示，如果要使整个挂图的面积是5400cm² ，设金色纸边的宽为xcm，那么x满足的方程是（）

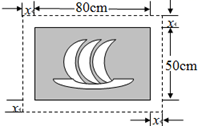A、x²+65x-350=0 B、x²+130x-1400=0 C、x²-130x-1400=0 D、x²-65x-350=0

查看试题解析

二、填空题

11. 使 $\sqrt{x + 1}$ 有意义的x的取值范围是．

查看试题解析
12. 比较大小：3²2³ ．

查看试题解析
13. 设S＝ $\sqrt{1 + \frac{1}{1^{2}} + \frac{1}{2^{2}}}$ ＋ $\sqrt{1 + \frac{1}{2^{2}} + \frac{1}{3^{2}}}$ ＋ $\sqrt{1 + \frac{1}{3^{2}} + \frac{1}{4^{2}}}$ ＋…＋ $\sqrt{1 + \frac{1}{201 9^{2}} + \frac{1}{202 0^{2}}}$ ，则S的整数部分是．

查看试题解析
14. 定义新运算“ $\oplus$ ”的运算法则为： $x \oplus y = \sqrt{x y + 4}$ ，则 $(2 \oplus 6) \oplus 8$ = ．

查看试题解析

三、解答题

15. 计算：

(1)、 $\sqrt{8} - \frac{1}{3} \sqrt{18}$

(2)、 $\sqrt{27} \div \sqrt{3} - \sqrt{20} \times \sqrt{5}$

查看试题解析
16. 解方程：

(1)、 $x^{2} = 4 x$ （因式分解法）

(2)、 $2 x^{2} - 4 x - 3 = 0$ （公式法）

查看试题解析
17. 新型冠状病毒具有很强的传染性，大家平时一定要注重个人防护，若有一人感染上新冠病毒，经过两轮传染后，共有100人患病，则每轮传染中平均一个人传染多少人？（假设每轮传染中，平均一个人传染的人数相同，请列方程解应用题）

查看试题解析
18. 如图，在四边形ABCD中，∠ABC＝30°，∠ADC＝60°，AD＝DC．
证明：BD²＝AB²＋BC² ．

查看试题解析
19. 阅读下面的例题：解方程 $x^{2} - | x | - 2 = 0$
解：当x≥0时，原方程化为x²－x－2＝0，解得：x₁＝2，x₂＝－1（不合题意，舍去）；

当x＜0时，原方程化为x²＋ x－2＝0，解得：x₁＝1，（不合题意，舍去）x₂＝－2；

∴原方程的根是x₁＝2，x₂＝－2.

请参照例题解方程 $x^{2} - | x - 1 | - 1 = 0$ .

查看试题解析
20. 非零实数a，b（a≠b）满足a²﹣a﹣2013＝0，b²﹣b﹣2013＝0，求 $\frac{1}{a} + \frac{1}{b}$ 的值．

查看试题解析
21. 为打造“文化九中，书香校园”，阜阳九中积极开展“图书漂流”活动，旨在让全体师生共建共享，校团委学生处在对上学期学生借阅登记簿进行统计时发现，在4月份有1000名学生借阅了名著类书籍，5月份人数比4月份增加10%，6月份全校借阅名著类书籍人数比5月份增加340人.

(1)、求6月份全校借阅名著类书籍的学生人数；

(2)、列方程求从4月份到6月份全校借阅名著类书籍的学生人数的平均增长率.

查看试题解析
22. 法国数学家费尔马早在17世纪就研究过形如x²+y²＝z²的方程，显然，这个方程有无数组解．我们把满足该方程的正整数的解（x，y，z）叫做勾股数，如（3，4，5）就是一组勾股数．

(1)、在研究勾股数时，古希腊的哲学家柏拉图曾指出：如果n表示大于1的整数，x＝2n，y＝n²﹣1，z＝n²+1，那么，以x，y，z为三边的三角形为直角三角形（即x，y，z为勾股数），请你加以证明；

(2)、探索规律：观察下列各组数（3，4，5），（5，12，13），（7，24，25），（9，40，41）…，直接写出第6个数组．

查看试题解析
23. 如图，在△ABC中，∠B=90°，AB=8厘米，BC=6厘米，P、Q是△ABC边上的两个动点，其中点P从点A开始沿A→B方向运动速度为1厘米/秒，点Q从点B开始沿B→C→A方向运动速度为2厘米/秒，若它们同时出发，设出发的时间为t秒.

(1)、求出发2秒后，PQ的长；

(2)、点Q在CA边上运动时，当△BCQ成为等腰三角形时，求点Q的运动时间.

查看试题解析