安徽省芜湖市无为市2020-2021学年八年级下学期期中数学试题

试卷更新日期：2022-03-10 类型：期中考试

进入出卷网下载

一、单选题

1. 如图，在四边形 $A B C D$ 中，已知 $A B = C D$ ，添加下列条件中的一个，不能判定四边形 $A B C D$ 是平行四边形的是（）

A、 $A B / / C D$ B、 $B C / / A D$ C、 $B C = A D$ D、 $∠ A + ∠ D = 180 °$

查看试题解析
2. 下列二次根式是最简二次根式的是（）

A、 $\sqrt{3.6}$ B、 $\sqrt{\frac{2}{3}}$ C、 $\sqrt{18}$ D、 $\sqrt{47}$

查看试题解析
3. 如图，为了测量池塘边A、B两地之间的距离，在线段AB的同侧取一点C，连接CA并延长至点D，连接CB并延长至点E，使得A、B分别是CD、CE的中点，若DE＝16m，则AB的长度是（）

A、8m B、9m C、12m D、6m

查看试题解析
4. 下列说法正确的是（）

A、矩形的对角线互相垂直平分 B、对角线分别平分对角的四边形是矩形 C、对角线相等的菱形是正方形 D、有一组邻边相等的四边形是菱形

查看试题解析
5. 若代数式 $\sqrt{m} + \frac{1}{\sqrt{- m n}}$ 有意义，则在平面直角坐标系中点 $(m ， n)$ 位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
6. 在直角三角形中，两直角边的长分别为6和12，则斜边上中线的长为（）

A、3 $\sqrt{3}$ B、3 $\sqrt{5}$ C、6 $\sqrt{3}$ D、6 $\sqrt{5}$

查看试题解析
7. 如图，在网格中，每个小正方形的边长均为1，则在△ABC中，边长为有理数的边有（）

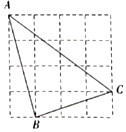A、3条 B、2条 C、1条 D、0条

查看试题解析
8. 已知实数 $a$ ， $b$ 在数轴上的位置如图所示，则化简 $| b - 1 | - \sqrt{{(a + 1)}^{2}} + \sqrt{{(a - b)}^{2}}$ 的结果为（）

A、 $2 b$ B、 $2 b - 2$ C、－2 D、 $- 2 a + 2$

查看试题解析
9. 在《算法统宗》中有一道“荡秋千”的问题：“平地秋千未起，踏板一尺离地送行二步与人齐，五尺人高曾记. 仕女佳人争蹴，终朝笑语欢嬉.良工高士素好奇，算出索长有几.”此问题可理解为：如图，有一架秋千，当它静止时，踏板离地距离 $A B$ 长度为1尺.将它往前水平推送10尺时，即 $A^{'} C$ ＝10尺，则此时秋千的踏板离地距离 $A^{'} D$ 就和身高5尺的人一样高.若运动过程中秋千的绳索始终拉得很直，则绳索 $O A$ 长为（）

A、13.5尺 B、14尺 C、14.5尺 D、15尺

查看试题解析
10. 如图，A₁ ， B₁ ， C₁ ， D₁分别是四边形ABCD各边的中点，且AC⊥BD，AC＝6，BD＝10．依次取A₁B₁ ， B₁C₁ ， C₁D₁ ， D₁A₁的中点A₂ ， B₂ ， C₂ ， D₂ ，再依次取A₂B₂ ， B₂C₂ ， C₂D₂ ， D₂A₂的中点A₃ ， B₃ ， C₃ ， D₃……以此类推取A_n﹣₁B_n﹣₁ ， B_n﹣₁C_n﹣₁ ， C_n﹣₁D_n﹣₁ ， D_n﹣₁A_n﹣₁的中点A_n ， B_n ， C_n ， D_n ，若四边形A_nB_nC_nD_n的面积为 $\frac{15}{32}$ ，则n的值为（）

A、5 B、6 C、7 D、8

查看试题解析

二、填空题

11. 若规定a⊗b＝ $\sqrt{a}$ • $\sqrt{b}$ +2 $\sqrt{\frac{a}{b}}$ ，则2⊗4的值为．

查看试题解析
12. 如图，在△ABC中，AC＝24，AB＝25，BC＝7．在AB上取一点E，AC上取一点F，连接EF，若∠EFC＝125°，过点B作BD∥EF，且点D在AB的右侧，则∠CBD的度数为．

查看试题解析
13. 如图，菱形ABCD的边长为5，对角线BD的长为8，点E，F分别是边AD，CD的中点，连接EF并延长与BC的延长线相交于点G，则EG的长为．

查看试题解析
14. 如图，在矩形纸片ABCD中，AB＝12，AD＝5，P为DC边上的动点（点P不与点D，C重合），将纸片沿AP折叠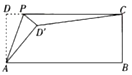

(1)、当四边形ADPD′是正方形时，CD′的长为．

(2)、当CD′的长最小时，PC的长为．

查看试题解析
15. 计算： $(\sqrt{24} - \sqrt{6}) \div \sqrt{3} =$ .

查看试题解析

三、解答题

16. 如图，在菱形ABCD中，CE＝CF.求证：AE＝AF.

查看试题解析
17. 已知 $x = \sqrt{5} + 2$ ，求代数式 $x^{2} - 4 x$ 的值．

查看试题解析
18. 如图，在正方形ABCD中，E为CD边上一点，F为AD延长线上一点，且DE＝DF，则AE与CF之间有怎样的关系？判断并说明理由．

查看试题解析
19. 如图，在△ABC中，∠C＝90°，CD＝1.8，BD＝3．

(1)、若∠2＝∠B，求AC的长．

(2)、若∠1＝∠2，求AC的长．

查看试题解析
20. 如图，在平行四边形ABCD中，点O是BC的中点，连接DO并延长，交AB延长线于点E，连接BD，EC.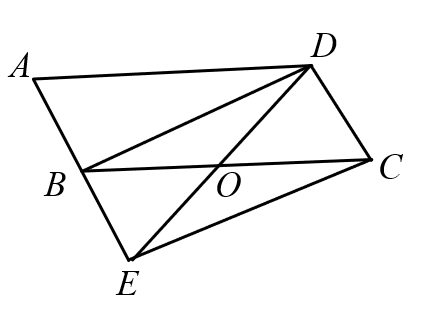

(1)、求证：四边形BECD是平行四边形；

(2)、若 $∠ A = 50 °$ ，则当 $∠ A D E =$ °时，四边形BECD是菱形.

查看试题解析
21. 已知 $m a x {\sqrt{x} ， \frac{1}{\sqrt{x} + 1} ， x - 1}$ 表示取 $\sqrt{x}$ ， $\frac{1}{\sqrt{x} + 1}$ ， $x - 1$ 三个数中最大的那个数．例如当 $x = 2$ 时， $m a x {\sqrt{x} ， \frac{1}{\sqrt{x} + 1} ， x - 1} = m a x {\sqrt{2} ， \frac{1}{\sqrt{2} + 1} = \sqrt{2} - 1 ， 1} = \sqrt{2}$ ．

(1)、当 $x = \frac{1}{4}$ 时， $m a x {\sqrt{x} ， \frac{1}{\sqrt{x} + 1} ， x - 1}$ 的值为．

(2)、当 $m a x {\sqrt{x} ， \frac{1}{\sqrt{x} + 1} ， x - 1} = 2$ 时，求 $x$ 的值．

查看试题解析
22. 小明在学完了平行四边形后，想对“四边形的不稳定性”和“四边形的判定”有更好的理解，做了如下的探究：他用8根木棍和一些钉子组成了正方形 $A B C D$ 和平行四边形 $H E F G$ （如图1），且 $B C$ ， $E F$ 在同一条直线上，点 $D$ 落在边 $H E$ 上．经小明测量，发现此时 $B$ 、 $D$ 、 $G$ 三个点在一条直线上， $∠ E F G = 67.5 °$ ， $D G = 3$ ．

(1)、求 $H G$ 的长．

(2)、设 $B C$ 的长度为 $a$ ，则 $C E =$ （用含 $a$ 的代数式表示）．

(3)、小明接着探究，在保证 $B C$ ， $E F$ 位置不变的前提条件下，从点 $A$ 向右推动正方形，直到四边形 $E F G H$ 刚好变为矩形时停止推动（如图2）．若此时 $D E^{2} = 18 (\sqrt{2} - 1)$ ，求 $B F$ 的长．

查看试题解析
23. 如图所示的是与菱形有关的三个图形．

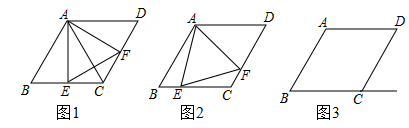(1)、如图1，AC是菱形ABCD的对角线，∠B＝60°，E、F分别是边BC、CD上的中点，连接AE、EF、AF．若AC＝3，则CE+CF的长为．

(2)、如图2，在菱形ABCD中，∠B＝60°．E是边BC上的点，连接AE，作∠EAF＝60°，边AF交边CD于点F，连接EF．若BC＝3，求CE+CF的长．

(3)、在菱形ABCD中，∠B＝60°，E是边BC延长线上的点，连接AE，作∠EAF＝60°，边AF交边CD的延长线于点F，连接EF．当BC＝3，EF⊥BC时，在图3中，将图形补充完整并求△AEF的周长．

查看试题解析