安徽省淮南市西部地区2020-2021学年八年级下学期期中数学试题

试卷更新日期：2022-03-10 类型：期中考试

进入出卷网下载

一、单选题

1. 计算 $(- \sqrt{2})^{2}$ 的结果是（）

A、﹣4 B、﹣2 C、2 D、4

查看试题解析
2. 在Rt△ABC中，∠C=90°，a=1，c=2，则b的长是（）

A、1 B、 $\sqrt{3}$ C、2 D、 $\sqrt{5}$

查看试题解析
3. 已知 $▱$ ABCD，∠A+∠C＝260°，则∠B的度数是（）

A、50° B、60° C、130° D、160°

查看试题解析
4. 估计 $\sqrt{12} \times \sqrt{\frac{1}{3}} + \sqrt{6} \div \sqrt{2}$ 的运算结果最接近的整数是（）

A、2 B、3 C、4 D、5

查看试题解析
5. 下列说法，不正确的是（）

A、有一个角是直角的平行四边形是矩形 B、两条对角线相等的菱形是正方形 C、一组对边平行且相等的四边形是平行四边形 D、两条对角线互相垂直的四边形是菱形

查看试题解析
6. 如图，在平面直角坐标系中，A（4，0），B（0，3），以点A为圆心，AB长为半径画弧，交x轴的负半轴于点P，则P的坐标为（）

A、（﹣1，0） B、（﹣5，0） C、（1，0） D、（0，﹣1）

查看试题解析
7. 实数a，b在数轴上对应点的位置如图，则化简 $\sqrt{a^{2}} + | a + b |$ 的结果为（）

A、2a﹣b B、2a+b C、b D、﹣2a+b

查看试题解析
8. 如图，菱形ABCD中，对角线AC ， BD相交于点O ， E为AB的中点．若菱形ABCD的周长为32，则OE的长为（）

A、3 B、4 C、5 D、6

查看试题解析
9. 如图，在▱ABCD中，对角线AC，BD相交于点O，E是BC的中点，以下说法不正确的是（）

A、CD＝2OE B、OA＝OC C、∠BOE＝∠OBA D、∠OBE＝∠OCE

查看试题解析
10. 如图，正方形ABCD的边AB上有一动点E，以EC为边作矩形ECFG，且边FG过点D．在点E从点A移动到点B的过程中，矩形ECFG的面积（）

A、先变大后变小 B、保持不变 C、一直变大 D、一直变小

查看试题解析

二、填空题

11. 使 $\sqrt{x + 1}$ 有意义的x的取值范围是．

查看试题解析
12. 请写出命题“直角三角形的两个锐角互余”的逆命题：．

查看试题解析
13. 在四边形ABCD中，BD是对角线，∠ABD＝∠CDB，要使四边形ABCD是平行四边形只需添加一个条件，这个条件可以是(只需写出一种情况)．

查看试题解析
14. 直角三角形的两边长分别是3和4，则此三角形的面积是

查看试题解析
15. 如图，在矩形ABCD中，AC、BD交于点O，DE⊥AC于点E，若∠AOD＝110°，则∠CDE＝°.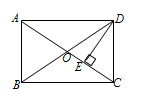

查看试题解析
16. 为了比较 $\sqrt{5}$ +1与 $\sqrt{10}$ 的大小，可以构造如图所示的图形进行推算，其中∠C=90°，BC=3，D在BC上且BD=AC=1．通过计算可得 $\sqrt{5}$ +1 $\sqrt{10}$ ．（填“＞”或“＜”或“=”）

查看试题解析
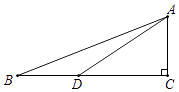17. 一架长为10m的梯子，斜靠在竖直的墙上，这时梯子的底端与墙的距离为6m，如果梯子顶端沿墙下滑2m，那么梯子底端将滑动m．

查看试题解析
18. 如图，有一正方形纸片ABCD，先将正方形ABCD对折，设折痕为EF，再沿过点C的折痕将角B翻折，使得点B落在EF的H上，折痕交BE于点G，则∠HCF的度数为；若正方形ABCD的边长为2，则EG的长度为．

查看试题解析

三、解答题

19.

(1)、计算： $(\sqrt{3} + \sqrt{8}) \times \sqrt{6} - 4 \sqrt{\frac{1}{2}}$ ；

(2)、计算： $(\sqrt{2} - 1)^{2} - (\sqrt{2} - 1) (1 + 2 \sqrt{2})$ ；

(3)、若 $a = \sqrt{b - 5} + \sqrt{5 - b} + 4$ ，求a﹣b的值．

查看试题解析
20. 如图，在平面直角坐标系中，A（2，2），B（﹣2，﹣1），C（0，﹣2）．

(1)、请直接写出△ABC的面积为；

(2)、若以A，B，C及点D为顶点的四边形为平行四边形，试画出其中一个平行四边形，并写出所画平行四边形中D点的坐标 ▲ ．

查看试题解析
21. 如图，平行四边形ABCD的对角线AC与BD相交于点O，点E为AO的中点，过点A作AF∥BD交BE的延长线于点F，连接DF.

(1)、求证：四边形AODF是平行四边形；

(2)、填空：
①当△ACD满足条件时，四边形AODF是菱形.

②当△ACD满足条件时，四边形AODF是矩形.

查看试题解析
22. 在学习“勾股数”的知识时，爱动脑的小明设计了如下表格：
n
2
3
4
5
6
....
a
4
5
8
10
12
.....
b
3
8
15
24
35
.....
c
5
10
17
26
37
......
请回答下列问题：

(1)、当n＝7时，a＝， b＝， c＝；

(2)、请你分别观察a，b，c与n之间的关系，并用含自然数n（n＞1）的代数式表示：a＝， b＝， c＝；

(3)、猜想：以a，b，c为边长的三角形是否为直角三角形？并对你的猜想加以证明．

查看试题解析
23. 请认真完成下列数学活动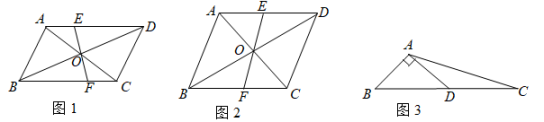
典例再现：如图1，▱ABCD的对线AC，BD相交于点O，EF过点O且与AD，BC分别相交于点E，F．求证：OE＝OF．

(1)、尝试发现
按图1填空：
①若▱ABCD的周长是24，OE＝2，则四边形ABFE的周长为；
②若▱ABCD的面积是20，则四边形ABFE的面积是．

(2)、应用发现
如图2，在菱形ABCD中，对角线相交于点O，过点O的直线分别交AD，BC于点E，F．若AC＝ $4 \sqrt{3}$ ， AD＝6，求四边形ABFE的面积．

(3)、应用拓展
如图3，在△ABC中，点D是BC的中点，连接AD，若∠BAD＝90°，AB＝2，AC＝ $2 \sqrt{5}$ ，则△ABC的面积是．

查看试题解析

n	2	3	4	5	6	....
a	4	5	8	10	12	.....
b	3	8	15	24	35	.....
c	5	10	17	26	37	......