安徽省合肥市包河区2020-2021学年八年级下学期期中数学试题
试卷更新日期：2022-03-10 类型：期中考试
一、单选题
-
1. 一元二次方程x2＝3x的解为（ ）A、x＝0 B、x＝3 C、x＝0或x＝3 D、x＝0 且x＝32. 下列整数中，与 最接近的整数是（ ）.A、3 B、4 C、5 D、63. 下列运算正确的是（ ）A、 B、 C、 D、4. 方程x2+3x﹣1＝0的两根为x1 ， x2 ， 则x1+x2等于（ ）A、﹣1 B、1 C、﹣3 D、35. 下列各组数是勾股数的为（ ）A、2，4，5 B、8，15，17 C、11，13，15 D、4，5，66. 用配方法解一元二次方程x2﹣6x﹣5=0，此方程可化为（ ）A、（x﹣3）2=4 B、（x﹣3）2=14 C、（x﹣9）2=4 D、（x﹣9）2=147. 一个圆桶底面直径为7cm，高24cm，则桶内所能容下的最长木棒为（ ）A、20cm B、25cm C、26cm D、30cm8. 已知关于x的一元二次方程(m－1)x2＋2x＋1＝0有实数根，则m的取值范围是（ ）A、m＜2 B、m≤2 C、m＜2且m≠1 D、m≤2且m≠19. 已知A点坐标为A（）点B在直线y＝﹣x上运动，当线段AB最短时，B点坐标（ ）A、（0，0） B、（ ， ﹣） C、（1，﹣1） D、（﹣ ， ）10. 如图，ABCD是一张长方形纸片，将AD，BC折起，使A、B两点重合于CD边上的P点，然后压平得折痕EF与GH．若PE＝8cm，PG＝6cm，EG＝10cm，则长方形纸片ABCD的面积为（ ）
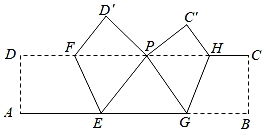A、105.6cm2 B、110.4cm2 C、115.2cm2 D、124.8cm2二、填空题
-
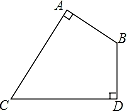
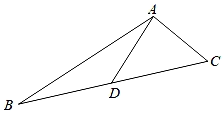
11. 已知一个多边形的内角和为540°，则这个多边形是边形．12. 计算： 的结果是 ．13. 某种品牌运动服经过两次降价，每件零售价由560元降为315元，已知两次降价的百分率相同，求每次降价的百分率．设每次降价的百分率为x，所列方程是 ．14. 计算： 的结果是 ．15. 若实数a、b满足|a2+3|+＝3．则a+b＝ ．16. 如图，△ABC中，AB＝13，AD＝6，AC＝5，D为BC边的中点．则S△ABC＝ ．
17. 如图，四边形ABCD中，AD∥BC，∠D＝90°，M是AB的中点，若CM＝6.5，BC+CD+DA＝17，则四边形ABCD的面积为 ．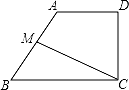
三、解答题
-
18. 选择合适的方法解方程：(1)、2（x+3）2＝18；(2)、3x2﹣6x﹣4＝0．19. 关于x的一元二次方程mx2﹣（2m﹣3）x+（m﹣1）=0有两个实数根．(1)、求m的取值范围；(2)、若m为正整数，求此方程的根．20. 2020年疫情期间，某区推出名师公益大课堂，为学生提供线上线下免费辅导，据统计，第一批公益课受益学生2万人次，第三批公益课受益学生2.42万人次．(1)、如果第二批，第三批公益课受益学生人次的增长率相同，求这个增长率；(2)、按照这个增长率，预计第四批公益课受益学生将达到多少万人次？21. 为提高公司经济效益，某公司决定对近期研发出的一种电子产品进行降价促销，使生产的电子产品能够及时售出．根据市场调查：这种电子产品销售单价定为200元时，每天可售出300个；若销售单价每降低5元，每天可多售出25个．已知每个电子产品的固定成本为100元．问这种电子产品降价后的销售单价为多少元时，公司每天可获利32000元？
