安徽省阜阳市阜南县2020-2021学年八年级下学期期中数学试题
试卷更新日期:2022-03-10 类型:期中考试
一、单选题
-
1. 下列二次根式是最简二次根式的为( )A、 B、 C、 D、2. 下列方程中,是一元二次方程的是( )A、 B、 C、 D、3. 下面几组数能作为直角三角形三边长的是( )A、2,4,5 B、5,12,13 C、12,18,22 D、4,5,84. 如图,数轴上的点A表示的数是-2,点B表示的数是1,于点B,且 , 以点A为圆心,AC为半径画弧交数轴于点D,则点D表示的数为( )
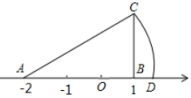 A、 B、 C、 D、25. 用配方法解一元二次方程 , 下列变形正确的的是( )A、 B、 C、 D、6. 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中 , , , , 则下列判断不正确的是( )
A、 B、 C、 D、25. 用配方法解一元二次方程 , 下列变形正确的的是( )A、 B、 C、 D、6. 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中 , , , , 则下列判断不正确的是( ) A、 B、 C、 D、7. 关于x的一元二次方程根的情况,下列说法正确的是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根. D、无法确定8. 如图所示,将正六边形与正五边形按此方式摆放,正六边形与正五边形的公共顶点为O,且正六边形的边AB与正五边形的边DE共线,则∠COF的度数是( )
A、 B、 C、 D、7. 关于x的一元二次方程根的情况,下列说法正确的是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根. D、无法确定8. 如图所示,将正六边形与正五边形按此方式摆放,正六边形与正五边形的公共顶点为O,且正六边形的边AB与正五边形的边DE共线,则∠COF的度数是( ) A、86° B、84° C、76° D、74°9. 如图,若每个小方格的面积为1,则图中以格点为端点且长度为 的线段有( )
A、86° B、84° C、76° D、74°9. 如图,若每个小方格的面积为1,则图中以格点为端点且长度为 的线段有( )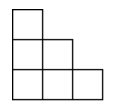 A、2条 B、3条 C、4条 D、5条10. 如图,要在一块长20米、宽15米的矩形地面上,修建了三条宽度相等的道路(其中两条路与宽平行,一条路与长平行)。若要使剩余部分的面积为208平方米,则道路的宽为( )米
A、2条 B、3条 C、4条 D、5条10. 如图,要在一块长20米、宽15米的矩形地面上,修建了三条宽度相等的道路(其中两条路与宽平行,一条路与长平行)。若要使剩余部分的面积为208平方米,则道路的宽为( )米 A、1 B、2 C、3 D、2.5
A、1 B、2 C、3 D、2.5二、填空题
-
11. 已知一元二次方程的一个根是-1,则m的值为 .12. 《算学宝鉴》中记载了我国南宋数学家杨辉提出的一个问题:“直田积八百六十四步,之云阔不及长一十二步,问阔及长各几步?”译文:“一个矩形田地的面积等于864平方步,且它的宽比长少12步,问长与宽各是几步?”若设矩形田地的长为x步,则可列方程为 .13. 在数学课上,老师将一长方形纸片的长增加 , 宽增加 , 就成为了一个面积为的正方形,则原长方形纸片的面积为 .14. 如图,等腰 中, , , 于D,且 .则 .

三、解答题
-
15. 根据要求解下列一元二次方程.(1)、(配方法);(2)、(公式法).16. 如图,在平面直角坐标系中,已知点 , , , 连接 .
 (1)、在图中画出点A关于y轴的对称点A′,连接 , ;(2)、在(1)的基础上,试判断的形状,并说明理由.17. 一个多边形的内角和是外角和的3倍.(1)、求这个多边形的边数;(2)、这个多边形一共有多少条对角线?18. 《城市交通管理条例》规定:小汽车在城市街路上的行驶速度不得超过70千米/时.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到车速检测仪正前方30米的处,过了2秒后,小汽车行驶至处,若小汽车与观测点间的距离为50米,请通过计算说明:这辆小汽车是否超速?
(1)、在图中画出点A关于y轴的对称点A′,连接 , ;(2)、在(1)的基础上,试判断的形状,并说明理由.17. 一个多边形的内角和是外角和的3倍.(1)、求这个多边形的边数;(2)、这个多边形一共有多少条对角线?18. 《城市交通管理条例》规定:小汽车在城市街路上的行驶速度不得超过70千米/时.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到车速检测仪正前方30米的处,过了2秒后,小汽车行驶至处,若小汽车与观测点间的距离为50米,请通过计算说明:这辆小汽车是否超速? 19. 如图,有一张边长为 的正方形纸板,现将该纸板的四个角剪掉,制作一个有底无盖的长方体盒子,剪掉的四个角是面积相等的小正方形,此小正方形的边长为3 .求:
19. 如图,有一张边长为 的正方形纸板,现将该纸板的四个角剪掉,制作一个有底无盖的长方体盒子,剪掉的四个角是面积相等的小正方形,此小正方形的边长为3 .求: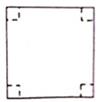 (1)、剪掉四个角后,制作长方体盒子的纸板的面积;(2)、长方体盒子的体积.20. 解方程时,我们将作为一个整体,设 , 则原方程化为 .
(1)、剪掉四个角后,制作长方体盒子的纸板的面积;(2)、长方体盒子的体积.20. 解方程时,我们将作为一个整体,设 , 则原方程化为 .解得 , .
当时, , 解得 , .
当时, , 解得 , .
所以原方程的解为 , , , .
模仿材料中解方程的方法,求方程的解.
21. 先来看一个有趣的现象: , 这里根号里的因数2经过适当的演变,2竟“跑”到了根号的外面,我们不妨把这种现象称为“穿墙”,具有这一性质的数还有许多,如:、等等.(1)、请你写一个有“穿墙”现象的数,并验证;(2)、你能只用一个正整数来表示含有上述规律的等式吗?证明你找到的规律.22. 某扶贫单位为了提高贫困户的经济收入,购买了33m的铁栅栏,准各用这些铁栅栏为贫困户靠墙(墙长15m)围建一个中间带有铁栅栏的矩形养鸡场(如图所示), (1)、若要建的矩形养鸡场面积为90m2 , 求鸡场的长(AB)和宽(BC);(2)、该扶贫单位想要建一个100m2的矩形养鸡场,这一想法能实现吗?请说明理由.23. 如图,在中, , , , P、Q是的边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒 , 点Q从点B开始沿B→C→A方向运动,且速度为每秒 , 它们同时出发,设出发的时间为t s.
(1)、若要建的矩形养鸡场面积为90m2 , 求鸡场的长(AB)和宽(BC);(2)、该扶贫单位想要建一个100m2的矩形养鸡场,这一想法能实现吗?请说明理由.23. 如图,在中, , , , P、Q是的边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒 , 点Q从点B开始沿B→C→A方向运动,且速度为每秒 , 它们同时出发,设出发的时间为t s. (1)、;(2)、当t为何值时,点P在边的垂直平分线上?(3)、当点Q在边上运动时,求出使成为等腰三角形的t值.
(1)、;(2)、当t为何值时,点P在边的垂直平分线上?(3)、当点Q在边上运动时,求出使成为等腰三角形的t值.