山东省日照市2021年中考真题数学试卷
试卷更新日期:2022-03-10 类型:中考真卷
一、单选题
-
1. 在下列四个实数中,最大的实数是( )A、-2 B、 C、 D、02. 在平面直角坐标系中,把点向右平移两个单位后,得到对应点的坐标是( )A、 B、 C、 D、3. 实验测得,某种新型冠状病毒的直径是120纳米(1纳米米),120纳米用科学记数法可表示为( )A、米 B、米 C、米 D、米4. 袁隆平院士被誉为“世界杂交水稻之父”,他研究的水稻,不仅高产,而且抗倒伏.在某次实验中,他的团队对甲、乙两种水稻品种进行产量稳定实验,各选取了8块条件相同的试验田,同时播种并核定亩产,结果甲、乙两种水稻的平均产量均为1200千克/亩,方差为 , . 为保证产量稳定,适合推广的品种为( )A、甲 B、乙 C、甲、乙均可 D、无法确定5. 下列运算正确的是( )A、 B、 C、 D、6. 一张水平放置的桌子上摆放着若干个碟子,其三视图如图所示,则这张桌子上共有碟子的个数为( )
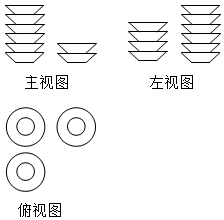 A、10 B、12 C、14 D、187. 若不等式组的解集是 , 则m的取值范围是( )A、 B、 C、 D、8. 下列命题:①的算术平方根是2;②菱形既是中心对称图形又是轴对称图形;②天气预报说明天的降水概率是 , 则明天一定会下雨;④若一个多边形的各内角都等于 , 则它是正五边形,其中真命题的个数是( )A、0 B、1 C、2 D、39. 如图,平面图形由直角边长为1的等腰直角和扇形组成,点在线段AB上, , 且交或交于点 . 设 , 图中阴影部分表示的平面图形(或)的面积为 , 则函数关于的大致图象是( )
A、10 B、12 C、14 D、187. 若不等式组的解集是 , 则m的取值范围是( )A、 B、 C、 D、8. 下列命题:①的算术平方根是2;②菱形既是中心对称图形又是轴对称图形;②天气预报说明天的降水概率是 , 则明天一定会下雨;④若一个多边形的各内角都等于 , 则它是正五边形,其中真命题的个数是( )A、0 B、1 C、2 D、39. 如图,平面图形由直角边长为1的等腰直角和扇形组成,点在线段AB上, , 且交或交于点 . 设 , 图中阴影部分表示的平面图形(或)的面积为 , 则函数关于的大致图象是( ) A、
A、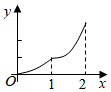 B、
B、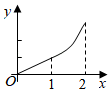 C、
C、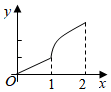 D、
D、 10. 如图,在一次数学实践活动中,小明同学要测量一座与地面垂直的古塔 的高度,他从古塔底部点B处前行 到达斜坡 的底部点C处,然后沿斜坡 前行 到达最佳测量点D处,在点D处测得塔顶A的仰角为 ,已知斜坡的斜面坡度 ,且点A,B,C,D,E在同一平面内,小明同学测得古塔 的高度是( )
10. 如图,在一次数学实践活动中,小明同学要测量一座与地面垂直的古塔 的高度,他从古塔底部点B处前行 到达斜坡 的底部点C处,然后沿斜坡 前行 到达最佳测量点D处,在点D处测得塔顶A的仰角为 ,已知斜坡的斜面坡度 ,且点A,B,C,D,E在同一平面内,小明同学测得古塔 的高度是( ) A、 B、 C、 D、11. 抛物线 的对称轴是直线 ,其图象如图所示.下列结论:① ;② ;③若 和 是抛物线上的两点,则当 时, ;④抛物线的顶点坐标为 ,则关于 的方程 无实数根.其中正确结论的个数是( )
A、 B、 C、 D、11. 抛物线 的对称轴是直线 ,其图象如图所示.下列结论:① ;② ;③若 和 是抛物线上的两点,则当 时, ;④抛物线的顶点坐标为 ,则关于 的方程 无实数根.其中正确结论的个数是( ) A、4 B、3 C、2 D、112. 数学上有很多著名的猜想,“奇偶归一猜想”就是其中之一,它至今未被证明,但研究发现,对于任意一个小于的正整数,如果是奇数,则乘3加1;如果是偶数,则除以2,得到的结果再按照上述规则重复处理,最终总能够得到1.对任意正整数 , 按照上述规则,恰好实施5次运算结果为1的所有可能取值的个数为( )A、8 B、6 C、4 D、3
A、4 B、3 C、2 D、112. 数学上有很多著名的猜想,“奇偶归一猜想”就是其中之一,它至今未被证明,但研究发现,对于任意一个小于的正整数,如果是奇数,则乘3加1;如果是偶数,则除以2,得到的结果再按照上述规则重复处理,最终总能够得到1.对任意正整数 , 按照上述规则,恰好实施5次运算结果为1的所有可能取值的个数为( )A、8 B、6 C、4 D、3二、填空题
-
13. 若式子有意义,则x的取值范围是14. 关于的方程(、为实数且),恰好是该方程的根,则的值为 .15. 如图,在矩形中, , , 点从点出发,以的速度沿BC边向点C运动,到达点停止,同时,点从点出发,以的速度沿CD边向点D运动,到达点D停止,规定其中一个动点停止运动时,另一个动点也随之停止运动.当为时,与全等.
 16. 如图,在平面直角坐标系中,正方形的边、分别在轴和轴上, , 点D是边AB上靠近点的三等分点,将沿直线折叠后得到 , 若反比例函数的图象经过点,则的值为 .
16. 如图,在平面直角坐标系中,正方形的边、分别在轴和轴上, , 点D是边AB上靠近点的三等分点,将沿直线折叠后得到 , 若反比例函数的图象经过点,则的值为 .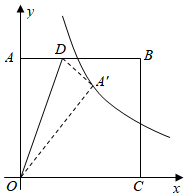
三、解答题
-
17.(1)、若单项式与单项式是一多项式中的同类项,求m、n的值;(2)、先化简,再求值: , 其中 .18. 为庆祝中国共产党建党100周年,某校加强了学生对党史知识的学习,并组织学生参加《党史知识》测试(满分100分).为了解学生对党史知识的掌握程度,从七、八年级中各随机抽取10名学生的测试成绩,进行统计、分析,过程如下:
收集数据:
七年级:86 88 95 90 100 95 95 99 93 100
八年级:100 98 98 89 87 98 95 90 90 89
整理数据:
成绩x(分)
年级
85<x≤90
90<x≤95
95<x≤100
七年级
3
4
3
八年级
5
a
b
分析数据:
统计量
年级
平均数
中位数
众数
七年级
94.1
95
d
八年级
93.4
c
98
应用数据:
(1)、填空:a- , , c= , ;(2)、若八年级共有200人参与答卷,请估计八年级测试成绩大于95分的人数;(3)、从测试成绩优秀的学生中选出5名语言表达能力较强的学生,其中八年级3名,七年级2名.现从这5名学生中随机抽取2名到当地社区担任党史宣讲员.请用画树状图或列表的方法,求恰好抽到同年级学生的概率.19. 某药店新进一批桶装消毒液,每桶进价35元,原计划以每桶55元的价格销售,为更好地助力疫情防控,现决定降价销售.已知这种消毒液销售量(桶)与每桶降价(元)()之间满足一次函数关系,其图象如图所示: (1)、求与之间的函数关系式;(2)、在这次助力疫情防控活动中,该药店仅获利1760元.这种消毒液每桶实际售价多少元?20. 如图,的对角线相交于点D,经过A、D两点,与的延长线相交于点 , 点为上一点,且 . 连接AE、DF相交于点 , 若 , .
(1)、求与之间的函数关系式;(2)、在这次助力疫情防控活动中,该药店仅获利1760元.这种消毒液每桶实际售价多少元?20. 如图,的对角线相交于点D,经过A、D两点,与的延长线相交于点 , 点为上一点,且 . 连接AE、DF相交于点 , 若 , .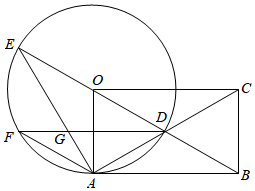 (1)、求对角线的长;(2)、求证:为矩形.21. 问题背景:
(1)、求对角线的长;(2)、求证:为矩形.21. 问题背景:如图1,在矩形中, , , 点E是边AB的中点,过点作交BD于点F.
 (1)、实验探究:
(1)、实验探究:在一次数学活动中,小王同学将图1中的绕点按逆时针方向旋转 , 如图2所示,得到结论:①;②直线AE与DF所夹锐角的度数为 .
(2)、小王同学继续将绕点B按逆时针方向旋转,旋转至如图3所示位置.请问探究(1)中的结论是否仍然成立?并说明理由.(3)、拓展延伸:在以上探究中,当旋转至、、三点共线时,则的面积为 .
22. 已知:抛物线经过 , , 三点.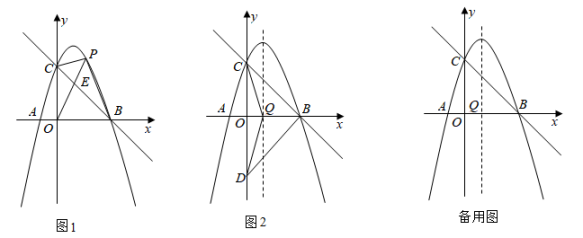 (1)、求抛物线的解析式;(2)、如图1,点为直线上方抛物线上任意一点,连、、 , 交直线于点 , 设 , 求当取最大值时点P的坐标,并求此时的值;(3)、如图2,点Q为抛物线对称轴与轴的交点,点关于轴的对称点为点D.
(1)、求抛物线的解析式;(2)、如图1,点为直线上方抛物线上任意一点,连、、 , 交直线于点 , 设 , 求当取最大值时点P的坐标,并求此时的值;(3)、如图2,点Q为抛物线对称轴与轴的交点,点关于轴的对称点为点D.①求的周长及的值;
②点M是y轴负半轴上的点,且满足(为大于0的常数),求点M的坐标.