山东省青岛市2021年中考数学真题
试卷更新日期:2022-03-10 类型:中考真卷
一、单选题
-
1. 剪纸是我国古老的民间艺术,下列四个剪纸图案为轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
2. 下列各数为负分数的是( )A、-1 B、 C、0 D、
-
3. 如图所示的几何体,其左视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、
-
4. 2021年3月5 日,李克强总理在政府工作报告中指出,我国脱贫攻坚成果举世瞩目,5575万农村贫困人口实现脱贫.5575万=55750000,用科学记数法将55750000表示为( )A、 B、 C、 D、
-
5. 如图,将线段先绕原点按逆时针方向旋转 , 再向下平移4个单位,得到线段 , 则点的对应点的坐标是( )
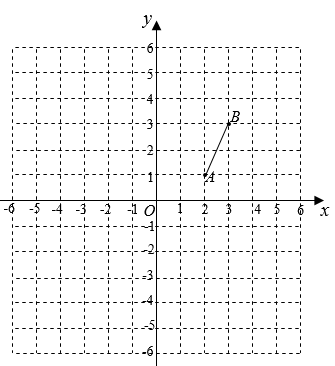 A、 B、 C、 D、
A、 B、 C、 D、 -
6. 如图,是的直径,点 , 在上,点是的中点,过点画的切线,交的延长线于点 , 连接 . 若 , 则的度数为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
7. 如图,在四边形纸片中, , , . 将纸片折叠,使点落在边上的点处,折痕为 . 若 , 则的长为( )
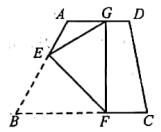 A、5 B、 C、 D、
A、5 B、 C、 D、 -
8. 已知反比例函数的图象如图所示,则一次函数和二次函数在同一直角坐标系中的图象可能是( )
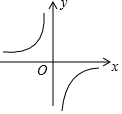 A、
A、 B、
B、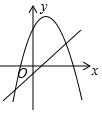 C、
C、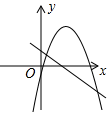 D、
D、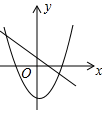
二、填空题
-
9. 计算: .
-
10. 在一个不透明的袋中装有若干个红球和4个黑球,每个球除颜色外完全相同.摇匀后从中摸出一个球,记下颜色后再放回袋中.不断重复这一过程,共摸球100次.其中有40次摸到黑球,估计袋中红球的个数是 .
-
11. 列车从甲地驶往乙地.行完全程所需的时间与行驶的平均速度之间的反比例函数关系如图所示.若列车要在内到达,则速度至少需要提高到 .

-
12. 已知甲、乙两队员射击的成绩如图,设甲、乙两队员射击成绩的方差分别为、 , 则 . (填“”、“”、“”)

-
13. 如图,正方形内接于 , , 分别与相切于点和点 , 的延长线与的延长线交于点 . 已知 , 则图中阴影部分的面积为 .
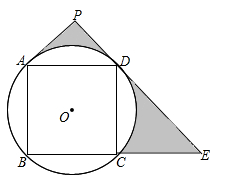
-
14. 已知正方形的边长为3,为上一点,连接并延长,交的延长线于点 , 过点作 , 交于点 , 交于点 , 为的中点,为上一动点,分别连接 , . 若 , 则的最小值为 .
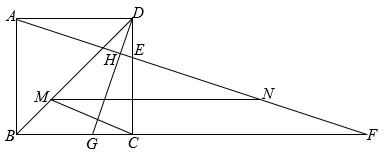
三、解答题
-
15. 已知:及其一边上的两点 , .
求作: , 使 , 且点在内部, .
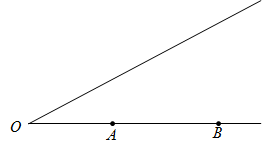
-
16.(1)、计算:;(2)、解不等式组: , 并写出它的整数解.
-
17. 为践行青岛市中小学生“十个一”行动,某校举行文艺表演,小静和小丽想合唱一首歌.小静想唱《红旗飘飘》,而小丽想唱《大海啊,故乡》.她们想通过做游戏的方式来决定合唱哪一首歌,于是一起设计了一个游戏:下面是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形.同时转动两个转盘,若两个指针指向的数字之积小于4,则合唱《大海啊,故乡》,否则合唱《红旗飘飘》;若指针刚好落在分割线上,则需要重新转动转盘.请用列表或画树状图的方法说明这个游戏是否公平.

-
18. 某校数学社团开展“探索生活中的数学”研学活动,准备测量一栋大楼的高度.如图所示,其中观景平台斜坡的长是20米,坡角为 , 斜坡底部与大楼底端的距离为74米,与地面垂直的路灯的高度是3米,从楼顶测得路灯项端处的俯角是 . 试求大楼的高度.
(参考数据: , , , , , )

-
19. 在中国共产党成立一百周年之际,某校举行了以“童心向党”为主题的知识竞赛活动.发现该校全体学生的竞赛成绩(百分制)均不低于60分,现从中随机抽取名学生的竞赛成绩进行整理和分析(成绩得分用表示,共分成四组),并绘制成如下的竞赛成绩分组统计表和扇形统计图.其中“”这组的数据如下:
90,92,93,95,95,96,96,96,97,100.
竞赛成绩分组统计表
组别
竞赛成绩分组
频数
平均分
1
8
65
2
75
3
88
4
10
95
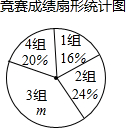
请根据以上信息,解答下列问题:
(1)、;(2)、“”这组数据的众数是分;(3)、随机抽取的这名学生竞赛成绩的平均分是分;(4)、若学生竞赛成绩达到96分以上(含96分)获奖,请你估计全校1200名学生中获奖的人数. -
20. 某超市经销甲、乙两种品牌的洗衣液,进货时发现,甲品牌洗衣液每瓶的进价比乙品牌高6元,用1800元购进甲品牌洗衣液的数量是用1800元购进乙品牌洗衣液数量的 . 销售时,甲品牌洗衣液的售价为36元/瓶,乙品牌洗衣液的售价为28元/瓶.(1)、求两种品牌洗衣液的进价;(2)、若超市需要购进甲、乙两种品牌的洗衣液共120瓶,且购进两种洗衣液的总成本不超过3120元,超市应购进甲、乙两种品牌洗衣液各多少瓶,才能在两种洗衣液完全售出后所获利润最大?最大利润是多少元?
-
21. 如图,在中,为边的中点,连接并延长,交的延长线于点 , 延长至点 , 使 , 分别连接 , , .
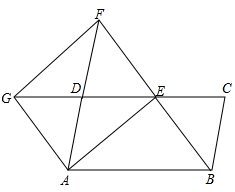 (1)、求证:;(2)、当平分时,四边形是什么特殊四边形?请说明理由.
(1)、求证:;(2)、当平分时,四边形是什么特殊四边形?请说明理由. -
22. 科研人员为了研究弹射器的某项性能,利用无人机测量小钢球竖直向上运动的相关数据.无人机上升到离地面30米处开始保持匀速竖直上升,此时,在地面用弹射器(高度不计)竖直向上弹射一个小钢球(忽路空气阻力),在1秒时,它们距离地面都是35米,在6秒时,它们距离地面的高度也相同.其中无人机离地面高度(米)与小钢球运动时间(秒)之间的函数关系如图所示;小钢球离地面高度(米)与它的运动时间(秒)之间的函数关系如图中抛物线所示.
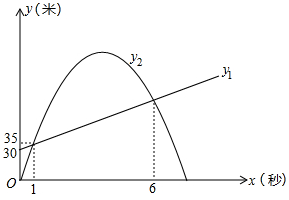 (1)、直接写出与之间的函数关系式;(2)、求出与之间的函数关系式;(3)、小钢球弹射1秒后直至落地时,小钢球和无人机的高度差最大是多少米?
(1)、直接写出与之间的函数关系式;(2)、求出与之间的函数关系式;(3)、小钢球弹射1秒后直至落地时,小钢球和无人机的高度差最大是多少米? -
23. 问题提出:
最长边长为128的整数边三角形有多少个?(整数边三角形是指三边长度都是整数的三角形.)
问题探究:
为了探究规律,我们先从最简单的情形入手,从中找到解决问题的方法,最后得出一般性的结论.
①如表①,最长边长为1的整数边三角形,显然,最短边长是1,第三边长也是1.按照(最长边长,最短边长,第三边长)的形式记为 , 有1个,所以总共有个整数边三角形.
表①
最长边长
最短边长
(最长边长,最短边长,第三边长)
整数边三角形个数
计算方法
算式
1
1
1
1个1
②如表②,最长边长为2的整数边三角形,最短边长是1或2.根据三角形任意两边之和大于第三边,当最短边长为1时,第三边长只能是2,记为 , 有1个;当最短边长为2时,显然第三边长也是2,记为 , 有1个,所以总共有个整数边三角形.
表②
最长边长
最短边长
(最长边长,最短边长,第三边长)
整数边三角形个数
计算方法
算式
2
1
1
2个1
2
1
③下面在表③中总结最长边长为3的整数边三角形个数情况:
表③
最长边长
最短边长
(最长边长,最短边长,第三边长)
整数边三角形个数
计算方法
算式
3
1
1
2个2
2
,
2
3
1
④下面在表④中总结最长边长为4的整数边三角形个数情况:
表④
最长边长
最短边长
(最长边长,最短边长,第三边长)
整数边三角形个数
计算方法
算式
4
1
1
3个2
2
,
2
3
,
2
4
1
(1)、请在表⑤中总结最长边长为5的整数边三角形个数情况并填空:表⑤
最长边长
最短边长
(最长边长,最短边长,第三边长)
整数边三角形个数
计算方法
算式
5
1
1
.......
.......
2
,
2
3
......
......
4
,
2
5
1
(2)、问题解决:最长边长为6的整数边三角形有个.
(3)、在整数边三角形中,设最长边长为 , 总结上述探究过程,当为奇数或为偶数时,整数边三角形个数的规律一样吗?请写出最长边长为的整数边三角形的个数.(4)、最长边长为128的整数边三角形有个.(5)、拓展延伸:在直三棱柱中,若所有棱长均为整数,则最长棱长为9的直三棱柱有个.
-
24. 已知:如图,在矩形和等腰中, , , . 点从点出发,沿方向匀速运动.速度为;同时,点从点出发,沿方向匀速运动,速度为 . 过点作 , 交于点 , 交于点 , 过点作 , 交于点 . 分别连接 , , 设运动时间为 .
解答下列问题:
 (1)、当时,求的值;(2)、设五边形的面积为 , 求与之间的函数关系式;(3)、当时,求的值;(4)、若与相交于点 , 分别连接和 . 在运动过程中,是否存在某一时刻 , 使?若存在,求出的值;若不存在,请说明理由.
(1)、当时,求的值;(2)、设五边形的面积为 , 求与之间的函数关系式;(3)、当时,求的值;(4)、若与相交于点 , 分别连接和 . 在运动过程中,是否存在某一时刻 , 使?若存在,求出的值;若不存在,请说明理由.
