贵州省黔西南布依族苗族自治州2021-2022学年七年级上学期期末数学试卷

试卷更新日期：2022-03-10 类型：期末考试

进入出卷网下载

一、单选题

1. $- | 2021 | =$ （）

A、2021 B、-2021 C、1 D、0

查看试题解析
2. 2021年黔西南州经济运行呈现稳中向好的良好态势.全州上半年生产总值683.28亿元，比上年同期增长，将数据683.28亿用科学记数法表示为（）

A、 $6.8328 \times 10^{10}$ B、 $6.8328 \times 10^{8}$ C、 $0.68328 \times 10^{11}$ D、 $6.8328 \times 10^{4}$

查看试题解析
3. 如图，从A地到B地有三条路线，由上至下依次记为路线a、b、c，则从A地到B地的最短路线是c，其中蕴含的数学道理是（）

A、两点确定一条直线 B、两点之间，线段最短 C、经过一点有无数条直线 D、直线比曲线短

查看试题解析
4. 将方程 $\frac{x}{2} - \frac{x + 1}{4} = 1$ 去分母，下列变形正确的是（）

A、 $2 x - x + 1 = 1$ B、 $2 x - (x + 1) = 1$ C、 $2 x - x + 1 = 4$ D、 $2 x - (x + 1) = 4$

查看试题解析
5. 下列说法正确的是（）

A、 $- 3 a b^{2}$ 的系数是 $- 3 a$ B、4a³b的次数是3 C、 $2 a + b - 1$ 的各项分别是 $2 a ， b ， - 1$ D、多项式 $x^{2} - x + 1$ 是三次三项式

查看试题解析
6. 如图，赵老师在点O处观测到小明站位点A位于北偏西54°30′的方向，同时观测到小刚站位点B在南偏东15°20′的方向，那么 $∠ AOB$ 的大小是（）

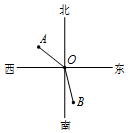A、69°50′ B、110°10′ C、140°50′ D、159°50′

查看试题解析
7. 若 $(3 - m) x^{| m | - 2} - 8 = 0$ 是关于x的一元一次方程，则m的值为（）

A、-3 B、3 C、±3 D、1

查看试题解析
8. 当 $x = 1$ 时，多项式 $a x^{5} + b x^{3} + 4$ 的值为5，则当 $x = - 1$ 时，该多项式的值为（）

A、-5 B、5 C、-3 D、3

查看试题解析
9. 从如图所示的7个小正方形中剪去一个小正方形，使剩余的6个小正方形折叠后能围成一个正方体，则应剪去的小正方形上的字是（）

A、美或贵 B、丽或贵 C、欢或您 D、美或丽或迎

查看试题解析
10. 已知有理数a，b，c在数轴上的对应点的位置如图所示，则下列结论不正确的是（）

A、 $c < a < b$ B、 $a b c < 0$ C、 $a + b < 0$ D、 $| c - b | > | a - b |$

查看试题解析
11. 小亮和家人计划元旦节报团去贞丰县城境内的“圣母峰”游玩，由于节假日旅游旺季，酒店房源紧张，只有混合民宿（一人一个床位）可以选择：若每间房住4人，则有8人无法入住；若每间房住5人，则有一间房空了3个床位.设小亮所在旅游团共有x人，则可列方程为（）

A、 $\frac{x - 8}{4} = \frac{x + 3}{5}$ B、 $\frac{x + 8}{5} = \frac{x - 3}{4}$ C、 $\frac{x}{4} - 8 = \frac{x}{5} + 3$ D、 $4 x + 8 = 5 x - 3$

查看试题解析
12. 如图，数轴上的点 $O$ 和点 $A$ 分别表示0和10，点 $P$ 是线段 $O A$ 上一动点.点 $P$ 沿 $O \to A \to O$ 以每秒2个单位的速度往返运动1次， $B$ 是线段 $O A$ 的中点，设点 $P$ 运动时间为 $t$ 秒（ $t$ 不超过10秒）.若点 $P$ 在运动过程中，当 $P B = 2$ 时，则运动时间 $t$ 的值为（）

A、 $\frac{3}{2}$ 秒或 $\frac{7}{2}$ 秒 B、 $\frac{3}{2}$ 秒或 $\frac{7}{2}$ 秒或 $\frac{13}{2}$ 或 $\frac{17}{2}$ 秒 C、3秒或7秒 D、3秒或 $\frac{13}{2}$ 或7秒或 $\frac{17}{2}$ 秒

查看试题解析

二、填空题

13. 如果把顺时针旋转 $40 °$ 记作 $+ 40 °$ ，那么逆时针旋转 $54 °$ 应记作．

查看试题解析
14. 如图，已知线段AB＝16 cm，M是AB的中点，P是线段MB上一点，N为PB的中点，NB＝3 cm，则线段MP＝cm.

查看试题解析
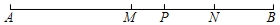15. 对于有理数，定义运算如下： $a * b = \frac{a b}{a + b}$ ，则 $3 * (- 4 * 5) =$ ．

查看试题解析
16. 观察下表，从左向右依次在每个小格子中填入一个有理数，使得其中任意四个相邻小格子中所填数之和都等于15.已知第3个数为7，第5个数为 $a - 1$ ，第8个数为2，第10个数为 $3 - 2 a$ ，则第2022个数为.

7

$a - 1$

2

$3 - 2 a$

$\dots$

查看试题解析

三、解答题

17. 计算：

(1)、 $\frac{1}{8} + (- \frac{3}{8}) - (- \frac{1}{2}) + (- \frac{3}{4})$ ；

(2)、 $(- 3) \times (- 4) + 16 \div {(- 2)}^{3} \times {(- 1)}^{2022} - | - 5 |$ .

查看试题解析
18. 解方程：

(1)、5x﹣4＝2（2x﹣3）

(2)、 $\frac{x - 3}{2}$ ﹣ $\frac{4 x + 1}{5}$ ＝1

查看试题解析
19. 先化简，再求值： $2 (a^{2} - a b) - 3 (2 a^{2} - 3 a b) + 2 [a^{2} - (2 a^{2} - a b)] - 1$ ，其中a，b满足 $2 m^{3 a} n$ 和 $- 2 m^{6} n^{b + 2}$ 是同类项.

查看试题解析
20. 如图，点O在直线 $A B$ 上， $∠ C O D = 60 ° ， ∠ A O E = 2 ∠ D O E$ .

(1)、若 $∠ B O D = 60 °$ ，求 $∠ C O E$ 的度数；

(2)、试猜想 $∠ B O D$ 和 $∠ C O E$ 的数量关系，并说明理由.

查看试题解析
21.

(1)、已知有理数a，b，c在数轴上的对应点的位置如图所示，化简： $| a + b | - | c - b | + | b - a |$ ；

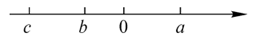(2)、若x的相反数是-2，y没有倒数， $z^{2} = 4$ ，求 $- x + 2 y + z - (x + y - z)$ 的值.

查看试题解析

22. 某仓库在一周的货品运输中，进出情况如表（进库为正，出库为负，单位：吨）：

星期一	星期二	星期三	星期四	星期五	星期六	星期天	合计
＋26	﹣16	＋42	﹣30		﹣25	﹣9	＋6

表中星期五的进出数被墨水涂污了.

(1)、请你算出星期五的进出数；

(2)、如果进出的装卸费都是每吨10元，那么这一周要付多少元装卸费？

查看试题解析

23. 已知点 $C$ 在线段 $A B$ 上， $A C = 2 B C$ ，点 $D$ 、 $E$ 在直线 $A B$ 上，点 $D$ 在点 $E$ 的左侧.若 $A B = 18$ ， $D E = 8$ ，线段 $D E$ 在线段 $A B$ 上移动.

(1)、如图1，当 $E$ 为 $B C$ 中点时，求 $A D$ 的长；

(2)、点 $F$ （异于 $A$ ， $B$ ， $C$ 点）在线段 $A B$ 上， $A F = 3 A D$ ， $C E + E F = 3$ ，求 $A D$ 的长.

查看试题解析
24. 小商品批发市场内，某商品的价格按如下优惠：购买不超过300件时，每件3元；超过300件但不超过500件时，每件2.5元；超过500件时，每件2元.某客户欲采购这种小商品700件.

(1)、现有两种购买方案：①分两次购买，第一次购买200件，第二次购买500件；②一次性购买700件.按哪种方案购买更省钱？说明理由.

(2)、若该客户分两次购买该商品共700件（第一次购买不超过300件），共付费1860元，求第一次和第二次分别购买该商品多少件.

查看试题解析
25. 已知数轴上两点A、B对应的数分别为﹣1、3，点P为数轴上一动点，其对应的数为x.

(1)、如果点P到点A、点B的距离相等，直接写出x的值；

(2)、当点P以每秒3个单位长的速度从数轴的原点出发，几秒后可使PB＝3AB？

(3)、利用数轴，根据绝对值的几何意义，找出满足|x+1|+|x﹣3|＝6的所有x的值.

查看试题解析