2022年浙江省中考专项复习5 二次函数的应用
试卷更新日期:2022-03-09 类型:一轮复习
一、单选题
-
1. 抛物线 与y轴交点的坐标是( )A、(0,3) B、(3,0) C、(1,0) D、(0,1)2. 关于x的函数与x轴有交点,则a的取值范围是( )A、 B、 C、且 D、且3. 商店销售一种进价为50元/件的商品,售价为60元/件,每星期可卖出200件,若每件商品的售价上涨1元,则每星期就会少卖10件.每件商品的售价上涨x元(x正整数),每星期销售的利润为y元,则y与x的函数关系式为( )A、y=10(200﹣10x) B、y=200(10+x) C、y=10(200﹣10x)2 D、y=(10+x)(200﹣10x)4. 如图,一个矩形的长比宽多3cm,矩形的面积是Scm2 . 设矩形的宽为xcm,当x在一定范围内变化时,S随x的变化而变化,则S与x满足的函数关系是( )
 A、S=4x+6 B、S=4x-6 C、S=x2+3x D、S=x2-3x5. 在平面直角坐标系中,二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论正确的( )
A、S=4x+6 B、S=4x-6 C、S=x2+3x D、S=x2-3x5. 在平面直角坐标系中,二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论正确的( )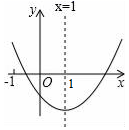 A、ac>0 B、b2﹣4ac<0 C、4a+2b+c<0 D、b=2a6. 小颖用计算器探索方程ax2+bx+c=0的根,作出如图所示的图象,并求得一个近似根x=﹣3.4,则方程的另一个近似根(精确到0.1)为( )
A、ac>0 B、b2﹣4ac<0 C、4a+2b+c<0 D、b=2a6. 小颖用计算器探索方程ax2+bx+c=0的根,作出如图所示的图象,并求得一个近似根x=﹣3.4,则方程的另一个近似根(精确到0.1)为( ) A、4.4 B、3.4 C、2.4 D、1.47. 我们定义两个不相交的函数图象在竖直方向上的最短距离为这两个函数的“和谐值”.抛物线 与直线 的“和谐值”为( )A、3 B、 C、 D、28. 一位运动员在离篮筐水平距离4m处起跳投篮,球运行路线可看作抛物线,当球离开运动员的水平距离为1m时,它与篮筐同高,球运行中的最大高度为3.5m,最后准确落入篮筐,已知篮筐到地面的距离为3.05m,该运动员投篮出手点距离地面的高度为( )
A、4.4 B、3.4 C、2.4 D、1.47. 我们定义两个不相交的函数图象在竖直方向上的最短距离为这两个函数的“和谐值”.抛物线 与直线 的“和谐值”为( )A、3 B、 C、 D、28. 一位运动员在离篮筐水平距离4m处起跳投篮,球运行路线可看作抛物线,当球离开运动员的水平距离为1m时,它与篮筐同高,球运行中的最大高度为3.5m,最后准确落入篮筐,已知篮筐到地面的距离为3.05m,该运动员投篮出手点距离地面的高度为( ) A、1.5m B、2m C、2.25m D、2.5m9. 如图,已知顶点为(﹣3,﹣6)的抛物线y=ax2+bx+c经过点(﹣1,﹣4),则下列结论:①abc>0;②4a﹣2b+c<0;③b2>4ac;④ax2+bx+c≥﹣6;⑤若点M(﹣2,m)与点N(﹣5,n)为抛物线上两点,则m>n;⑥关于x的一元二次方程ax2+bx+c=﹣4的两根为﹣5和﹣1.其中正确结论有( )
A、1.5m B、2m C、2.25m D、2.5m9. 如图,已知顶点为(﹣3,﹣6)的抛物线y=ax2+bx+c经过点(﹣1,﹣4),则下列结论:①abc>0;②4a﹣2b+c<0;③b2>4ac;④ax2+bx+c≥﹣6;⑤若点M(﹣2,m)与点N(﹣5,n)为抛物线上两点,则m>n;⑥关于x的一元二次方程ax2+bx+c=﹣4的两根为﹣5和﹣1.其中正确结论有( )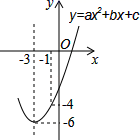 A、5 B、4 C、3 D、210. 如图,已知二次函数y=﹣ (x+1)(x﹣4)的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,P为该二次函数在第一象限内的一点,连接AP,交BC于点K,则 的最小值为( )
A、5 B、4 C、3 D、210. 如图,已知二次函数y=﹣ (x+1)(x﹣4)的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,P为该二次函数在第一象限内的一点,连接AP,交BC于点K,则 的最小值为( )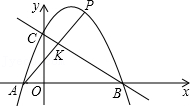 A、 B、2 C、 D、
A、 B、2 C、 D、二、填空题
-
11. 抛物线 与 的一个交点坐标是 ,则另一个交点坐标是 .12. 在关于的 二次函数中,自变量 可以取任意实数,下表是自变量 与函数 的几组对应值:
…
1
2
3
4
5
6
7
8
…
…
-1.78
-3.70
-4.42
-3.91
-2.20
4.88
10.27
…
根据以上信息,关于 的一元二次方程 的两个实数根中,其中的一个实数根约等于(结果保留小数点后一位).
13. 某果园有100棵橘子树,平均每一棵树结600个橘子.根据经验估计,每多种一棵树,平均每棵树就会少结5个橘子.设果园增种x棵橘子树,果园橘子总个数为y个,则果园里增种棵橘子树,橘子总个数最多.14. 如图,已知抛物线 与 轴交于 、 两点,与 轴交于 点, 的半径为2. 为 上一动点, 为 的中点,则 的最小值为 , 的最大值为 . 15. 为响应“足球进校园”的号召,我县教体局在今年 11 月份组织了“县长杯”校园足球比赛.在某场比赛中,一个球被从地面向上踢出,它距地面的高度 h(m)可用公式 h=﹣5t2+v0t 表示,其中 t(s)表示足球被踢出后经过的时间,v0(m/s)是足球被踢出时的速度,如果足球的最大高度到 20m,那么足球被踢出时的速度应达到m/s.16. 如图,垂直于x轴的直线AB分别与抛物线C1:y=x2(x≥0)和抛物线C2:y=(x≥0)交于A,B两点,过点A作CD∥x轴分别与y轴和抛物线C2交于点C、D,过点B作EF∥x轴分别与y轴和抛物线C1交于点E、F,则 的值为.
15. 为响应“足球进校园”的号召,我县教体局在今年 11 月份组织了“县长杯”校园足球比赛.在某场比赛中,一个球被从地面向上踢出,它距地面的高度 h(m)可用公式 h=﹣5t2+v0t 表示,其中 t(s)表示足球被踢出后经过的时间,v0(m/s)是足球被踢出时的速度,如果足球的最大高度到 20m,那么足球被踢出时的速度应达到m/s.16. 如图,垂直于x轴的直线AB分别与抛物线C1:y=x2(x≥0)和抛物线C2:y=(x≥0)交于A,B两点,过点A作CD∥x轴分别与y轴和抛物线C2交于点C、D,过点B作EF∥x轴分别与y轴和抛物线C1交于点E、F,则 的值为. 17. 如图,矩形 中, ,点 为边 上一动点(不与 重合)、以 为边向外作矩形 ,且 ,连接 点 是线段BF的中点.连接 ,则 的最小值为.
17. 如图,矩形 中, ,点 为边 上一动点(不与 重合)、以 为边向外作矩形 ,且 ,连接 点 是线段BF的中点.连接 ,则 的最小值为.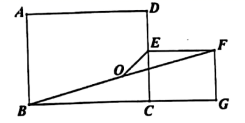
三、综合题
-
18. 一名男生推铅球,铅球的行进高度
 (单位:
(单位: 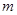 )与水平距离
)与水平距离 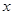 (单位:
(单位: 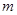 )之间的关系为 ,铅球行进路线如图.
)之间的关系为 ,铅球行进路线如图.
 (1)、求出手点离地面的高度.(2)、求铅球推出的水平距离.(3)、通过计算说明铅球的行进高度能否达到4
(1)、求出手点离地面的高度.(2)、求铅球推出的水平距离.(3)、通过计算说明铅球的行进高度能否达到4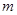 . 19. 生态水果是指在保护、改善农业生态环境的前提下,遵循生态学、生态经济学规律,运用现代科学技术,营养的、健康的水果.青岛市扶贫工作小组对李沧、胶州、即墨等多地果农进行精准投资建设,帮助果农将一种有机生态水果拓宽了市场,今年这种水果的产量增加了1000千克,每千克的平均批发价比去年降低了 . 批发销售总额比去年增加了20%(1)、已知去年这种水果批发销售总额为10万元,求这种水果今年每千克的平均批发价是多少元?(2)、今年某水果店从果农处直接批发,专营这种水果.调查发现,若每千克的平均销售价为41元,则每天可售出300千克;若每千克的平均销售价每降低3元,每天可多卖出180千克.设水果店一天的利润为w元,当每千克的平均销售价为多少元时该水果店一天的利润最大(利润计算时,其它费用忽略不计,并且售价为整数)20. 如图
. 19. 生态水果是指在保护、改善农业生态环境的前提下,遵循生态学、生态经济学规律,运用现代科学技术,营养的、健康的水果.青岛市扶贫工作小组对李沧、胶州、即墨等多地果农进行精准投资建设,帮助果农将一种有机生态水果拓宽了市场,今年这种水果的产量增加了1000千克,每千克的平均批发价比去年降低了 . 批发销售总额比去年增加了20%(1)、已知去年这种水果批发销售总额为10万元,求这种水果今年每千克的平均批发价是多少元?(2)、今年某水果店从果农处直接批发,专营这种水果.调查发现,若每千克的平均销售价为41元,则每天可售出300千克;若每千克的平均销售价每降低3元,每天可多卖出180千克.设水果店一天的利润为w元,当每千克的平均销售价为多少元时该水果店一天的利润最大(利润计算时,其它费用忽略不计,并且售价为整数)20. 如图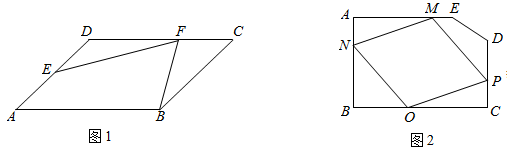 (1)、问题提出
(1)、问题提出如图1,在 中, , , ,E是 的中点,点F在 上且 求四边形 的面积.(结果保留根号)
(2)、问题解决某市进行河滩治理,优化美化人居生态环境.如图2所示,现规划在河畔的一处滩地上建一个五边形河畔公园 按设计要求,要在五边形河畔公园 内挖一个四边形人工湖 ,使点O、P、M、N分别在边 、 、 、 上,且满足 , .已知五边形 中, , , , , .满足人工湖周边各功能场所及绿化用地需要,想让人工湖面积尽可能小.请问,是否存在符合设计要求的面积最小的四边形人工湖 ?若存在,求四边形 面积的最小值及这时点 到点 的距离;若不存在,请说明理由.
21. 阅读下列材料,解决材料后的问题:材料一:对于实数x、y,我们将x与y的“友好数”用f(x,y)表示,定义为: ,例如17与16的友好数为 .
材料二:对于实数 ,用 表示不超过实数 的最大整数,即满足条件 ≤ < ,例如:
, , ,……
(1)、由材料一知: 与1的“友好数”可以用 表示,已知 ,请求出 的值;(2)、已知 ,请求出实数a的取值范围;(3)、已知实数 满足条件 ,且 ,请求 的最小值.22. 如图①,在 中, 于点 , , , 点 是 上一动点(不与点 , 重合),在 内作矩形 ,点 在 上,点 , 在 上,设 ,连接 .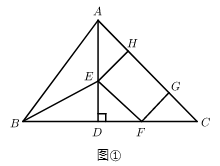
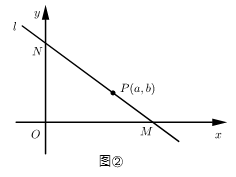 (1)、当矩形 是正方形时,直接写出 的长;(2)、设 的面积为 ,矩形 的面积为 ,令 ,求 关于 的函数解析式(不要求写出自变量 的取值范围);(3)、如图②,点 是(2)中得到的函数图象上的任意一点,过点 的直线 分别与 轴正半轴, 轴正半轴交于 , 两点,求 面积的最小值,并说明理由.
(1)、当矩形 是正方形时,直接写出 的长;(2)、设 的面积为 ,矩形 的面积为 ,令 ,求 关于 的函数解析式(不要求写出自变量 的取值范围);(3)、如图②,点 是(2)中得到的函数图象上的任意一点,过点 的直线 分别与 轴正半轴, 轴正半轴交于 , 两点,求 面积的最小值,并说明理由.