2022年浙江省中考专项复习4 二次函数图象与性质
试卷更新日期:2022-03-09 类型:一轮复习
一、单选题
-
1. 下列函数中,属于二次函数的是( )A、 B、 C、 D、2. 下列具有二次函数关系的是( )A、正方形的周长y与边长x B、速度一定时,路程s与时间t C、三角形的高一定时,面积y与底边长x D、正方形的面积y与边长x3. 二次函数y=x2+4x-5的图象的对称轴为( )A、x=4 B、x=-4 C、x=2 D、x=-24. 将二次函数 的图象向左平移1个单位长度, 再向上平移2个单位后, 所得图象 的函数解析式是( )A、 B、 C、 D、5. 如图,某农场拟建一间矩形奶牛饲养室,打算一边利用房屋现有的墙(墙足够长),其余三边除大门外用栅栏围成,栅栏总长度为50m,门宽为2m.若饲养室长为xm,占地面积为y ,则y关于x的函数表达式为( )
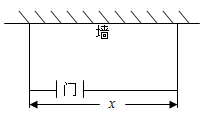 A、y=﹣ x2+26x(2≤x<52) B、y=﹣ x2+50x(2≤x<52) C、y=﹣x2+52x(2≤x<52) D、y=﹣ x2+27x﹣52(2≤x<52)6. 在同一平面直角坐标系中,二次函数y=ax2与一次函数y=bx+c的图象如图所示,则二次函数y=ax2-bx+c的图象可能是( )
A、y=﹣ x2+26x(2≤x<52) B、y=﹣ x2+50x(2≤x<52) C、y=﹣x2+52x(2≤x<52) D、y=﹣ x2+27x﹣52(2≤x<52)6. 在同一平面直角坐标系中,二次函数y=ax2与一次函数y=bx+c的图象如图所示,则二次函数y=ax2-bx+c的图象可能是( ) A、
A、 B、
B、 C、
C、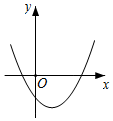 D、
D、 7. “如果二次函数 的图像与 轴有两个交点,那么一元二次方程 有两个不相等的实数根.”请根据这句话的理解,解决以下问题;若 、 是关于 的方程 的两根,且 ,则 , , , 的大小关关系是( )A、 B、 C、 D、8. 如图,过点C(1,2)分别作x轴、y轴的平行线,交直线y=-x+6于A,B两点,若反比例函数 (x>0)的图象与△ABC有公共点,则k的取值范围是( )
7. “如果二次函数 的图像与 轴有两个交点,那么一元二次方程 有两个不相等的实数根.”请根据这句话的理解,解决以下问题;若 、 是关于 的方程 的两根,且 ,则 , , , 的大小关关系是( )A、 B、 C、 D、8. 如图,过点C(1,2)分别作x轴、y轴的平行线,交直线y=-x+6于A,B两点,若反比例函数 (x>0)的图象与△ABC有公共点,则k的取值范围是( ) A、2≤k≤8 B、2≤k≤9 C、2≤k≤5 D、5≤k≤89. 如图,一段抛物线:y=-x(x-3)(0≤x≤3),记为C1 , 它与x轴交于点O , A1;将C1绕点A1旋转180°得C2 , 交x轴于点A2;将C2绕点A2旋转180°得C3 , 交x轴于点A3;…如此进行下去,直至得C5 . 若P(14,m)在第5段抛物线C5上,则m值为( )
A、2≤k≤8 B、2≤k≤9 C、2≤k≤5 D、5≤k≤89. 如图,一段抛物线:y=-x(x-3)(0≤x≤3),记为C1 , 它与x轴交于点O , A1;将C1绕点A1旋转180°得C2 , 交x轴于点A2;将C2绕点A2旋转180°得C3 , 交x轴于点A3;…如此进行下去,直至得C5 . 若P(14,m)在第5段抛物线C5上,则m值为( ) A、2 B、1.5 C、-2 D、-2.2510. 如图,二次函数 的图象与 轴交于 、 两点,与 轴交于点 ,且 ,则下列结论:① ;② ;③当 时, 随 的增大而增大;④将抛物线在 轴左侧的部分沿过点 且平行于 轴的直线 翻折,抛物线的其余部分保持不变得到一个新图象,当函数 ( 为常数)的图象与新图象有3个公共点时, 的取值范围是 ,其中正确的个数是( )
A、2 B、1.5 C、-2 D、-2.2510. 如图,二次函数 的图象与 轴交于 、 两点,与 轴交于点 ,且 ,则下列结论:① ;② ;③当 时, 随 的增大而增大;④将抛物线在 轴左侧的部分沿过点 且平行于 轴的直线 翻折,抛物线的其余部分保持不变得到一个新图象,当函数 ( 为常数)的图象与新图象有3个公共点时, 的取值范围是 ,其中正确的个数是( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 如果抛物线的顶点在轴上,那么的值是 .12. 将二次函数的图象沿x轴向右平移2个单位长度,得到的函数解析式是.13. 如图,在平面直角坐标系中,抛物线y=﹣(x﹣3)2+m与y=(x+2)2+n的一个交点为A.已知点A的横坐标为1,过点A作x轴的平行线,分别交两条抛物线于点B、C(点B在点A左侧,点C在点A右侧),则的值为 .
 14. 如图,将函数的图象沿y轴向上平移得到一条新函数的图象,其中点 , 平移后的对应点分别为点、.若曲线段AB扫过的面积为12(图中的阴影部分),则新图象的函数表达式是.
14. 如图,将函数的图象沿y轴向上平移得到一条新函数的图象,其中点 , 平移后的对应点分别为点、.若曲线段AB扫过的面积为12(图中的阴影部分),则新图象的函数表达式是. 15. 二次函数的图象如图所示,点位于坐标原点,点 , , , …,在y轴的正半轴上,点 , , , …,在二次函数位于第一象限的图象上, , , …,都是直角顶点在抛物线上的等腰直角三角形,则的斜边长为 .
15. 二次函数的图象如图所示,点位于坐标原点,点 , , , …,在y轴的正半轴上,点 , , , …,在二次函数位于第一象限的图象上, , , …,都是直角顶点在抛物线上的等腰直角三角形,则的斜边长为 . 16. 如图,在平面直角坐标系中,以点C(1,1)为圆心,2为半径作圆,交x轴于A , B两点,点P在 上.请写出经过A、B且以点P为顶点的抛物线解析式 .
16. 如图,在平面直角坐标系中,以点C(1,1)为圆心,2为半径作圆,交x轴于A , B两点,点P在 上.请写出经过A、B且以点P为顶点的抛物线解析式 .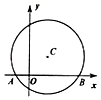 17. 如图,正方形ABCD的边长为2,E为边AD上一动点,连接CE,以CE为边向右侧作正方形CEFG,连接DF,DG,则面积的最小值为 .
17. 如图,正方形ABCD的边长为2,E为边AD上一动点,连接CE,以CE为边向右侧作正方形CEFG,连接DF,DG,则面积的最小值为 .
三、作图题
-
18. 若二次函数 的 与 的部分对应值如下表:
…
-4
-3
-2
-1
0
1
…
…
-5
0
3
4
3
0
…
 (1)、求此二次函数的解析式;(2)、画出此函数图象(不用列表);(3)、结合函数图象,当 时,直接写出 的取值范围.
(1)、求此二次函数的解析式;(2)、画出此函数图象(不用列表);(3)、结合函数图象,当 时,直接写出 的取值范围.四、解答题
-
19. 若点 , , 在抛物线 的图象上,请判断 , , 的大小关系,并说明理由.20. 已知二次函数的图像经过两点(1)、求二次函数的解析式:(2)、将该二次函数的解析式化为的形式,并写出该二次函数图象的开口方向、顶点坐标和对称轴
五、综合题
-
21. 定义: 若抛物线 与地物线 . 同时满足 且 , 则称这两条抛物线是一对 “共轭抛物线".
 (1)、已知抛物线 与 是一对共轭抛物线, 求 的解折式:(2)、如图1,将一副边长为 的正方形七巧板拼成图2的形式, 若以BC中点为原点,直线BC为x轴建立平面直角坐标系,设经过点 的抛物线为 , 经过 的抛物线为 , 请立接写出 的解析式并判断它们是否为一对共轭拋物线.22. 如图,在平面直角坐标系xOy中,抛物线y=ax2+2x+c(a≠0)与x轴交于点A(﹣1,0)和点B,交y轴于点C(0,3),顶点为D.
(1)、已知抛物线 与 是一对共轭抛物线, 求 的解折式:(2)、如图1,将一副边长为 的正方形七巧板拼成图2的形式, 若以BC中点为原点,直线BC为x轴建立平面直角坐标系,设经过点 的抛物线为 , 经过 的抛物线为 , 请立接写出 的解析式并判断它们是否为一对共轭拋物线.22. 如图,在平面直角坐标系xOy中,抛物线y=ax2+2x+c(a≠0)与x轴交于点A(﹣1,0)和点B,交y轴于点C(0,3),顶点为D. (1)、求抛物线解析式;(2)、点E为线段BD上的一个动点,作EF⊥x轴于点F,连接OE,当△OEF面积最大时.求点E的坐标;(3)、G是第四象限内抛物线上一点,过点G作GH⊥x轴于点H,交直线BD于点K、且 , 作直线AG.
(1)、求抛物线解析式;(2)、点E为线段BD上的一个动点,作EF⊥x轴于点F,连接OE,当△OEF面积最大时.求点E的坐标;(3)、G是第四象限内抛物线上一点,过点G作GH⊥x轴于点H,交直线BD于点K、且 , 作直线AG.①点G的坐标是 ;
②P为直线AG上方抛物线上一点,过点P作PQ⊥AG于点Q,取点 , 点N为平面内一点,若四边形MPNQ是菱形,请直接写出菱形的边长.
23. 如图1,在平面直角坐标系 中,抛物线 经过点 ,且与直线 在第二象限交于点A,过点A作 轴,垂足为点 .若P是直线 上方该抛物线上的一个动点,过点P作 轴于点C,交 于点D,连接 , . (1)、求抛物线的解析式;(2)、求 的面积S的最大值;(3)、连接 交 于点E,如图2,线段 与 能否互相平分?若能,请求出点E的坐标;若不能,请说明理由.
(1)、求抛物线的解析式;(2)、求 的面积S的最大值;(3)、连接 交 于点E,如图2,线段 与 能否互相平分?若能,请求出点E的坐标;若不能,请说明理由.
-