2022届中考数学 二轮必刷选择题 全国通用
试卷更新日期:2022-03-08 类型:二轮复习
一、单选题
-
1. 如图,将图1中的菱形纸片沿对角线剪成4个直角三角形,拼成如图2的四边形 (相邻纸片之间不重叠,无缝隙).若四边形 的面积为13,中间空白处的四边形 的面积为1,直角三角形的两条直角边分别为 和 ,则 ( )
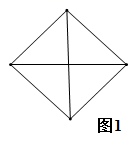
 A、12 B、13 C、24 D、252. 如图,菱形 的对角线 与 相交于点 ,点 在 上,连接 , , , , ,则 ( )
A、12 B、13 C、24 D、252. 如图,菱形 的对角线 与 相交于点 ,点 在 上,连接 , , , , ,则 ( )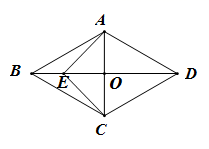 A、4 B、3 C、 D、23. 如图,在平面直角坐标系中, , , , ,将四边形 向左平移 个单位后,点 恰好和原点 重合,则 的值是( )
A、4 B、3 C、 D、23. 如图,在平面直角坐标系中, , , , ,将四边形 向左平移 个单位后,点 恰好和原点 重合,则 的值是( ) A、11.4 B、11.6 C、12.4 D、12.64. 如图,在 中, , , ,且 ,若 ,点 是线段 上的动点,则 的最小值是( )
A、11.4 B、11.6 C、12.4 D、12.64. 如图,在 中, , , ,且 ,若 ,点 是线段 上的动点,则 的最小值是( )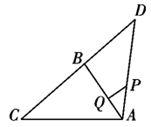 A、 B、 C、 D、5. 如图, 是 的外接圆,CD是 的直径.若 ,弦 ,则 的值为( )
A、 B、 C、 D、5. 如图, 是 的外接圆,CD是 的直径.若 ,弦 ,则 的值为( )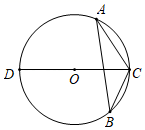 A、 B、 C、 D、6. 对于二次函数 ,有以下结论:①当 时,y随x的增大而增大;②当 时,y有最小值3;③图象与x轴有两个交点;④图象是由抛物线 向左平移6个单位长度,再向上平移3个单位长度得到的.其中结论正确的个数为( )A、1 B、2 C、3 D、47. 如图,在 中, ,点C为边AB上一点,且 .如果函数 的图象经过点B和点C , 那么用下列坐标表示的点,在直线BC上的是( )
A、 B、 C、 D、6. 对于二次函数 ,有以下结论:①当 时,y随x的增大而增大;②当 时,y有最小值3;③图象与x轴有两个交点;④图象是由抛物线 向左平移6个单位长度,再向上平移3个单位长度得到的.其中结论正确的个数为( )A、1 B、2 C、3 D、47. 如图,在 中, ,点C为边AB上一点,且 .如果函数 的图象经过点B和点C , 那么用下列坐标表示的点,在直线BC上的是( ) A、(-2019,674) B、(-2020,675) C、(2021,-669) D、(2022,-670)8. 关于x的一元二次方程 的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、实数根的个数由m的值确定9. 如图,在Rt△ABC中,∠A=30°,∠C=90°,AB=6,点P是线段AC上一动点,点M在线段AB上,当AM= AB时,PB+PM的最小值为( )
A、(-2019,674) B、(-2020,675) C、(2021,-669) D、(2022,-670)8. 关于x的一元二次方程 的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、实数根的个数由m的值确定9. 如图,在Rt△ABC中,∠A=30°,∠C=90°,AB=6,点P是线段AC上一动点,点M在线段AB上,当AM= AB时,PB+PM的最小值为( ) A、3 B、2 C、2 +2 D、3 +310. 关于x,y的方程组 的解为 ,若点P(a,b)总在直线y=x上方,那么k的取值范围是( )A、k>1 B、k>﹣1 C、k<1 D、k<﹣111. 已知圆锥的母线长为3,底面圆半径为1,则圆锥侧面展开图的圆心角为( )A、30° B、60° C、120° D、150°12. 已知二次函数y=ax2+bx+c的自变量x与函数y的部分对应值见表格,则下列结论:①c=2;②b2﹣4ac>0;③方程ax2+bx=0的两根为x1=﹣2,x2=0;④7a+c<0.其中正确的有( )
A、3 B、2 C、2 +2 D、3 +310. 关于x,y的方程组 的解为 ,若点P(a,b)总在直线y=x上方,那么k的取值范围是( )A、k>1 B、k>﹣1 C、k<1 D、k<﹣111. 已知圆锥的母线长为3,底面圆半径为1,则圆锥侧面展开图的圆心角为( )A、30° B、60° C、120° D、150°12. 已知二次函数y=ax2+bx+c的自变量x与函数y的部分对应值见表格,则下列结论:①c=2;②b2﹣4ac>0;③方程ax2+bx=0的两根为x1=﹣2,x2=0;④7a+c<0.其中正确的有( )x
…
﹣3
﹣2
﹣1
1
2
…
y
…
1.875
3
m
1.875
0
…
A、①④ B、②③ C、③④ D、②④13. 如图,矩形AOBC的顶点A、B在坐标轴上,点C的坐标是(﹣10,8),点D在AC上,将 BCD沿BD翻折,点C恰好落在OA边上点E处,则tan∠DBE等于( )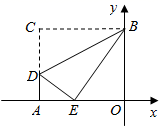 A、 B、 C、 D、14. 两千多年前,古希腊数学家欧多克索斯发现了黄金分割,即:如图,点P是线段AB上一点(AP>BP),若满足 ,则称点P是AB的黄金分割点.黄金分割在日常生活中处处可见,例如:主持人在舞台上主持节目时,站在黄金分割点上,观众看上去感觉最好.若舞台长20米,主持人从舞台一侧进入,设他至少走x米时恰好站在舞台的黄金分割点上,则x满足的方程是( )
A、 B、 C、 D、14. 两千多年前,古希腊数学家欧多克索斯发现了黄金分割,即:如图,点P是线段AB上一点(AP>BP),若满足 ,则称点P是AB的黄金分割点.黄金分割在日常生活中处处可见,例如:主持人在舞台上主持节目时,站在黄金分割点上,观众看上去感觉最好.若舞台长20米,主持人从舞台一侧进入,设他至少走x米时恰好站在舞台的黄金分割点上,则x满足的方程是( ) A、(20﹣x)2=20x B、x2=20(20﹣x) C、x(20﹣x)=202 D、以上都不对15. 如图,△ABC内接于⊙O , AB为⊙O的直径,D为⊙O上一点(位于AB下方),CD交AB于点E , 若∠BDC=45°,BC=6 ,CE=2DE , 则CE的长为( )
A、(20﹣x)2=20x B、x2=20(20﹣x) C、x(20﹣x)=202 D、以上都不对15. 如图,△ABC内接于⊙O , AB为⊙O的直径,D为⊙O上一点(位于AB下方),CD交AB于点E , 若∠BDC=45°,BC=6 ,CE=2DE , 则CE的长为( )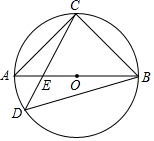 A、2 B、4 C、3 D、416. 如图,已知直线AB和AB上的一点C , 过点C作直线AB的垂线,步骤如下:
A、2 B、4 C、3 D、416. 如图,已知直线AB和AB上的一点C , 过点C作直线AB的垂线,步骤如下:第一步:以点C为圆心,以任意长为半径作弧,交直线AB于点D和点E;
第二步:分别以点D和点E为圆心,以 为半径作弧,两弧交于点F;
第三步:作直线CF , 直线CF即为所求.
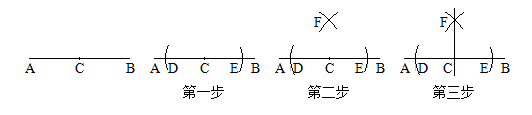
下列关于 的说法正确的是( )
A、 ≥ B、 ≤ C、 D、17. 如图,直线 , 相交于点 . 为这两直线外一点,且 .若点 关于直线 , 的对称点分别是点 , ,则 , 之间的距离可能是( ) A、0 B、5 C、6 D、718. 如图,已知长方形 中, ,圆B的半径为1,圆A与圆B内切,则点 与圆A的位置关系是( )
A、0 B、5 C、6 D、718. 如图,已知长方形 中, ,圆B的半径为1,圆A与圆B内切,则点 与圆A的位置关系是( )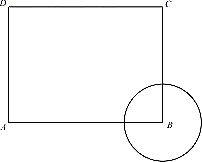 A、点C在圆A外,点D在圆A内 B、点C在圆A外,点D在圆A外 C、点C在圆A上,点D在圆A内 D、点C在圆A内,点D在圆A外19. 已知 和 均是以 为自变量的函数,当 时,函数值分别是 和 ,若存在实数 ,使得 ,则称函数 和 具有性质P。以下函数 和 具有性质P的是( )A、 和 B、 和 C、 和 D、 和20. 如图,在等腰直角 中, , 、 分别为 、 上的点, , 为 上的点,且 , ,则 ( )
A、点C在圆A外,点D在圆A内 B、点C在圆A外,点D在圆A外 C、点C在圆A上,点D在圆A内 D、点C在圆A内,点D在圆A外19. 已知 和 均是以 为自变量的函数,当 时,函数值分别是 和 ,若存在实数 ,使得 ,则称函数 和 具有性质P。以下函数 和 具有性质P的是( )A、 和 B、 和 C、 和 D、 和20. 如图,在等腰直角 中, , 、 分别为 、 上的点, , 为 上的点,且 , ,则 ( )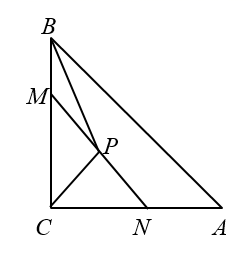 A、 B、 C、 D、21. 如图,在边长为4的正方形ABCD中,点E,F分别在CD,AC上, , ,则AF的长是( )
A、 B、 C、 D、21. 如图,在边长为4的正方形ABCD中,点E,F分别在CD,AC上, , ,则AF的长是( )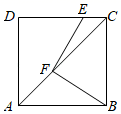 A、 B、 C、 D、22. 甲、乙、丙、丁四名射击运动员进行射击测试,每人10次射击成绩的平均数 (单位:环)及方差 (单位:环 )如下表所示:
A、 B、 C、 D、22. 甲、乙、丙、丁四名射击运动员进行射击测试,每人10次射击成绩的平均数 (单位:环)及方差 (单位:环 )如下表所示:甲
乙
丙
丁
9
8
9
9
1.6
0.8
3
0.8
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应选择( )
A、甲 B、乙 C、丙 D、丁23. 如图,在 中, 于点D, .若E,F分别为 , 的中点,则 的长为( )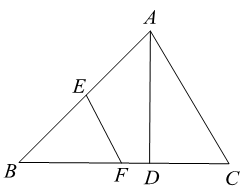 A、 B、 C、1 D、24. 如图,菱形ABCD中, ,点P从点B出发,沿折线 方向移动,移动到点D停止.在 形状的变化过程中,依次出现的特殊三角形是( )
A、 B、 C、1 D、24. 如图,菱形ABCD中, ,点P从点B出发,沿折线 方向移动,移动到点D停止.在 形状的变化过程中,依次出现的特殊三角形是( )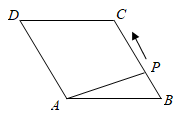 A、直角三角形→等边三角形→等腰三角形→直角三角形 B、直角三角形→等腰三角形→直角三角形→等边三角形 C、直角三角形→等边三角形→直角三角形→等腰三角形 D、等腰三角形→等边三角形→直角三角形→等腰三角形25. 如图,在 中, ,以该三角形的三条边为边向形外作正方形,正方形的顶点 都在同一个圆上.记该圆面积为 , 面积为 ,则 的值是( )
A、直角三角形→等边三角形→等腰三角形→直角三角形 B、直角三角形→等腰三角形→直角三角形→等边三角形 C、直角三角形→等边三角形→直角三角形→等腰三角形 D、等腰三角形→等边三角形→直角三角形→等腰三角形25. 如图,在 中, ,以该三角形的三条边为边向形外作正方形,正方形的顶点 都在同一个圆上.记该圆面积为 , 面积为 ,则 的值是( ) A、 B、 C、 D、26. 图1是第七届国际数学教育大会(ICME)的会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图2所示的四边形 .若 . ,则 的值为( )
A、 B、 C、 D、26. 图1是第七届国际数学教育大会(ICME)的会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图2所示的四边形 .若 . ,则 的值为( ) A、 B、 C、 D、27. 如图,点 , 在反比例函数 ( , )的图象上, 轴于点 , 轴于点 , 轴于点 ,连结 .若 , , ,则 的值为( )
A、 B、 C、 D、27. 如图,点 , 在反比例函数 ( , )的图象上, 轴于点 , 轴于点 , 轴于点 ,连结 .若 , , ,则 的值为( )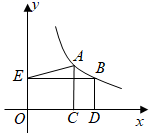 A、2 B、 C、 D、28. 将一张三角形纸片按如图步骤①至④折叠两次得图⑤,然后剪出图⑤中的阴影部分,则阴影部分展开铺平后的图形是( )
A、2 B、 C、 D、28. 将一张三角形纸片按如图步骤①至④折叠两次得图⑤,然后剪出图⑤中的阴影部分,则阴影部分展开铺平后的图形是( )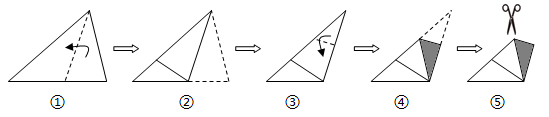 A、等腰三角形 B、直角三角形 C、矩形 D、菱形29. 5月1日至7日,我市每日最高气温如图所示,则下列说法错误的是( )
A、等腰三角形 B、直角三角形 C、矩形 D、菱形29. 5月1日至7日,我市每日最高气温如图所示,则下列说法错误的是( ) A、中位数是33℃ B、众数是33℃ C、平均数是 ℃ D、4日至5日最高气温下降幅度较大30. 已知平面内有⊙O和点A , B , 若⊙O半径为2cm , 线段OA=3cm , OB=2cm , 则直线AB与⊙O的位置关系为( )A、相离 B、相交 C、相切 D、相交或相切31. 如图,在△ABC中,∠BAC=90°,AB=AC=5,点D在AC上,且AD=2,点E是AB上的动点,连结DE , 点F , G分别是BC和DE的中点,连结AG , FG , 当AG=FG时,线段DE长为( )
A、中位数是33℃ B、众数是33℃ C、平均数是 ℃ D、4日至5日最高气温下降幅度较大30. 已知平面内有⊙O和点A , B , 若⊙O半径为2cm , 线段OA=3cm , OB=2cm , 则直线AB与⊙O的位置关系为( )A、相离 B、相交 C、相切 D、相交或相切31. 如图,在△ABC中,∠BAC=90°,AB=AC=5,点D在AC上,且AD=2,点E是AB上的动点,连结DE , 点F , G分别是BC和DE的中点,连结AG , FG , 当AG=FG时,线段DE长为( )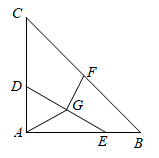 A、 B、 C、 D、432. 已知点P(a , b)在直线y=﹣3x﹣4上,且2a﹣5b≤0,则下列不等式一定成立的是( )A、 ≤ B、 ≥ C、 ≥ D、 ≤33. 如图,AB是⊙O的直径,弦CD⊥OA于点E,连结OC,OD.若⊙O的半径为m,∠AOD=∠α,则下列结论一定成立的是( )
A、 B、 C、 D、432. 已知点P(a , b)在直线y=﹣3x﹣4上,且2a﹣5b≤0,则下列不等式一定成立的是( )A、 ≤ B、 ≥ C、 ≥ D、 ≤33. 如图,AB是⊙O的直径,弦CD⊥OA于点E,连结OC,OD.若⊙O的半径为m,∠AOD=∠α,则下列结论一定成立的是( )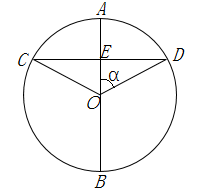 A、oE=m•tanα B、CD=2m•sinα C、AE=m•cosα D、S△COD=m2•sinα34. 一杠杆装置如图,杆的一端吊起一桶水,水桶对杆的拉力的作用点到支点的杆长固定不变.甲、乙、丙、丁四位同学分别在杆的另一端竖直向下施加压力F甲、F乙、F丙、F丁 , 将相同重量的水桶吊起同样的高度,若F乙<F丙<F甲<F丁 , 则这四位同学对杆的压力的作用点到支点的距离最远的是( )
A、oE=m•tanα B、CD=2m•sinα C、AE=m•cosα D、S△COD=m2•sinα34. 一杠杆装置如图,杆的一端吊起一桶水,水桶对杆的拉力的作用点到支点的杆长固定不变.甲、乙、丙、丁四位同学分别在杆的另一端竖直向下施加压力F甲、F乙、F丙、F丁 , 将相同重量的水桶吊起同样的高度,若F乙<F丙<F甲<F丁 , 则这四位同学对杆的压力的作用点到支点的距离最远的是( ) A、甲同学 B、乙同学 C、丙同学 D、丁同学35. 如图,在Rt△ABC纸片中,∠ACB=90°,AC=4,BC=3,点D , E分别在AB , AC上,连结DE , 将△ADE沿DE翻折,使点A的对应点F落在BC的延长线上,若FD平分∠EFB , 则AD的长为( )
A、甲同学 B、乙同学 C、丙同学 D、丁同学35. 如图,在Rt△ABC纸片中,∠ACB=90°,AC=4,BC=3,点D , E分别在AB , AC上,连结DE , 将△ADE沿DE翻折,使点A的对应点F落在BC的延长线上,若FD平分∠EFB , 则AD的长为( )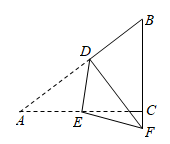 A、 B、 C、 D、
A、 B、 C、 D、