2022届中考数学 二轮必刷填空题 全国通用
试卷更新日期:2022-03-08 类型:二轮复习
一、填空题
-
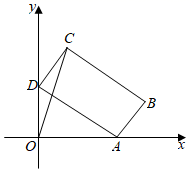
1. 如图,矩形 , , ,点 在 轴正半轴上,点 在 轴正半轴上.当点 在 轴上运动时,点 也随之在 轴上运动,在这个运动过程中,点 到原点 的最大距离为 .
 2. 已知非负实数 , , 满足 ,设 的最大值为 ,最小值为 ,则 的值为 .3. 已知,在 中, , , ,则 的面积为.4. 若实数 满足 ,则 .5. 若关于x的一元二次方程ax2+4x﹣2=0有实数根,则a的取值范围为 .6. 如图,矩形 中, , ,对角线 的垂直平分线 交 于点 、交 于点 ,则线段 的长为.
2. 已知非负实数 , , 满足 ,设 的最大值为 ,最小值为 ,则 的值为 .3. 已知,在 中, , , ,则 的面积为.4. 若实数 满足 ,则 .5. 若关于x的一元二次方程ax2+4x﹣2=0有实数根,则a的取值范围为 .6. 如图,矩形 中, , ,对角线 的垂直平分线 交 于点 、交 于点 ,则线段 的长为.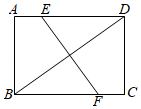 7. 如图,在菱形 中, , 为 中点,点 在 延长线上, 、 分别为 、 中点, , ,则 .
7. 如图,在菱形 中, , 为 中点,点 在 延长线上, 、 分别为 、 中点, , ,则 .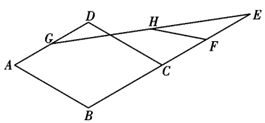 8. 若点 、 、 都在反比例函数 (k为常数)的图象上,则 、 、 的大小关系为 .9. 在平面直角坐标系中,一次函数 与反比例函数 的图象交于 , 两点,则 的值是.10. 如图,在平面直角坐标系中,以 为圆心,AB为直径的圆与x轴相切,与y轴交于A,C两点,则点B的坐标是.
8. 若点 、 、 都在反比例函数 (k为常数)的图象上,则 、 、 的大小关系为 .9. 在平面直角坐标系中,一次函数 与反比例函数 的图象交于 , 两点,则 的值是.10. 如图,在平面直角坐标系中,以 为圆心,AB为直径的圆与x轴相切,与y轴交于A,C两点,则点B的坐标是. 11. 若 在实数范围内有意义,则x的取值范围是 .12. 如图,在圆内接五边形ABCDE中,∠EAB∠+∠C+∠CDE+∠E=430°,则∠CDA=度.
11. 若 在实数范围内有意义,则x的取值范围是 .12. 如图,在圆内接五边形ABCDE中,∠EAB∠+∠C+∠CDE+∠E=430°,则∠CDA=度. 13. 已知函数y 的图象如图所示,若直线y=kx﹣3与该图象有公共点,则k的最大值与最小值的和为 .
13. 已知函数y 的图象如图所示,若直线y=kx﹣3与该图象有公共点,则k的最大值与最小值的和为 .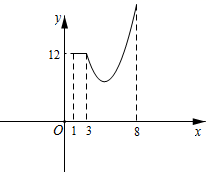 14. y与x之间的函数关系可记为y=f(x).例如:函数y=x2可记为f(x)=x2.若对于自变量取值范围内的任意一个x,都有f(﹣x)=f(x),则f(x)是偶函数;若对于自变量取值范围内的任意一个x,都有f(﹣x)=﹣f(x),则f(x)是奇函数.例如:f(x)=x2是偶函数,f(x) 是奇函数.若f(x)=ax2+(a﹣5)x+1是偶函数,则实数a=.15. 如图, 的顶点B在反比例函数 的图象上,顶点C在x轴负半轴上, 轴,AB , BC分别交y轴于点D , E . 若 , ,则 .
14. y与x之间的函数关系可记为y=f(x).例如:函数y=x2可记为f(x)=x2.若对于自变量取值范围内的任意一个x,都有f(﹣x)=f(x),则f(x)是偶函数;若对于自变量取值范围内的任意一个x,都有f(﹣x)=﹣f(x),则f(x)是奇函数.例如:f(x)=x2是偶函数,f(x) 是奇函数.若f(x)=ax2+(a﹣5)x+1是偶函数,则实数a=.15. 如图, 的顶点B在反比例函数 的图象上,顶点C在x轴负半轴上, 轴,AB , BC分别交y轴于点D , E . 若 , ,则 .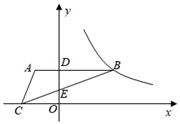 16. 如图,矩形ABCD中, ,对角线AC , BD交于点O , ,垂足为点H , 若 ,则AD的长为 .
16. 如图,矩形ABCD中, ,对角线AC , BD交于点O , ,垂足为点H , 若 ,则AD的长为 .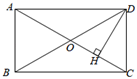 17. 如图, ,定长为a的线段端点A , B分别在射线OP , OQ上运动(点A , B不与点O重合),C为AB的中点,作 关于直线OC对称的 , 交AB于点D , 当 是等腰三角形时, 的度数为 .
17. 如图, ,定长为a的线段端点A , B分别在射线OP , OQ上运动(点A , B不与点O重合),C为AB的中点,作 关于直线OC对称的 , 交AB于点D , 当 是等腰三角形时, 的度数为 .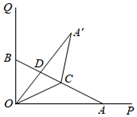 18. 如图,在平面直角坐标系中,点A的坐标为(5,0),点M的坐标为(0,4),过点M作MN x轴,点P在射线MN上,若 MAP为等腰三角形,则点P的坐标为 .
18. 如图,在平面直角坐标系中,点A的坐标为(5,0),点M的坐标为(0,4),过点M作MN x轴,点P在射线MN上,若 MAP为等腰三角形,则点P的坐标为 . 19. 因式分解:﹣3am2+12an2= .20. 如图,⊙A、⊙B、⊙C两两不相交,且半径都是2cm,则图中三个扇形(即阴影部分)面积之和是cm2
19. 因式分解:﹣3am2+12an2= .20. 如图,⊙A、⊙B、⊙C两两不相交,且半径都是2cm,则图中三个扇形(即阴影部分)面积之和是cm2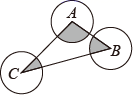 21. 如图,在平面直角坐标系 中,点A在 轴负半轴上,点B在 轴正半轴上,⊙D经过A , B , O , C四点,∠ACO=120°,AB=4,则圆心点D的坐标是
21. 如图,在平面直角坐标系 中,点A在 轴负半轴上,点B在 轴正半轴上,⊙D经过A , B , O , C四点,∠ACO=120°,AB=4,则圆心点D的坐标是 22. 如图,四边形ABCD是平行四边形,以点B为圆心,BC的长为半径作弧交AD于点E , 分别以点C , E为圆心,大于 的长为半径作弧,两弧交于点P , 作射线BP交AD的延长线于点F , ∠CBE=60°,BC=6,则BF的长为
22. 如图,四边形ABCD是平行四边形,以点B为圆心,BC的长为半径作弧交AD于点E , 分别以点C , E为圆心,大于 的长为半径作弧,两弧交于点P , 作射线BP交AD的延长线于点F , ∠CBE=60°,BC=6,则BF的长为 23. 正六边形的一个内角是正n边形一个外角的4倍,则n= .24. 如图,已知 ,则 .
23. 正六边形的一个内角是正n边形一个外角的4倍,则n= .24. 如图,已知 ,则 . 25. 六个带 角的直角三角板拼成一个正六边形,直角三角板的最短边为1,求中间正六边形的面积 .
25. 六个带 角的直角三角板拼成一个正六边形,直角三角板的最短边为1,求中间正六边形的面积 .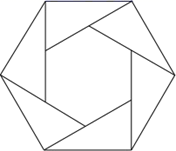 26. 某人购进一批苹果到集贸市场零售,已知卖出的苹果数量与售价之间的关系如图所示,成本为5元/千克,现以8元/千克卖出,赚元.
26. 某人购进一批苹果到集贸市场零售,已知卖出的苹果数量与售价之间的关系如图所示,成本为5元/千克,现以8元/千克卖出,赚元.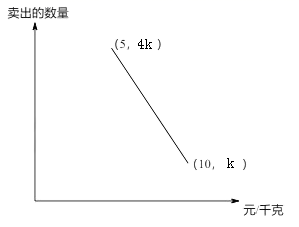 27. 如图是一架梯子的示意图,其中AA1∥BB1∥CC1∥DD1 , 且AB=BC=CD.为使其更稳固,在A,D1间加绑一条安全绳(线段AD1)量得AE=0.4m,则AD1=m.
27. 如图是一架梯子的示意图,其中AA1∥BB1∥CC1∥DD1 , 且AB=BC=CD.为使其更稳固,在A,D1间加绑一条安全绳(线段AD1)量得AE=0.4m,则AD1=m.