四川省遂宁市2021-2022学年高二下学期理数开学考试试卷

试卷更新日期：2022-03-08 类型：开学考试

进入出卷网下载

一、单选题

1. 直线 $3 x - \sqrt{3} y - 1 = 0$ 的倾斜角为（）

A、150º B、30º C、120º D、60º

查看试题解析
2. 命题“ $\forall x \in R$ ， ${(\frac{1}{3})}^{x} > 0$ ”的否定是（）

A、 $\exists x_{0} \in R$ ， B、 $\forall x \in R$ ， ${(\frac{1}{3})}^{x} \leq 0$ C、 $\forall x \in R$ ， ${(\frac{1}{3})}^{x} < 0$ D、 $\exists x_{0} \in R$ ， ${(\frac{1}{3})}^{x_{0}} \leq 0$

查看试题解析
3. 设 $m ， n$ 是两条不同的直线， $α ， β$ 是两个不同的平面，且 $m \subset α ， n \subset β$ ，则下列命题正确的是（）
① 若 $m // β ， n // α$ ，则 $α // β$ ②若 $m ⊥ β$ ，则 $α ⊥ β$ ③若 $α // β$ ，则 $m // β ， n // α$ ④若 $α ⊥ β$ ，则 $m ⊥ β ， n ⊥ α$

A、①③ B、①④ C、②③ D、②④

查看试题解析
4. 某企业生产某种产品，其广告层面的投入为x（单位：百万元），该企业产生的利润为y（单位：百万元），经统计得到如下表格中的数据：经计算广告投入x与利润y满足线性回归方程： $\hat{y} = 6.5 x + 17.5$ ，则t的值为（）

x

2

4

5

6

8

y

30

40

60

t

70

A、45 B、50 C、56.5 D、65

查看试题解析
5. 已知三棱柱 $A B C - A_{1} B_{1} C_{1}$ 的底面是边长为2的等边三角形，侧棱长为3， $A_{1}$ 在底面ABC上的射影D为BC的中点，则异面直线AB与 $C C_{1}$ 所成的角的为（）

A、 $\frac{π}{6}$ B、 $\frac{π}{4}$ C、 $\frac{π}{3}$ D、 $\frac{π}{2}$

查看试题解析
6. 若直线 $l_{1} ： (m + 1) x + 6 y + 4 = 0$ 与 $l_{2} ： x + 3 m y + 1 = 0$ 平行，则m的值为（）

A、－2 B、－1或－2 C、1或－2 D、1

查看试题解析
7. 执行如图所示的程序框图，输出的值为（）

A、 $\frac{4}{5}$ B、 $\frac{5}{6}$ C、 $\frac{5}{7}$ D、 $\frac{6}{7}$

查看试题解析
8. 设x，y满足约束条件 ${\begin{array}{l} x + 3 y \leq 3 \\ x - y \geq 1 \\ y \geq 0 \end{array}$ ，则 $z = \frac{y}{x}$ 的最大值为（）

A、0 B、1 C、 $\frac{1}{2}$ D、 $\frac{1}{3}$

查看试题解析
9. 设点P为直线 $2 x + y - 2 = 0$ 上的点，过点P作圆C： $x^{2} + y^{2} + 2 x + 2 y - 2 = 0$ 的两条切线，切点分别为A，B，当四边形PACB的面积取得最小值时，此时直线AB的方程为（）

A、 $2 x - y - 1 = 0$ B、 $2 x + y - 1 = 0$ C、 $2 x - y + 1 = 0$ D、 $2 x + y + 1 = 0$

查看试题解析
10. 近期，新冠疫苗第三针加强针开始接种，接种后需要在留观室留观满半小时后才能离开.甲､乙两人定于某日上午前往同一医院接种，该医院上午上班时间为7：30，开始接种时间为8：00，截止接种时间为11：30.假设甲､乙在上午时段内的任何时间到达医院是等可能的，因接种人数较少，接种时间忽略不计.则甲､乙两人在留观室相遇的概率是（）

A、 $\frac{13}{49}$ B、 $\frac{36}{49}$ C、 $\frac{1}{7}$ D、 $\frac{6}{7}$

查看试题解析
11. 我国古代数学名著《九章算术》中有堑堵一说，“堑堵”意指底面为直角三角形，且侧棱垂直于底面的三棱柱，如图所示的“堑堵” $A B C - A_{1} B_{1} C_{1}$ 中， $∠ A C B = 90 °$ ， $A B = A A_{1} = 2$ ， $A C = B C$ ，则“堑堵”的外接球的表面积为（）

A、8π B、4π C、 $2 \sqrt{2} π$ D、2π

查看试题解析
12. 设函数 $f (x) = a x + \frac{x}{x - 1} (x > 1)$ ，若 $a$ 是从 $0 ， 1 ， 2$ 三个数中任取一个， $b$ 是从 $1 ， 2 ， 3 ， 4 ， 5$ 五个数中任取一个，那么 $f (x) > b$ 恒成立的概率是（）

A、 $\frac{3}{5}$ B、 $\frac{7}{15}$ C、 $\frac{2}{5}$ D、 $\frac{1}{2}$

查看试题解析

二、填空题

13. 某创新企业为了解新研发的一种产品的销售情况，从编号为01，02，…，80的80个专卖店销售数据中，采用系统抽样的方法抽取一个样本，若样本中的个体编号依次为03，13，…则样本中的最后一个个体编号是.

查看试题解析
14. 某甲､乙两人练习跳绳，每人练习10组，每组不间断跳绳计数的茎叶图如图，则下面结论中所有正确的序号是.
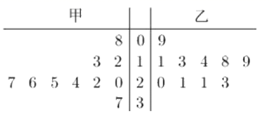
①甲比乙的极差大；②乙的中位数是18；③甲的平均数比乙的大；④乙的众数是21.

查看试题解析
15. 直线l ： y=-x+m与曲线 $x = \sqrt{4 - y^{2}}$ 有两个公共点，则实数m的取值范围是.

查看试题解析
16. 已知平面上任意一点 $P (x_{0} ， y_{0})$ ，直线 $l ： y = k x + b$ ，则点P到直线l的距离为 $d = \frac{| k x_{0} - y_{0} + b |}{\sqrt{1 + k^{2}}}$ ；当点 $P (x_{0} ， y_{0})$ 在函数 $y = f (x)$ 图象上时，点P到直线l的距离为 $d = \frac{| k x_{0} - f (x_{0}) + b |}{\sqrt{1 + k^{2}}}$ ，请参考该公式求出 $| x + 3 - \sqrt{1 - x^{2}} | + | t - 3 + \sqrt{1 - t^{2}} | (x ， t \in R)$ 的最小值为．

查看试题解析

三、解答题

17. 已知直线 $l ： 2 x + 3 y - 6 = 0$

(1)、求过点 $P (2 ， 3)$ ，且与直线 $l$ 平行的直线 $m$ 的方程；

(2)、直线 $l$ 与圆 $C ： x^{2} + y^{2} - 2 x - 4 y + 4 = 0$ 相交于 $A ､ B$ 两点，求线段 $A B$ 的长.

查看试题解析
18. “十一五”规划提出单位国内生产总值（GDP）能耗降低20%左右的目标，“节能降耗”需要长期推行，这既有利于改善环境､可持续发展，又有利于民众生活福祉的改善.下表提供了某厂节能降耗技术改造后生产过程中记录的产量x（吨）与相应的生产能耗y（吨标准煤）的几组对照数据：

x

3

4

5

6

7

y

2.7

3.5

4.1

4.7

5

参考公式：回归方程 $\hat{y} = \hat{b} x + \hat{a}$ 中斜率和截距的最小二乘估计公式分别为 $\hat{b} = \frac{\sum_{i = 1}^{n} (x_{i} - \bar{x}) (y_{i} - \bar{y})}{\sum_{i = 1}^{n} {(x_{i} - \bar{x})}^{2}} = \frac{\sum_{i = 1}^{n} x_{i} y_{i} - n \bar{x} \bar{y}}{\sum_{i = 1}^{n} x_{i}^{2} - n {\bar{x}}^{2}}$ ， $\hat{a} = \bar{y} - \hat{b} x$ .

(1)、请根据上表提供的数据，求出y关于x的线性回归方程 $\hat{y} = \hat{b} x + \hat{a}$ ；

(2)、当该厂产量提升到10吨时，预测生产能耗为多少.

查看试题解析
19. 在正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $M$ ， $N$ ， $E$ 分别是 $A B$ ， $D D_{1}$ ， $A A_{1}$ 的中点.

(1)、证明：平面 $M N E ∥$ 平面 $B C D_{1}$ ；

(2)、求直线 $M N$ 与 $D_{1} C$ 所成角的正切值.

查看试题解析
20. 某保险公司决定每月给推销员确定具体的销售目标，对推销员实行目标管理.销售目标确定的适当与否，直接影响公司的经济效益和推销员的工作积极性，为此，该公司当月随机抽取了50位推销员上个月的月销售额（单位：万元），绘制成如图所示的频率分布直方图：

(1)、①根据图中数据，求出月销售额在 $[14 ， 16)$ 小组内的频率；
②根据直方图估计，月销售目标定为多少万元时，能够使70%的推销员完成任务？并说明理由；

(2)、该公司决定从月销售额为 $[22 ， 24)$ 和 $[24 ， 26)$ 的两个小组中，选取2位推销员介绍销售经验，求选出的推销员来自同一个小组的概率.

查看试题解析
21. 如图，在直三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中，平面 $A_{1} B C ⊥$ 侧面 $A B B_{1} A_{1}$ ，且 $A A_{1} = A B = 2$ .

(1)、求证： $A B ⊥ B C$ ；

(2)、若直线 $A C$ 与平面 $A_{1} B C$ 所成的角为 $\frac{π}{6}$ ，请问在线段 $A_{1} C$ 上是否存在点 $E$ ，使得二面角 $A - B E - C$ 的大小为 $\frac{2 π}{3}$ ，若存在请求出 $E$ 的位置，不存在请说明理由.

查看试题解析
22. 已知直线 $l ： x = m y - 1$ ，圆 $C ： x^{2} + y^{2} + 4 x = 0$ .

(1)、证明：直线l与圆C相交；

(2)、设l与C的两个交点分别为A、B，弦AB的中点为M，求点M的轨迹方程；

(3)、在（2）的条件下，设圆C在点A处的切线为 $l_{1}$ ，在点B处的切线为 $l_{2}$ ， $l_{1}$ 与 $l_{2}$ 的交点为Q.试探究：当m变化时，点Q是否恒在一条定直线上？若是，请求出这条直线的方程；若不是，说明理由.

查看试题解析

x	3	4	5	6	7
y	2.7	3.5	4.1	4.7	5