湖南省长沙市长郡教育集团2021-2022学年九年级下学期入学考试数学试卷
试卷更新日期:2022-03-08 类型:开学考试
一、单选题
-
1. 下列事件中,是必然事件的是( )A、购买一张彩票,中奖 B、射击运动员射击一次,命中靶心 C、经过有交通信号灯的路口,遇到红灯 D、任意画一个三角形,其内角和是180°2. 下列四个几何体中,左视图为圆的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列命题是真命题的是( )A、五边形的内角和是720° B、三角形的任意两边之和大于第三边 C、内错角相等 D、对角线互相垂直的四边形是菱形4. 一个不透明的盒子中装有4个形状、大小质地完全相同的小球,这些小球上分别标有数字-1、0、2和3.从中随机地摸取一个小球,则这个小球所标数字是正数的概率为( )A、 B、 C、 D、5. 如图,四边形ABCD内接于 ,若∠BOD=144°,则∠C的度数是( )
3. 下列命题是真命题的是( )A、五边形的内角和是720° B、三角形的任意两边之和大于第三边 C、内错角相等 D、对角线互相垂直的四边形是菱形4. 一个不透明的盒子中装有4个形状、大小质地完全相同的小球,这些小球上分别标有数字-1、0、2和3.从中随机地摸取一个小球,则这个小球所标数字是正数的概率为( )A、 B、 C、 D、5. 如图,四边形ABCD内接于 ,若∠BOD=144°,则∠C的度数是( ) A、14° B、36° C、72° D、108°6. 下列关于x的一元二次方程,一定有两个不相等的实数根的是( )A、x2+kx﹣1=0 B、x2+kx+1=0 C、x2+x﹣k=0 D、x2+x+k=07. 抛物线y=2x2-2 x+1与坐标轴的交点个数是( )A、0 B、1 C、2 D、38. A(-3,2)关于原点的对称点是B,B关于x轴的对称点是C,则点C的坐标是( )A、(3,2) B、(-3,2) C、(3,-2) D、(-2,3)9. 如图,在Rt△ABC中,∠C=90°,AB=10,cos∠B= ,则BC=( )
A、14° B、36° C、72° D、108°6. 下列关于x的一元二次方程,一定有两个不相等的实数根的是( )A、x2+kx﹣1=0 B、x2+kx+1=0 C、x2+x﹣k=0 D、x2+x+k=07. 抛物线y=2x2-2 x+1与坐标轴的交点个数是( )A、0 B、1 C、2 D、38. A(-3,2)关于原点的对称点是B,B关于x轴的对称点是C,则点C的坐标是( )A、(3,2) B、(-3,2) C、(3,-2) D、(-2,3)9. 如图,在Rt△ABC中,∠C=90°,AB=10,cos∠B= ,则BC=( ) A、6 B、8 C、9 D、1510. 如图,菱形ABCD的边长为10,面积为80,∠BAD<90°,⊙O与边AB,AD都相切菱形的顶点A到圆心O的距离为5,则⊙O的半径长等于( )
A、6 B、8 C、9 D、1510. 如图,菱形ABCD的边长为10,面积为80,∠BAD<90°,⊙O与边AB,AD都相切菱形的顶点A到圆心O的距离为5,则⊙O的半径长等于( )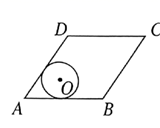 A、2.5 B、 C、 D、3
A、2.5 B、 C、 D、3二、填空题
-
11. 在一个不透明的盒子中装有n个规格相同的乒乓球,其中有2个黄色球,每次摸球前先将盒中的球摇匀,随机摸出一个球记下颜色后再放回盒中,通过大量重复试验后发现,摸到黄色球的频率稳定于0.2,那么可以推算出n大约是 .
12. 在比例尺为1:200的地图上,测得A,B两地间的图上距离为4.5cm,则A,B两地间的实际距离为m.13. 如图,在同一时刻,测得小华和旗杆的影长分别为1m和6m,小华的身高约为1.6m,则旗杆的高约为m.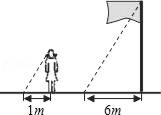 14. 飞机着陆后滑行的距离S(单位:m)关于滑行时间t(单位:s)的函数解析式是 ,则飞机着陆后滑行s后,才会停下来.15. 如图所示,AB是⊙O的直径,弦CD⊥AB于H,∠A=30°,OH=1,则⊙O的半径是.
14. 飞机着陆后滑行的距离S(单位:m)关于滑行时间t(单位:s)的函数解析式是 ,则飞机着陆后滑行s后,才会停下来.15. 如图所示,AB是⊙O的直径,弦CD⊥AB于H,∠A=30°,OH=1,则⊙O的半径是. 16. 如图所示,在Rt△ABO中,∠AOB=90°,点A在第一象限,点B在第四象限,且 ,若点A(x0 , y0)的坐标满足 ,则点B(x,y)的坐标所满足的关系式为.
16. 如图所示,在Rt△ABO中,∠AOB=90°,点A在第一象限,点B在第四象限,且 ,若点A(x0 , y0)的坐标满足 ,则点B(x,y)的坐标所满足的关系式为.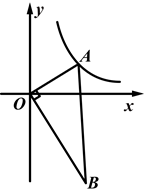
三、解答题
-
17. .18. 先化简再求值: ,其中 .19. 已知一元二次方程 .(1)、若方程有两个实数根,求m的范围;(2)、若方程的两个实数根为 ,且 ,求m的值.20. 为了传承中华优秀传统文化,市教育局决定开展“经典诵读进校园”活动,某校团委组织八年级100名学生进行“经典诵读”选拔赛,赛后对全体参赛学生的成绩进行整理,得到下列不完整的统计图表.
组别
分数段
频次
频率
A
60≤x<70
17
0.17
B
70≤x<80
30
a
C
80≤x<90
b
0.45
D
90≤x<100
8
0.08
请根据所给信息,解答以下问题:
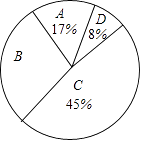 (1)、表中a= , b=;(2)、请计算扇形统计图中B组对应扇形的圆心角的度数;(3)、已知有四名同学均取得98分的最好成绩,其中包括来自同一班级的甲、乙两名同学,学校将从这四名同学中随机选出两名参加市级比赛,请用列表法或画树状图法求甲、乙两名同学都被选中的概率.21. 如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)、表中a= , b=;(2)、请计算扇形统计图中B组对应扇形的圆心角的度数;(3)、已知有四名同学均取得98分的最好成绩,其中包括来自同一班级的甲、乙两名同学,学校将从这四名同学中随机选出两名参加市级比赛,请用列表法或画树状图法求甲、乙两名同学都被选中的概率.21. 如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.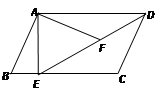 (1)、求证:△ADF∽△DEC(2)、若AB=4,AD=3 ,AE=3,求AF的长.22. 某网店销售一种文具袋,成本为30元/件,每天的销售量 (件)与销售单价 (元)之间满足一次函数关系,其图象如图所示.
(1)、求证:△ADF∽△DEC(2)、若AB=4,AD=3 ,AE=3,求AF的长.22. 某网店销售一种文具袋,成本为30元/件,每天的销售量 (件)与销售单价 (元)之间满足一次函数关系,其图象如图所示. (1)、求 与 之间的函数关系式;(2)、如果规定每天的销量不低于240件,那么当销售单价为多少元时,每天获取的利润最大?最大利润是多少?23. 如图,在Rt△ABC中,∠BAC=90°,D为BC上的一点,以AD为直径的 交AB于E,连接CE交 于G,连接DG,∠ACB=∠EGD.
(1)、求 与 之间的函数关系式;(2)、如果规定每天的销量不低于240件,那么当销售单价为多少元时,每天获取的利润最大?最大利润是多少?23. 如图,在Rt△ABC中,∠BAC=90°,D为BC上的一点,以AD为直径的 交AB于E,连接CE交 于G,连接DG,∠ACB=∠EGD.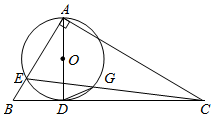 (1)、证明:BC与 相切;(2)、若BD=2,CD=6,求 的直径AD;(3)、在(2)的条件下,求EC.24. 在平面直角坐标系中,将一点(横坐标与纵坐标不相等)横坐标与纵坐标互换后得到的点叫这一点的“H点”,如(2,-3)与(-3,2)是一对“H点”.(1)、点 和它的“H点”均在直线 上,求k的值;(2)、若直线 经过的A,B两点恰好是一对“H点”,其中点A还在反比例函数 的图象上,一条抛物线 也经过A,B两点,求该抛物线的解析式;(3)、已知 ,B为抛物线 上的一对“H点”,且满足: , ,点P为抛物线上一动点,若该抛物线上有且仅存在3个点P满足△PAB的面积为16,求 的值.25. 在平面直角坐标系中,点O为坐标原点,抛物线 交x轴的负半轴于点A,交x轴的正半轴于点B,交y轴的正半轴于点C,且OB=2OC.
(1)、证明:BC与 相切;(2)、若BD=2,CD=6,求 的直径AD;(3)、在(2)的条件下,求EC.24. 在平面直角坐标系中,将一点(横坐标与纵坐标不相等)横坐标与纵坐标互换后得到的点叫这一点的“H点”,如(2,-3)与(-3,2)是一对“H点”.(1)、点 和它的“H点”均在直线 上,求k的值;(2)、若直线 经过的A,B两点恰好是一对“H点”,其中点A还在反比例函数 的图象上,一条抛物线 也经过A,B两点,求该抛物线的解析式;(3)、已知 ,B为抛物线 上的一对“H点”,且满足: , ,点P为抛物线上一动点,若该抛物线上有且仅存在3个点P满足△PAB的面积为16,求 的值.25. 在平面直角坐标系中,点O为坐标原点,抛物线 交x轴的负半轴于点A,交x轴的正半轴于点B,交y轴的正半轴于点C,且OB=2OC. (1)、求点B的坐标和a的值;(2)、如图1,点D,P分别在一、三象限的抛物线上,其中点P的横坐标为t,连接BP,交y轴于点E,连接CD,DE,设△CDE的面积为s,若 ,求点D的坐标;(3)、如图2,在(2)的条件下,将线段DE绕点D逆时针旋转90°得到线段DF,射线AE与射线FB交于点G,连接AP,若∠AGB=2∠APB,求点P的坐标.
(1)、求点B的坐标和a的值;(2)、如图1,点D,P分别在一、三象限的抛物线上,其中点P的横坐标为t,连接BP,交y轴于点E,连接CD,DE,设△CDE的面积为s,若 ,求点D的坐标;(3)、如图2,在(2)的条件下,将线段DE绕点D逆时针旋转90°得到线段DF,射线AE与射线FB交于点G,连接AP,若∠AGB=2∠APB,求点P的坐标.