四川省达州市渠县2021-2022学年七年级上学期期末数学试卷
试卷更新日期:2022-03-08 类型:期末考试
一、单选题
-
1. 下列各图中表示线段 ,射线 的是( )A、
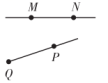
B、
B、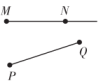
C、
C、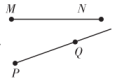
D、
D、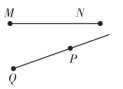
2. 下列式子中,不能成立的是( )A、﹣(﹣3)=3 B、﹣|﹣4|=﹣4 C、33=9 D、(﹣2)2=43. 如图是由5个小立方块搭成的几何体,则该几何体从左面看到的形状图是( )
2. 下列式子中,不能成立的是( )A、﹣(﹣3)=3 B、﹣|﹣4|=﹣4 C、33=9 D、(﹣2)2=43. 如图是由5个小立方块搭成的几何体,则该几何体从左面看到的形状图是( ) A、
A、 B、
B、 C、
C、 D、
D、 4. 若3am+3bn+2与﹣2a5b是同类项,则mn=( )A、-1 B、-2 C、2 D、15. 平面内存在线段AB和点P,由下列条件一定能得到“P是线段AB的中点”的是( )A、AP= AB B、AB=2PB C、AP=PB D、AP=PB= AB6. 下列说法中正确的是( )A、 是单项式 B、 不是单项式 C、﹣2πab2的系数是﹣2 D、﹣32xy2的次数是57. 在解方程 +x= 时,在方程的两边同时乘以6,去分母正确的是( )A、2(x﹣1)+6x=3(3x+1) B、2x﹣1+6x=3(3x+1) C、2(x﹣1)+x=3(3x+1) D、(x﹣1)+6x=3(3x+1)8. 如果在数轴上表示a,b两个实数的点的位置如图所示,那么|a﹣b|+|a+b|化简的结果为( )
4. 若3am+3bn+2与﹣2a5b是同类项,则mn=( )A、-1 B、-2 C、2 D、15. 平面内存在线段AB和点P,由下列条件一定能得到“P是线段AB的中点”的是( )A、AP= AB B、AB=2PB C、AP=PB D、AP=PB= AB6. 下列说法中正确的是( )A、 是单项式 B、 不是单项式 C、﹣2πab2的系数是﹣2 D、﹣32xy2的次数是57. 在解方程 +x= 时,在方程的两边同时乘以6,去分母正确的是( )A、2(x﹣1)+6x=3(3x+1) B、2x﹣1+6x=3(3x+1) C、2(x﹣1)+x=3(3x+1) D、(x﹣1)+6x=3(3x+1)8. 如果在数轴上表示a,b两个实数的点的位置如图所示,那么|a﹣b|+|a+b|化简的结果为( ) A、2a B、﹣2a C、0 D、2b9. 在某市2021年青少年航空航天模型锦标赛中,各年龄组的参赛人数情况如下表所示:
A、2a B、﹣2a C、0 D、2b9. 在某市2021年青少年航空航天模型锦标赛中,各年龄组的参赛人数情况如下表所示:年龄组
13岁
14岁
15岁
16岁
参赛人数
5
19
12
14
若小明所在年龄组的参赛人数占全体参赛人数的38%,则小明所在的年龄组是( )
A、13岁 B、14岁 C、15岁 D、16岁10. 整式 的值随 的取值不同而不同,下表是当 取不同值时对应的整式的值:-2
-1
0
1
2
-12
-8
-4
0
4
则关于 的方程 的解为( )
A、 B、 C、 D、二、填空题
-
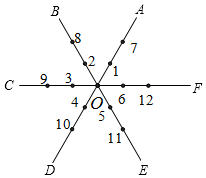
11. 用代数式表示:比x与y的和的平方小x的数为 .12. 根据央视报道,去年我国汽车尾气排放总量大约为47000000吨.将47000000用科学记数法表示为.13. 已知关于x的方程5x﹣2=3x+16的解与方程4a+1=4(x+a)﹣5a的解相同,则a=.14. 已知a>0,b<0且a+b<0,那么有理数a,b,﹣a,|b|的大小关系是 .(用“<”号连接)15. 如图,平面内有公共端点的六条射线,OB,OC,OD,OE,OF,从射线OA开始按逆时针方向依次在射线上写出数字1,2,3,4,5,6,7,….则“2021”在射线 上.
 16. 某超市在“五一”活动期间,推出如下购物优惠方案:
16. 某超市在“五一”活动期间,推出如下购物优惠方案:①一次性购物在100元(不含100元)以内,不享受优惠;
②一次性购物在100元(含100元)以上,350元(不含350元)以内,一律享受九折优惠;
③一次性购物在350元(含350元)以上,一律享受八折优惠.小敏在该超市两次购物分别付款70元和288元,如果小敏把这两次购物改为一次性购物,则应付款元.
三、解答题
-
17. 计算:(1)、(2)、18. 解方程:(1)、4x﹣3(20﹣x)=﹣4;(2)、 .19. 已知 的值是7,求代数式 的值.20. 如图,是底面为正方形的长方体的表面展开图,折叠成一个长方体,那么:
 (1)、与N重合的点是哪几个?(2)、若AB=3cm,AH=5cm,则该长方体的表面积和体积分别是多少?21. 某校组织1002名学生参加“展示我美丽祖国”庆国庆的自拍照片的评比活动.随机抽取一些学生在评比中的成绩制成的统计图表如表:
(1)、与N重合的点是哪几个?(2)、若AB=3cm,AH=5cm,则该长方体的表面积和体积分别是多少?21. 某校组织1002名学生参加“展示我美丽祖国”庆国庆的自拍照片的评比活动.随机抽取一些学生在评比中的成绩制成的统计图表如表:
频数分布表
分数段
频数
百分比
80≤x<85
a
20%
85≤x<90
80
b
90≤x<95
60
30%
95≤x<100
20
根据以上图表提供的信息,解答下列问题:
(1)、写出表中a、b的数值:a= , b=;(2)、补全频数分布表和频数分布直方图;(3)、如果评比成绩在95分以上的可以获得一等奖,试估计该校参加此次活动获得一等奖的人数.22. 正方形ABCD的轨道上有两个点甲与乙,开始时甲在A处,乙在C处,它们沿着正方形轨道顺时针同时出发,甲的速度为每秒1cm,乙的速度为每秒5cm.已知正方形轨道ABCD的边长为2cm,求乙在第5次追上甲时在哪条线段上? 23. 阅读下面材料:
23. 阅读下面材料:数学课上,老师给出了如下问题:

如图1,∠AOB=80°,OC平分∠AOB,若∠BOD=20°,请你补全图形,并求∠COD的度数.
以下是小明的解答过程:
解:如图2,因为OC平分∠AOB,∠AOB=80°,
所以∠BOC=_____∠AOB=_____°
因为∠BOD=20°,
所以∠COD=______°
小静说:“我觉得这个题有两种情况,小明考虑的是OD在∠AOB外部的情况,事实上,OD还可能在∠AOB的内部”.
完成以下问题:
(1)、请你将小明的解答过程补充完整;(2)、根据小静的想法,请你在图3中画出另一种情况对应的图形,并直接写出此时∠COD的度数为▲ °24. 已知m,n,t是有理数,单项式﹣xny的次数为3,而且多项式(m+1)x2+mx﹣tx+n+2是关于x的一次多项式.(1)、分别求m,n的值,及t的取值范围;(2)、若关于x的一元一次方程(m+1)x2+mx﹣tx+n+2=0的解是x=3,求t的值;(3)、若(2)中关于x的一元一次方程的解是整数,求整数t的值.25. 如图,点A和点B在数轴上对应的数分别为a和b,且(a+2)2+|b﹣8|=0. (1)、线段AB的长为 ;(2)、点C在数轴上所对应的为x,且x是方程 的解,在线段AB上是否存在点D.使AD+BD=CD?若存在,请求出点D在数轴上所对应的数,若不存在,请说明理由;(3)、在(2)的条件下,线段AD和BC分别以6个单位长度/秒和5个单位长度/秒的速度同时向右运动,运动时间为t秒,点M为线段AD的中点,点N为线段BC的中点,若MN=5,求t的值.
(1)、线段AB的长为 ;(2)、点C在数轴上所对应的为x,且x是方程 的解,在线段AB上是否存在点D.使AD+BD=CD?若存在,请求出点D在数轴上所对应的数,若不存在,请说明理由;(3)、在(2)的条件下,线段AD和BC分别以6个单位长度/秒和5个单位长度/秒的速度同时向右运动,运动时间为t秒,点M为线段AD的中点,点N为线段BC的中点,若MN=5,求t的值.