四川省巴中市2021-2022学年七年级上学期期末数学试卷
试卷更新日期:2022-03-08 类型:期末考试
一、单选题
-
1. ﹣ 的倒数是( )A、 B、﹣ C、3 D、﹣32. 如图是由6个完全相同的小正方体组成的几何体,其俯视图为( )
 A、
A、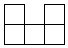 B、
B、 C、
C、 D、
D、 3. 下列各式中是一元一次方程的是( )A、x-3 B、x2-1=0 C、2x-3=0 D、x-y=34. 预防和控制新冠肺炎最有效的办法就是接种疫苗.截止2021年12月1日,某市累计接种新冠病毒疫苗超过350万剂次,用科学记数法表示350万为( )A、35×105 B、3.5×105 C、3.5×106 D、3.5×1075. 下列调查方式合适的是( )A、为了解市民对电影《我和我的祖国》的感受,小张在班上随机采访了8名学生 B、为了解“山东舰”航母舰载机的零部件的状况,检测人员用了普查的方式 C、为了解全国七年级学生视力情况,统计人员采用了普查的方式 D、为了解全校学生用于做数学作业的时间,小民同学在网上向3位好友做了调查6. 下列计算,结果正确的是( )A、4a2b﹣5ab2=﹣a2﹣b B、5a2+3a2=8a4 C、2x+3y=5xy D、3xy﹣5yx=﹣2xy7. 下列说法正确的是( )A、两点之间直线最短 B、线段MN就是M、N两点间的距离 C、射线AB和射线BA是同一条射线 D、将一根木条固定在墙上需要两枚钉子,其原理是两点确定一条直线8. 已知x=﹣2是方程2x+m﹣4=0的解,则m的值为( )A、8 B、﹣8 C、0 D、29. 如图1是一个小正方体的侧面展开图,小正方体从如图2所示的位置依次翻到第1格、第2格、第3格,这时小正方体朝上面的字是( )
3. 下列各式中是一元一次方程的是( )A、x-3 B、x2-1=0 C、2x-3=0 D、x-y=34. 预防和控制新冠肺炎最有效的办法就是接种疫苗.截止2021年12月1日,某市累计接种新冠病毒疫苗超过350万剂次,用科学记数法表示350万为( )A、35×105 B、3.5×105 C、3.5×106 D、3.5×1075. 下列调查方式合适的是( )A、为了解市民对电影《我和我的祖国》的感受,小张在班上随机采访了8名学生 B、为了解“山东舰”航母舰载机的零部件的状况,检测人员用了普查的方式 C、为了解全国七年级学生视力情况,统计人员采用了普查的方式 D、为了解全校学生用于做数学作业的时间,小民同学在网上向3位好友做了调查6. 下列计算,结果正确的是( )A、4a2b﹣5ab2=﹣a2﹣b B、5a2+3a2=8a4 C、2x+3y=5xy D、3xy﹣5yx=﹣2xy7. 下列说法正确的是( )A、两点之间直线最短 B、线段MN就是M、N两点间的距离 C、射线AB和射线BA是同一条射线 D、将一根木条固定在墙上需要两枚钉子,其原理是两点确定一条直线8. 已知x=﹣2是方程2x+m﹣4=0的解,则m的值为( )A、8 B、﹣8 C、0 D、29. 如图1是一个小正方体的侧面展开图,小正方体从如图2所示的位置依次翻到第1格、第2格、第3格,这时小正方体朝上面的字是( ) A、祝 B、你 C、成 D、功10. 如图,∠AOE=100°,∠BOF=80°,OE平分∠BOC,OF平分∠AOC,则∠EOF的度数为( )
A、祝 B、你 C、成 D、功10. 如图,∠AOE=100°,∠BOF=80°,OE平分∠BOC,OF平分∠AOC,则∠EOF的度数为( )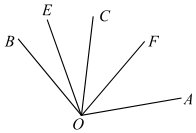 A、40° B、50° C、60° D、70°11. 某件商品,按成本价提高40%后标价,又以8折优惠卖出,结果仍可获利15元,则这件商品的成本价为( )A、115元 B、120元 C、125元 D、150元12. 如图,已知B,C两点把线段AD从左至右依次分成2:4:3三部分,M是AD的中点,BM=5cm,则线段MC的长为( )
A、40° B、50° C、60° D、70°11. 某件商品,按成本价提高40%后标价,又以8折优惠卖出,结果仍可获利15元,则这件商品的成本价为( )A、115元 B、120元 C、125元 D、150元12. 如图,已知B,C两点把线段AD从左至右依次分成2:4:3三部分,M是AD的中点,BM=5cm,则线段MC的长为( )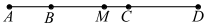 A、1cm B、2cm C、3cm D、4cm
A、1cm B、2cm C、3cm D、4cm二、填空题
-
13. 11°27′=°.14. 若3amb5与4a2bn+1是同类项,则m+n=.15. 如果代数﹣2y2+y﹣1的值为10,那么代数式4y2﹣2y+5的值为 .16. 已知a,b均为有理数,现我们定义一种新的运算,规定:a#b=a2+ab﹣5,例如:1#2=12+1×2﹣5=﹣2,则(﹣3)#6的值是 .17. 如图,3个平衡的天平左盘中“〇”、“□”分别表示两种质量不同的物体,则第三个天平右盘中砝码的质量为.
 18. 如图所示的几何体都是由棱长为1个单位的正方体摆成的,经计算可得第①个几何体的表面积为6个平方单位,第②个几何体的表面积为18个平方单位,第③个几何体的表面积是36个平方单位,…依此规律,则第⑩个几何体的表面积是个平方单位.
18. 如图所示的几何体都是由棱长为1个单位的正方体摆成的,经计算可得第①个几何体的表面积为6个平方单位,第②个几何体的表面积为18个平方单位,第③个几何体的表面积是36个平方单位,…依此规律,则第⑩个几何体的表面积是个平方单位.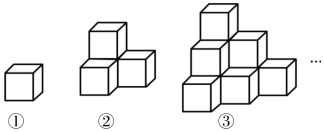
三、解答题
-
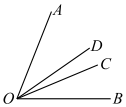
19. 计算与解方程:(1)、 ;(2)、 ;(3)、4x﹣3(20﹣x)+4=0;(4)、 .20. 先化简,再求值.已知代数式2(3x2﹣x+2y﹣xy)﹣3(2x2﹣3x﹣y+xy),其中x+y= ,xy=﹣2.21. 如图,∠AOC与∠BOC的度数比为5:2,OD平分∠AOB,若∠COD=15°,求∠AOB的度数.
 22. 抗洪救灾小组在甲地段有28人,乙地段有15人,现在又调来29人,分配在甲乙两个地段,要求调配后甲地段人数是乙地段人数的2倍,求应调至甲地段和乙地段各多少人?23. 某市为了解七年级数学教育教学情况,对全市七年级学生进行数学综合素质测评,我校也随机抽取了部分学生的测试成绩作为样本进行分析,请根据图中所给出的信息,解答下列问题:
22. 抗洪救灾小组在甲地段有28人,乙地段有15人,现在又调来29人,分配在甲乙两个地段,要求调配后甲地段人数是乙地段人数的2倍,求应调至甲地段和乙地段各多少人?23. 某市为了解七年级数学教育教学情况,对全市七年级学生进行数学综合素质测评,我校也随机抽取了部分学生的测试成绩作为样本进行分析,请根据图中所给出的信息,解答下列问题: (1)、在这次调查中被抽取学生的总人数为 ▲ 人;将表示成绩类别为“中”的条形统计图补充完整.(2)、成绩类别为“优”的圆心角的度数为.(3)、某校七年级共有750人参加了这次数学考试,估计本校七年级共有多少名学生的数学成绩可达到良或良以上等级?24. 已知方程(1﹣m2)x2﹣(m+1)x+8=0是关于x的一元一次方程.(1)、求m的值及方程的解.(2)、求代数式 的值.25. 如图,将一个边长为1的正方形纸片分割成7个部分,部分①的面积是边长为1的正方形纸片面积的一半,部分②的面积是部分①面积的一半,部分③的面积是部分②面积的一半,…依次类推.
(1)、在这次调查中被抽取学生的总人数为 ▲ 人;将表示成绩类别为“中”的条形统计图补充完整.(2)、成绩类别为“优”的圆心角的度数为.(3)、某校七年级共有750人参加了这次数学考试,估计本校七年级共有多少名学生的数学成绩可达到良或良以上等级?24. 已知方程(1﹣m2)x2﹣(m+1)x+8=0是关于x的一元一次方程.(1)、求m的值及方程的解.(2)、求代数式 的值.25. 如图,将一个边长为1的正方形纸片分割成7个部分,部分①的面积是边长为1的正方形纸片面积的一半,部分②的面积是部分①面积的一半,部分③的面积是部分②面积的一半,…依次类推. (1)、阴影部分的面积是;(2)、受此启发,试求 的值.26. 如图,数轴上点A,C对应的数分别为a,c,且.a,c满足|a+4|+(c﹣1)2022=0,点B对应的数为﹣3.
(1)、阴影部分的面积是;(2)、受此启发,试求 的值.26. 如图,数轴上点A,C对应的数分别为a,c,且.a,c满足|a+4|+(c﹣1)2022=0,点B对应的数为﹣3. (1)、求数a,c.(2)、点A,B沿数轴同时出发向右匀速运动,点A速度为2个单位长度/秒,点B速度为l个单位长度/秒,设运动时间为t秒,运动过程中,当A,B两点到原点O的距离相等时,求t的值.(3)、在(2)的条件下,点B运动到点C后立即以原速返回,到达自己的出发点后停止运动,点A运动至点C后也以原速返回,到达自己的出发点后又折返向点C运动,当点B停止运动时,点A随之停止运动,请直接写出在此运动过程中A,B两点同时到达的点在数轴上所表示的数.
(1)、求数a,c.(2)、点A,B沿数轴同时出发向右匀速运动,点A速度为2个单位长度/秒,点B速度为l个单位长度/秒,设运动时间为t秒,运动过程中,当A,B两点到原点O的距离相等时,求t的值.(3)、在(2)的条件下,点B运动到点C后立即以原速返回,到达自己的出发点后停止运动,点A运动至点C后也以原速返回,到达自己的出发点后又折返向点C运动,当点B停止运动时,点A随之停止运动,请直接写出在此运动过程中A,B两点同时到达的点在数轴上所表示的数.