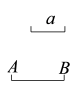贵州省遵义市2021-2022学年七年级上学期期末数学试卷
试卷更新日期:2022-03-08 类型:期末考试
一、单选题
-
1. 在-2.5,-2,0,1.5这几个数中,最小的数是( )A、-2.5 B、-2 C、0 D、1.52. 下列四个选项中,不是正方体展开图形的是( )A、
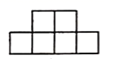 B、
B、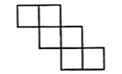 C、
C、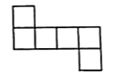 D、
D、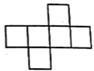 3. 下列计算正确的是( )A、 B、 C、 D、4. 若 是关于x的方程 的解,则m的值是( )A、1 B、-1 C、 D、5. 下列等式变形正确的是( )A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则6. 如图,将一块三角形木板截去一部分后,发现剩余木板的周长要比原三角形木板的周长大,能正确解释这一现象的数学知识是( )
3. 下列计算正确的是( )A、 B、 C、 D、4. 若 是关于x的方程 的解,则m的值是( )A、1 B、-1 C、 D、5. 下列等式变形正确的是( )A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则6. 如图,将一块三角形木板截去一部分后,发现剩余木板的周长要比原三角形木板的周长大,能正确解释这一现象的数学知识是( ) A、两直线相交只有一个交点 B、两点确定一条直线 C、经过一点有无数条直线 D、两点之间,线段最短7. 若 、 为有理数, , ,且 ,那么 , , , 的大小关系是( )A、 B、 C、 D、8. 解一元一次方程: ,下列去分母的过程正确的是( )A、2(2x-1)-x+2=1 B、(2x-1)-(x+2)=1 C、2(2x-1)-x+2=6 D、2(2x-1)-(x+2)=69. 如图,一副三角板(直角顶点重合)摆放在桌面上,若 ,则 等于( )
A、两直线相交只有一个交点 B、两点确定一条直线 C、经过一点有无数条直线 D、两点之间,线段最短7. 若 、 为有理数, , ,且 ,那么 , , , 的大小关系是( )A、 B、 C、 D、8. 解一元一次方程: ,下列去分母的过程正确的是( )A、2(2x-1)-x+2=1 B、(2x-1)-(x+2)=1 C、2(2x-1)-x+2=6 D、2(2x-1)-(x+2)=69. 如图,一副三角板(直角顶点重合)摆放在桌面上,若 ,则 等于( )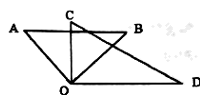 A、 B、 C、 D、10. 如果代数式 的值是5,那么 的值为( )A、-2 B、2 C、1 D、-311. 某商场把一个双肩包按进价提高30%标价,然后按八折出售,这样商场每卖出一个书包仍可盈利10元.设每个双肩书包的进价是x元,根据题意列一元一次方程正确的是( )A、 B、 C、 D、12. 在数轴上,点M、N分别表示数m,n.则点M、N之间的距离为 .已知点A,B,C,D在数轴上分别表示的数为a,b,c,d.且 ,则线段的长度为( )A、4.5 B、1.5 C、6.5或1.5 D、4.5或1.5
A、 B、 C、 D、10. 如果代数式 的值是5,那么 的值为( )A、-2 B、2 C、1 D、-311. 某商场把一个双肩包按进价提高30%标价,然后按八折出售,这样商场每卖出一个书包仍可盈利10元.设每个双肩书包的进价是x元,根据题意列一元一次方程正确的是( )A、 B、 C、 D、12. 在数轴上,点M、N分别表示数m,n.则点M、N之间的距离为 .已知点A,B,C,D在数轴上分别表示的数为a,b,c,d.且 ,则线段的长度为( )A、4.5 B、1.5 C、6.5或1.5 D、4.5或1.5二、填空题
-
13. 2021年贵州省禁毒微信订阅人数约48万人,将48万用科学记数法表示应为.14. 已知关于x,y的多项式 不含三次项,则a的值为.15. 有理数 , , 在数轴上所表示的点的位置如图所示,则化简 .
 16. 观察下列表格中的每组数,根据规律得出 的值为.
16. 观察下列表格中的每组数,根据规律得出 的值为.第一组数
6
8
10
第二组数
8
15
17
第三组数
10
24
26
第四组数
12
35
37
…
…
…
…
…
24
a
b
三、解答题
-
17. 计算(1)、(2)、18. 解下列方程(1)、(2)、19. 先化简,再求值: ,其中 .20. 某校七年级三个班级的学生在植树节当天义务植树.一班植树a棵,二班植树的棵数比一班的3倍少20棵,三班植树的棵数比二班的一半多15棵.(1)、求三个班共植树多少棵(用含 的式子表示);(2)、当 时,求二班比三班多植多少棵?21. 如图,在一个长方形休闲广场的四角都设计一块半径相同的四分之一圆形花坛,若圆的半径为 ,广场长为 ,宽为 .
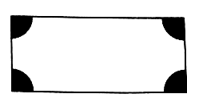 (1)、列式表示广场空地的面积;(2)、若广场的长为 ,宽为 ,圆形花坛的半径为 ,求广场空地的面积(计算结果保留 ).22. 如图,已知 平分 平分 .
(1)、列式表示广场空地的面积;(2)、若广场的长为 ,宽为 ,圆形花坛的半径为 ,求广场空地的面积(计算结果保留 ).22. 如图,已知 平分 平分 .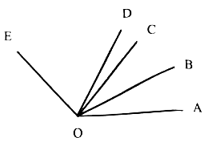 (1)、求 的度数.(2)、求 的度数.
(1)、求 的度数.(2)、求 的度数.