贵州省铜仁市石阡县2021-2022学年七年级上学期期末数学试卷

试卷更新日期：2022-03-08 类型：期末考试

进入出卷网下载

一、单选题

1. $- | - 2021 |$ 的相反数为（）

A、-2021 B、2021 C、 $- \frac{1}{2021}$ D、 $\frac{1}{2021}$

查看试题解析
2. 有理数 $a 、 b$ 在数轴上的位置如图所示，那么下列式子中成立的是（）

A、 $a < b$ B、 $a + b < 0$ C、 $a b > 0$ D、 $\frac{a}{b} > 0$

查看试题解析
3. 小明做了6道计算题：①﹣5﹣3＝﹣2；②0﹣（﹣1）＝1；③ $- 12 \div \frac{1}{2} = 24$ ；④3a﹣2a＝1；⑤3a²+2a²＝5a⁴；⑥3a²b﹣4ba²＝﹣a²b；请你帮他检查一下，他一共做对了（）

A、2题 B、3题 C、4题 D、5题

查看试题解析
4. 2020年12月8日，国家主席习近平同尼泊尔总统班达里互致信函，共同宣布珠穆朗的高度8848.86米，其中8848.86用科学记数法表示为（）

A、88.4886×10³ B、8.84886×10³ C、88.4886×10⁴ D、8.84886×10⁵

查看试题解析
5. 多项式 $2 x^{5} + 4 x y^{3} - 5 x^{2} - 1$ 的次数和常数项分别是（）

A、5，-1 B、5，1 C、10，-1 D、4，-1

查看试题解析
6. 把方程 $\frac{x}{3} - \frac{x + 1}{6} = 1$ 去分母，下列变形正确的是（）

A、 $2 x - (x + 1) = 1$ B、 $2 x - (x + 1) = 6$ C、 $2 x - x + 1 = 1$ D、 $2 x - x + 1 = 6$

查看试题解析
7. 一批上衣的进价为每件 $a$ 元，在进价的基础上提高50%后作为零售价，由于季节原因，打6折促销，则打折后每件上衣的价格为（）

A、 $a$ 元 B、 $0.9 a$ 元 C、 $0.92 a$ 元 D、 $1.04 a$ 元

查看试题解析
8. 如图，线段 $A D = 21 cm$ ，点 $B$ 在线段 $A D$ 上， $C$ 为 $B D$ 的中点，且 $A B = \frac{1}{3} C D$ ，则 $B C$ 的长度（）

A、 $6 cm$ B、 $7 cm$ C、 $8 cm$ D、 $9 cm$

查看试题解析
9. 每瓶A种饮料比每瓶B种饮料少 $1$ 元，小峰买了2瓶A种饮料和3瓶B种饮料，一共花了13元，如果设每瓶A种饮料为x元，那么下面所列方程正确的是（）

A、 $2 (x - 1) + 3 x = 13$ B、 $2 (x + 1) + 3 x = 13$ C、 $2 x + 3 (x + 1) = 13$ D、 $2 x + 3 (x - 1) = 13$

查看试题解析
10. 11点40分,时钟的时针与分针的夹角为（）

A、 140° B、130° C、120° D、110°

查看试题解析

二、填空题

11. 已知数轴上两点A，B它们所表示的数分别是＋4，－6，则线段AB＝

查看试题解析
12. 若两个单项式 $2 a^{2} b^{m - 1}$ 与 $n a^{2} b$ 的和为0，则 $m + n$ 的值是.

查看试题解析
13. 已知x＝1是方程3x﹣m＝x+2n的一个解，则整式m+2n+2020的值为.

查看试题解析
14. 若 ${(x - 3)}^{2} + | y + 5 | = 0$ ，则 $x y - y^{x} =$ .

查看试题解析
15. 已知∠1与∠2互余，∠2与∠3互补，若 $∠ 1 ＝ 33 ° 2 7^{'}$ ，则∠3＝.

查看试题解析
16. 根据下图所示的程序计算，若输入x的值为1，则输出y的值为．

查看试题解析

三、解答题

17. 计算：

(1)、 $- 3^{2} - (- 8) \times {(- 1)}^{5} \div {(- 1)}^{4}$ ；

(2)、 $- 1^{2} + {(- 1 \frac{1}{2})}^{3} \div \frac{3}{4} - | 0.25 - \frac{3}{8} |$

(3)、 $(\frac{2}{3} - \frac{3}{4} + \frac{1}{6}) \div (- \frac{1}{24})$

查看试题解析
18. 化简求值：

(1)、 $- (x^{2} - 3) - (7 - 5 x^{2})$ ，其中 $x = - 2$

(2)、 $4 (2 x^{2} y - x y^{2}) - 5 (x y^{2} + 2 x^{2} y)$ ，其中 $x = - \frac{1}{2} ， y = \frac{1}{3}$ .

查看试题解析
19. 解方程：

(1)、 $3 (2 x - 1) = 3 x + 1$ .

(2)、 $\frac{x - 10}{3} = \frac{1}{4} x - \frac{2}{3}$ .

查看试题解析
20. 方程 $2 (1 - x) = x - 1$ 的解与方程 $\frac{x - m}{3} = 2 x + m$ 的解相同，求 $m$ 的值.

查看试题解析
21. 某校随机抽取九年级部分同学接受一次内容为“最适合自己的考前减压方式”的调查活动，学校收集并整理数据后，将减压方式分为五类，并绘制了图1、图2两个不完整的统计图.请根据图中的信息解答下列问题：

(1)、求该校九年级接受调查的人数并补全条形统计图.

(2)、计算扇形统计图中的“体育活动”所对应的圆心角度数.

(3)、若该校九年级有450名学生，请估计该校九年级学生中喜欢“听音乐”方式进行考前减压的人数.

查看试题解析
22. 如图1，将一副直角三角板的两顶点重合叠放于点 $O$ ，其中一个三角板的顶点 $C$ 落在另一个三角板的边 $O A$ 上.已知 $∠ A B O = ∠ D C O = 90^{\circ}$ ， $∠ A O B = 45^{\circ}$ ， $∠ C O D = 60^{\circ}$ ，作 $∠ A O D$ 的平分线交边 $C D$ 于点 $E$ .

(1)、求 $∠ B O E$ 的度数；

(2)、如图2，若点 $C$ 不落在边 $O A$ 上，当 $∠ C O E = 15^{\circ}$ 时，求 $∠ B O D$ 的度数.

查看试题解析
23. 一艘轮船航行于甲、乙两地之间，顺水用3小时，逆水比顺水多用30分钟，已知轮船在静水中速度是每小时26千米，求水流速度.

查看试题解析
24. 如图1，已知点C在线段AB上，线段AC＝10厘米，BC＝6厘米，点M，N分别是AC，BC的中点.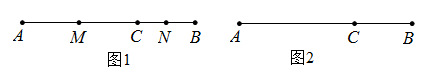

(1)、求线段MN的长度.

(2)、根据第（1）题的计算过程和结果，设AC＝a，BC＝b，其他条件不变，求MN的长度.

(3)、动点P、Q分别从A、B同时出发，点P以2cm/s的速度沿AB向右运动，终点为B，点Q以1cm/s的速度沿AB向左运动，终点为A，当一个点到达终点，另一个点也随之停止运动.设点P的运动时间为t（s）.当C、P、Q三点中，有一点恰好是以另外两点为端点的线段的中点时，直接写出时间t.

查看试题解析