福建省三明市尤溪县2021-2022学年九年级下学期开学考试数学试卷
试卷更新日期:2022-03-07 类型:开学考试
一、选择题:本题共10小题,每小题4分,共40分。
-
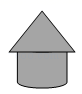
1. 如图,粮仓可以近似地看作由圆锥和圆柱组成,其主视图是( )
 A、
A、 B、
B、 C、
C、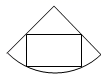 D、
D、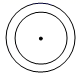 2. 若3x=4y,则下列结论一定成立的是( )A、 = B、 = C、 = D、 =3. 如图,平行于正多边形一边的直线把正多边形分割成两部分,则阴影部分多边形与原多边形相似的是( )A、
2. 若3x=4y,则下列结论一定成立的是( )A、 = B、 = C、 = D、 =3. 如图,平行于正多边形一边的直线把正多边形分割成两部分,则阴影部分多边形与原多边形相似的是( )A、 B、
B、 C、
C、 D、
D、 4. 下列一元二次方程中,有两个相等实数根的是( )A、 + 2 = 0 B、 = 2x C、( - 1)( - 2) = 0 D、 = 05. 在菱形ABCD中,对角线AC与BD相交于点O,添加以下条件,能判定菱形ABCD是正方形的是( )
4. 下列一元二次方程中,有两个相等实数根的是( )A、 + 2 = 0 B、 = 2x C、( - 1)( - 2) = 0 D、 = 05. 在菱形ABCD中,对角线AC与BD相交于点O,添加以下条件,能判定菱形ABCD是正方形的是( ) A、AB = AC B、OA = OC C、BC⊥CD D、AC⊥BD6. 把抛物线y=2x2向下平移1个单位,则平移后抛物线的解析式为( )A、y=2x2 + 1 B、y=2x2-1 C、y= D、y=7. 工人师傅在做矩形门窗时,不仅要测量两组对边的长度是否分别相等,还要测量它们的两条对角线是否相等,以确定门窗是否为矩形.这样做的依据是( )A、矩形的两组对边分别相等 B、矩形的两条对角线相等 C、有一个角是直角的平行四边形是矩形 D、对角线相等的平行四边形是矩形8. 如图,在直角坐标系中,△OAB的顶点为O(0,0),A(4,3),B(3,0).以点O为位似中心,在第三象限内作与△OAB的位似比为 的位似图形△OCD,则点C坐标( )
A、AB = AC B、OA = OC C、BC⊥CD D、AC⊥BD6. 把抛物线y=2x2向下平移1个单位,则平移后抛物线的解析式为( )A、y=2x2 + 1 B、y=2x2-1 C、y= D、y=7. 工人师傅在做矩形门窗时,不仅要测量两组对边的长度是否分别相等,还要测量它们的两条对角线是否相等,以确定门窗是否为矩形.这样做的依据是( )A、矩形的两组对边分别相等 B、矩形的两条对角线相等 C、有一个角是直角的平行四边形是矩形 D、对角线相等的平行四边形是矩形8. 如图,在直角坐标系中,△OAB的顶点为O(0,0),A(4,3),B(3,0).以点O为位似中心,在第三象限内作与△OAB的位似比为 的位似图形△OCD,则点C坐标( )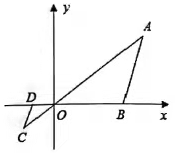 A、(- ,-1) B、(-1,- ) C、(-1,-1) D、(-2,-1)9. 点A(m,n)在二次函数y= -4的图象上,则2M-n的最大值是( )A、-5 B、-4 C、4 D、510. 如图,菱形ABCD的顶点分别在反比例函数y = 和y= 的图象上,若∠BCD=60°,则 的值是( )
A、(- ,-1) B、(-1,- ) C、(-1,-1) D、(-2,-1)9. 点A(m,n)在二次函数y= -4的图象上,则2M-n的最大值是( )A、-5 B、-4 C、4 D、510. 如图,菱形ABCD的顶点分别在反比例函数y = 和y= 的图象上,若∠BCD=60°,则 的值是( ) A、- B、- C、- D、-
A、- B、- C、- D、-二、填空题:本题共6小题,每小题4分,共24分.
-
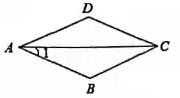
11. 如图,在菱形ABCD中,∠D=140°,则∠1=度.
 12. 若关于x的一元二次方程 = c没有实数根,则c的值可以是.(写出一个即可)13. 两个相似多边形的周长比是2:3,其中较小多边形的面积为12 ,则较大多边形的面积为 .14. 某篮球运动员进行定点投篮训练,其成绩如下表:
12. 若关于x的一元二次方程 = c没有实数根,则c的值可以是.(写出一个即可)13. 两个相似多边形的周长比是2:3,其中较小多边形的面积为12 ,则较大多边形的面积为 .14. 某篮球运动员进行定点投篮训练,其成绩如下表:投篮次数
10
100
10000
投中次数
9
89
9012
则这名运动员定点投篮一次,投中的概率约是(精确到0.1)
15. 已知抛物线y= + bx + 4经过(-2,n)和(4,n)两点,则b的值为.16. 如图,正方形ABCD中,点F是BC边上一点,连接AF,以AF为对角线作正方形AEFG,边FG与AC相交于点H,连接DG,以下四个结论: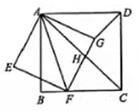
①∠EAB=∠BFE=∠DAG;
②△ACF∽△ADG;
③AH﹒AC = A ;
④DG⊥AC .
其中正确的是.(写出所有正确结论的序号)
三、解答题:本题共9小题,共86分,解答应写出文字说明、证明过程或演算步骤.
-
17. 解方程: + 4x - 5 = 0.18. 如图是两根木杆及其影子的图形.
 (1)、这个图形反映的是中心投影还是平行投影?答:(2)、请你在图中画出表示小树影长的线段AB.19. 已知某品牌蓄电池的电压为定值,使用该蓄电池作为电源时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.
(1)、这个图形反映的是中心投影还是平行投影?答:(2)、请你在图中画出表示小树影长的线段AB.19. 已知某品牌蓄电池的电压为定值,使用该蓄电池作为电源时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.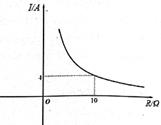 (1)、求这个反比例函数的表达式;(2)、如果以此蓄电池为电源的用电器的电流不能超过8A,那么该用电器的可变电阻至少是多少?20. 2022年冬奥会在我国北京和张家口举行,如图所示为冬奥会和冬残会的会徽“冬梦”“飞跃”,吉祥物“冰墩墩”“雪容融”,将四张正面分别印有以上4个图案的卡片(卡片的形状、大小、质地都相同)背面朝上洗匀.
(1)、求这个反比例函数的表达式;(2)、如果以此蓄电池为电源的用电器的电流不能超过8A,那么该用电器的可变电阻至少是多少?20. 2022年冬奥会在我国北京和张家口举行,如图所示为冬奥会和冬残会的会徽“冬梦”“飞跃”,吉祥物“冰墩墩”“雪容融”,将四张正面分别印有以上4个图案的卡片(卡片的形状、大小、质地都相同)背面朝上洗匀. (1)、若从中随机抽取一张卡片,则抽取的卡片上的图案恰好为吉样物“冰墩墩”的概率是;(2)、若从中一次同时随机抽取两张卡片,请用画树状图或列表的方法,求抽取的两张卡片上的图案正好一张是会徽另一张是吉祥物的概率.21. 如图,在△ABC中,D是AB边上一点,且BD=2DA.
(1)、若从中随机抽取一张卡片,则抽取的卡片上的图案恰好为吉样物“冰墩墩”的概率是;(2)、若从中一次同时随机抽取两张卡片,请用画树状图或列表的方法,求抽取的两张卡片上的图案正好一张是会徽另一张是吉祥物的概率.21. 如图,在△ABC中,D是AB边上一点,且BD=2DA.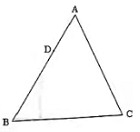 (1)、在AC边上求作点E,使CE=2EA;(要求:尺规作图,不写作法,保留作图痕迹)(2)、在(1)的条件下,若BC=12,求DE的长,22. 在菱形ABCD中,∠BAD = 60°,点E、F分别在边AB、AD上,且AE = DF,BF与DE交于点G.
(1)、在AC边上求作点E,使CE=2EA;(要求:尺规作图,不写作法,保留作图痕迹)(2)、在(1)的条件下,若BC=12,求DE的长,22. 在菱形ABCD中,∠BAD = 60°,点E、F分别在边AB、AD上,且AE = DF,BF与DE交于点G.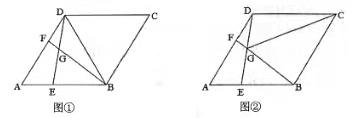 (1)、如图①,连接BD. 求证:△ADE ≌ △DBF;(2)、如图②,连接CG. 求证:BG + DG = CG.23. 2021年是我国脱贫胜利年,我国在扶贫方面取得了巨大的成就,技术扶贫也使得某县的一个电子器件厂扭亏为盈.该电子器件厂生产一种电脑显卡,2019年该类电脑显卡的成本是200元/个,2020年与2021年连续两年在技术扶贫的帮助下改进技术,降低成本,2021年该电脑显卡的成本降低到162元/个.(1)、若这两年此类电脑显卡成本下降的百分率相同,求平均每年下降的百分率;(2)、2021年某商场以高于成本价10%的价格购进若干个此类电脑显卡,以216.2元/个销售时,平均每天可销售20个,为了减少库存,商场决定降价销售. 经调查发现,单价每降低5元,每天可多售出10个,如果每天盈利1120元,单价应降低多少元?24. 在矩形ABCD中,AB = 6,AD = 4,点M为AB边上一个动点,连接DM,过点M作MN⊥DM,且MN = DM,连接DN.
(1)、如图①,连接BD. 求证:△ADE ≌ △DBF;(2)、如图②,连接CG. 求证:BG + DG = CG.23. 2021年是我国脱贫胜利年,我国在扶贫方面取得了巨大的成就,技术扶贫也使得某县的一个电子器件厂扭亏为盈.该电子器件厂生产一种电脑显卡,2019年该类电脑显卡的成本是200元/个,2020年与2021年连续两年在技术扶贫的帮助下改进技术,降低成本,2021年该电脑显卡的成本降低到162元/个.(1)、若这两年此类电脑显卡成本下降的百分率相同,求平均每年下降的百分率;(2)、2021年某商场以高于成本价10%的价格购进若干个此类电脑显卡,以216.2元/个销售时,平均每天可销售20个,为了减少库存,商场决定降价销售. 经调查发现,单价每降低5元,每天可多售出10个,如果每天盈利1120元,单价应降低多少元?24. 在矩形ABCD中,AB = 6,AD = 4,点M为AB边上一个动点,连接DM,过点M作MN⊥DM,且MN = DM,连接DN.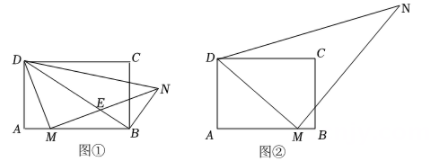 (1)、如图①,连接BD与BN,BD交MN于点E.
(1)、如图①,连接BD与BN,BD交MN于点E.①求证:△ABD∽△MND;
②求证:∠CBN=∠DNM;
(2)、如图②,当AM=4BM时,求证:A,C,N三点在同一条直线上.25. 平面直角坐标系中,抛物线y = - +2ax + 1 - a(a为常数)的顶点为A.(1)、当抛物线经过点(1,2),求抛物线的函数表达式;(2)、求顶点A的坐标(用含字母ɑ的代数式表示),判断顶点A在x轴的上方还是下方,并说明理由;(3)、当x ≥0时,抛物线y = - + 2ɑx + 1 - ɑ(ɑ为常数)的最高点到直线y = 3ɑ的距离为5,求ɑ的值.