广东省汕头市龙湖区2021年中考数学一模试卷
试卷更新日期:2022-03-07 类型:中考模拟
一、单选题
-
1. 下列数是无理数的是( )A、 B、 C、 D、02. 下列运算正确的是( )A、 B、 C、 D、3. 如图所示的几何体的左视图是( )
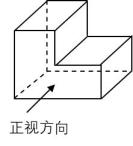 A、
A、 B、
B、 C、
C、 D、
D、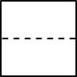 4. 函数y= 中自变量x的取值范围在数轴上表示正确的是( )A、
4. 函数y= 中自变量x的取值范围在数轴上表示正确的是( )A、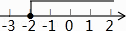 B、
B、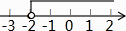 C、
C、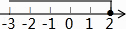 D、
D、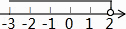 5. 教育部规定,初中生每天的睡眠时间不少于9个小时.小欣同学记录了她一周的睡眠时间,并将统计结果绘制成如图所示的折线统计图,则小欣这一周的睡眠不少于9个小时的有( )
5. 教育部规定,初中生每天的睡眠时间不少于9个小时.小欣同学记录了她一周的睡眠时间,并将统计结果绘制成如图所示的折线统计图,则小欣这一周的睡眠不少于9个小时的有( )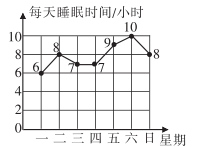 A、4天 B、3天 C、2天 D、1天6. 已知正比例函数与一次函数的图象交于点 , 则k的值为( )A、-2 B、-1 C、2 D、17. 如图,⊙O中,半径OC⊥弦AB于点D,点E在⊙O上,∠E=22.5°,AB=8,则半径OB等于( )
A、4天 B、3天 C、2天 D、1天6. 已知正比例函数与一次函数的图象交于点 , 则k的值为( )A、-2 B、-1 C、2 D、17. 如图,⊙O中,半径OC⊥弦AB于点D,点E在⊙O上,∠E=22.5°,AB=8,则半径OB等于( )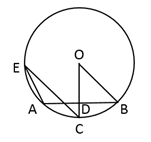 A、 B、 C、4 D、58. 在平面直角坐标系中,已知点A(﹣4,2),B(﹣6,﹣4),以原点O为位似中心,相似比为 , 把△ABO缩小,则点A的对应点A′的坐标是( )A、(﹣2,1) B、(﹣8,4) C、(﹣8,4)或(8,﹣4) D、(﹣2,1)或(2,﹣1)9. 如图,反比例函数和中,作直线 , 分别交x轴,和于点P,点A,点B,若 , 则( )
A、 B、 C、4 D、58. 在平面直角坐标系中,已知点A(﹣4,2),B(﹣6,﹣4),以原点O为位似中心,相似比为 , 把△ABO缩小,则点A的对应点A′的坐标是( )A、(﹣2,1) B、(﹣8,4) C、(﹣8,4)或(8,﹣4) D、(﹣2,1)或(2,﹣1)9. 如图,反比例函数和中,作直线 , 分别交x轴,和于点P,点A,点B,若 , 则( )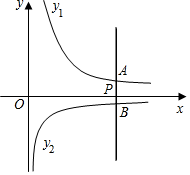 A、 B、3 C、-3 D、10. 如图,点P是边长为 的正方形ABCD的对角线BD上的动点,过点P分别作PE⊥BC于点E,PF⊥DC于点F,连接AP并延长,交射线BC于点H,交射线DC于点M,连接EF交AH于点G,当点P在BD上运动时(不包括B、D两点),以下结论中:①MF=MC;②AH⊥EF;③AP2=PM•PH;④EF的最小值是 .其中正确结论是( )
A、 B、3 C、-3 D、10. 如图,点P是边长为 的正方形ABCD的对角线BD上的动点,过点P分别作PE⊥BC于点E,PF⊥DC于点F,连接AP并延长,交射线BC于点H,交射线DC于点M,连接EF交AH于点G,当点P在BD上运动时(不包括B、D两点),以下结论中:①MF=MC;②AH⊥EF;③AP2=PM•PH;④EF的最小值是 .其中正确结论是( )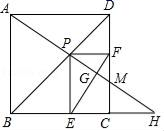 A、①③ B、②③ C、②③④ D、②④
A、①③ B、②③ C、②③④ D、②④二、填空题
-
11. 新型冠状病毒也叫2019-nCOV,该病毒比细胞小得多,大小约为(纳米),即为0.00000015米,约为一根头发丝直径的千分之一,数据0.00000015米用科学记数法表示为米.12. 点 关于y轴的对称点Q的坐标为.13. 如图,直线 , 直线l与直线a,b分别相交于A,B两点,过点A作直线l的垂线交直线b于点C,若 , 则的度数为 .
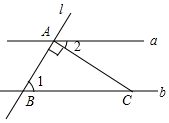 14. 实数a,b满足 , 则 .15. 如图,某堤坝的坝高为16米.如果迎水坡的坡度为 , 那么该大坝迎水坡的长度为米.
14. 实数a,b满足 , 则 .15. 如图,某堤坝的坝高为16米.如果迎水坡的坡度为 , 那么该大坝迎水坡的长度为米.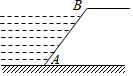 16. 如图,分别以等边三角形的三个顶点为圆心,以边长为半径画弧,得到的封闭图形叫作莱洛三角形,若 , 则莱洛三角形的面积(即阴影部分面积)为 .
16. 如图,分别以等边三角形的三个顶点为圆心,以边长为半径画弧,得到的封闭图形叫作莱洛三角形,若 , 则莱洛三角形的面积(即阴影部分面积)为 .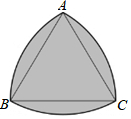 17. 如图,把矩形ABCD沿EF对折,使B与D重合,折痕EF交BD于G,连AG,若tan∠AGE= , BF=8,P为DG上一个动点,则PF+PC的最小值为 .
17. 如图,把矩形ABCD沿EF对折,使B与D重合,折痕EF交BD于G,连AG,若tan∠AGE= , BF=8,P为DG上一个动点,则PF+PC的最小值为 .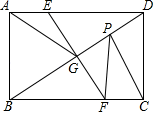
三、解答题
-
18. 先化简,再求值: ,其中 .19. 某新建火车站站前广场需要绿化的面积为35000米,施工队在绿化了11000米后,将每天的工作量增加为原来的1.5倍,结果提前4天完成了该项绿化工程.该项绿化工程原计划每天完成多少米?20. 如图,AD、BC相交于点O,AD=BC,∠C=∠D=90°.
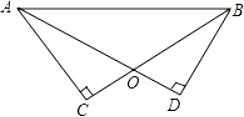 (1)、求证:△ACB≌△BDA;(2)、若∠ABC=32°,求∠CAO的度数.21. 如图,已知钝角△ABC.
(1)、求证:△ACB≌△BDA;(2)、若∠ABC=32°,求∠CAO的度数.21. 如图,已知钝角△ABC.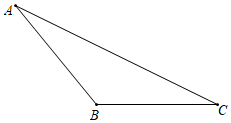 (1)、过钝角顶点B作BD⊥AC,交AC于点D(使用直尺和圆规,不写作法,保留作图痕迹);(2)、若BC=8,∠C=30°, , 求AB的长.22. 每年的6月8日是“世界海洋日”,某校决定在这一天开展系列海洋知识的宣传活动,活动有A.唱歌、B.舞蹈、C.绘画,D.演讲四项宣传方式.学校围绕“你最喜欢的宣传方式是什么?”在全校学生中进行随机抽样调查(四个选项中必选且只选一项),根据调查统计结果,给制了如下两种不完整的统计图表:
(1)、过钝角顶点B作BD⊥AC,交AC于点D(使用直尺和圆规,不写作法,保留作图痕迹);(2)、若BC=8,∠C=30°, , 求AB的长.22. 每年的6月8日是“世界海洋日”,某校决定在这一天开展系列海洋知识的宣传活动,活动有A.唱歌、B.舞蹈、C.绘画,D.演讲四项宣传方式.学校围绕“你最喜欢的宣传方式是什么?”在全校学生中进行随机抽样调查(四个选项中必选且只选一项),根据调查统计结果,给制了如下两种不完整的统计图表:选项
方式
百分比
A
唱歌
35%
B
舞蹈
a
C
绘画
25%
D
演讲
10%
请结合统计图表,回答下列问题:
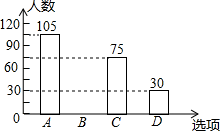 (1)、本次抽查的学生共人, , 并将条形统计图补充完整;(2)、如果该校学生有2000人,请你估计该校喜欢“唱歌”这项宣传方式的学生约有人.(直接在横线上填答案)(3)、学校采用抽签方式让每班在A、B、C、D四项宣传方式中随机抽取两项进行展示,请用树状图或列表法求某班所抽到的两项方式恰好是“唱歌”和“舞蹈”的概率.23. 在直角坐标系内的位置如图所示,反比例函数在第一象限内的图象与边交于点D(4,m),与AB边交于点 , 的面积为2.
(1)、本次抽查的学生共人, , 并将条形统计图补充完整;(2)、如果该校学生有2000人,请你估计该校喜欢“唱歌”这项宣传方式的学生约有人.(直接在横线上填答案)(3)、学校采用抽签方式让每班在A、B、C、D四项宣传方式中随机抽取两项进行展示,请用树状图或列表法求某班所抽到的两项方式恰好是“唱歌”和“舞蹈”的概率.23. 在直角坐标系内的位置如图所示,反比例函数在第一象限内的图象与边交于点D(4,m),与AB边交于点 , 的面积为2.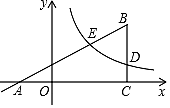 (1)、求m与n的数量关系;(2)、当时,求反比例函数的解析式和直线AB的解析式.24. 如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的直线交OP的延长线于点C,且CP=CB.
(1)、求m与n的数量关系;(2)、当时,求反比例函数的解析式和直线AB的解析式.24. 如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的直线交OP的延长线于点C,且CP=CB.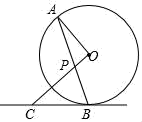 (1)、求证:BC是⊙O的切线;(2)、若OA=5,OP=3,求CB的长;(3)、设△AOP的面积是S1 , △BCP的面积是S2 , 且 .若⊙O的半径为4,BP= ,求tan∠CBP.25. 如图1,在平面直角坐标系xOy中,抛物线y=x2+k的顶点A在直线:y=x﹣3上,将抛物线沿直线向右上方平移,使其顶点P始终保持在直线上,设平移后的抛物线与原抛物线交于B点.
(1)、求证:BC是⊙O的切线;(2)、若OA=5,OP=3,求CB的长;(3)、设△AOP的面积是S1 , △BCP的面积是S2 , 且 .若⊙O的半径为4,BP= ,求tan∠CBP.25. 如图1,在平面直角坐标系xOy中,抛物线y=x2+k的顶点A在直线:y=x﹣3上,将抛物线沿直线向右上方平移,使其顶点P始终保持在直线上,设平移后的抛物线与原抛物线交于B点.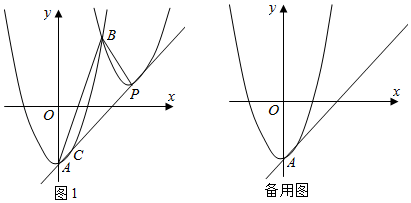 (1)、请直接写出k的值;(2)、若抛物线y=x2+k与直线:y=x﹣3的另一个交点为C.当点B与点C重合时.求平移后抛物线的解析式;(3)、连接AB,BP,当△ABP为直角三角形时,求出P点的坐标.
(1)、请直接写出k的值;(2)、若抛物线y=x2+k与直线:y=x﹣3的另一个交点为C.当点B与点C重合时.求平移后抛物线的解析式;(3)、连接AB,BP,当△ABP为直角三角形时,求出P点的坐标.