2021年山东省泰安市宁阳县中考数学二模试题
试卷更新日期:2022-03-07 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、-7 B、-9 C、9 D、2. 下列运算中,正确的是( )A、a2•a3=a5 B、2a﹣a=2 C、(a+b)2=a2+b2 D、2a+3b=5ab3. 一个几何体的三视图如图所示,则这个几何体是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 2020年6月23日,北斗三号最后一颗全球组网卫星在西昌卫星发射中心成功发射并顺利进入预定轨道,它的稳定运行标志着全球四大卫星导航系统之一的中国北斗卫星导航系统全面建成.该卫星距离地面约36000千米,将数据36000用科学记数法表示为( )A、 B、 C、 D、5. 某学校女子排球队12名队员的年龄分布如图所示,则这12名队员的年龄的众数、平均数分别是( )
4. 2020年6月23日,北斗三号最后一颗全球组网卫星在西昌卫星发射中心成功发射并顺利进入预定轨道,它的稳定运行标志着全球四大卫星导航系统之一的中国北斗卫星导航系统全面建成.该卫星距离地面约36000千米,将数据36000用科学记数法表示为( )A、 B、 C、 D、5. 某学校女子排球队12名队员的年龄分布如图所示,则这12名队员的年龄的众数、平均数分别是( ) A、15岁,15岁 B、15岁,14岁 C、14岁,14岁 D、14岁,15岁6. 如图,RtΔABC中,AB=9,BC=6,∠B=90°,将ΔABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为( )
A、15岁,15岁 B、15岁,14岁 C、14岁,14岁 D、14岁,15岁6. 如图,RtΔABC中,AB=9,BC=6,∠B=90°,将ΔABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为( ) A、 B、 C、4 D、57. 如图,⊙O是△ABC的外接圆,已知∠ACB=60°,则∠ABO的大小为( )
A、 B、 C、4 D、57. 如图,⊙O是△ABC的外接圆,已知∠ACB=60°,则∠ABO的大小为( ) A、30° B、40° C、45° D、50°8. 将一把直尺和一块含30°角的三角板ABC按如图所示的位置放置,如果∠CED=46°,那么∠BAF的度数为( )
A、30° B、40° C、45° D、50°8. 将一把直尺和一块含30°角的三角板ABC按如图所示的位置放置,如果∠CED=46°,那么∠BAF的度数为( ) A、48° B、16° C、14° D、32°9. 若关于x,y的方程组 的解满足 ,则m的最小整数解为( )A、﹣3 B、﹣2 C、﹣1 D、010. 直线与抛物线在同一坐标系中大致图象可能是( )A、
A、48° B、16° C、14° D、32°9. 若关于x,y的方程组 的解满足 ,则m的最小整数解为( )A、﹣3 B、﹣2 C、﹣1 D、010. 直线与抛物线在同一坐标系中大致图象可能是( )A、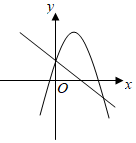 B、
B、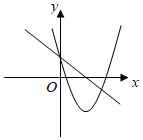 C、
C、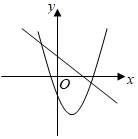 D、
D、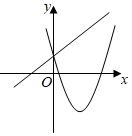 11. 二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,下列结论:①abc<0;②9a+3b+c<0;③a>;④若方程ax2+bx+c=0两个根x1和x2 , 则3<|x1﹣x2|<4,其中正确的结论有( )
11. 二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,下列结论:①abc<0;②9a+3b+c<0;③a>;④若方程ax2+bx+c=0两个根x1和x2 , 则3<|x1﹣x2|<4,其中正确的结论有( ) A、①②③ B、①②④ C、①③④ D、②③④12. 如图,动点在边长为2的正方形内,且 , 是边上的一个动点,是边的中点,则线段的最小值为( )
A、①②③ B、①②④ C、①③④ D、②③④12. 如图,动点在边长为2的正方形内,且 , 是边上的一个动点,是边的中点,则线段的最小值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 把多项式a3﹣6a2b+9ab2分解因式的结果是.14. 在直角坐标系中等腰直角三角形在如图所示的位置,点的横坐标为2,将绕点按逆时针方向旋转 , 得到△ , 则点的坐标为
 15. 如图,学校某数学兴趣小组想测量操场对面旗杆的高度,他们在点测得旗杆顶部的仰角为 , 再沿着坡度为的楼梯向下走了3.5米到达处,再继续向旗杆方向走了15米到达处在处测得旗杆顶部的仰角为 , 已知旗杆所在平台的高度为3.5米,则旗杆的高度为(结果精确到0.1,参考数据: , .
15. 如图,学校某数学兴趣小组想测量操场对面旗杆的高度,他们在点测得旗杆顶部的仰角为 , 再沿着坡度为的楼梯向下走了3.5米到达处,再继续向旗杆方向走了15米到达处在处测得旗杆顶部的仰角为 , 已知旗杆所在平台的高度为3.5米,则旗杆的高度为(结果精确到0.1,参考数据: , .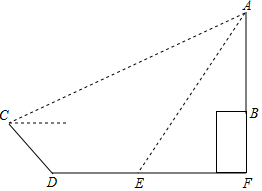 16. 如图,内接于 , 过点作直线 , 使 , 若是的中点,连接并延长交直线于点 , , , 则的半径是 .
16. 如图,内接于 , 过点作直线 , 使 , 若是的中点,连接并延长交直线于点 , , , 则的半径是 . 17. 如图,是半圆上一点,是直径,将弧沿翻折交于点 , 再将弧沿翻折交于点 , 若是弧的中点, , 则阴影部分面积为 .
17. 如图,是半圆上一点,是直径,将弧沿翻折交于点 , 再将弧沿翻折交于点 , 若是弧的中点, , 则阴影部分面积为 .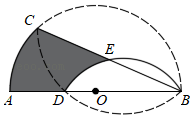 18. 如图,点 的坐标为 , 点 的坐标为 , 将 绕点 第一次顺时针旋转 得到△ , 将△ 绕点 第二次顺时针旋转 得到△ , 将△ 绕点 第三次顺时针旋转 得到△ , , 如此进行下去,则点 的坐标为 .
18. 如图,点 的坐标为 , 点 的坐标为 , 将 绕点 第一次顺时针旋转 得到△ , 将△ 绕点 第二次顺时针旋转 得到△ , 将△ 绕点 第三次顺时针旋转 得到△ , , 如此进行下去,则点 的坐标为 .
三、解答题
-
19. 先化简,再求代数式的值.其中a=2sin60°﹣3tan45°.20. 央视“经典咏流传”开播以来受到社会广泛关注.我市某校就“中华文化我传承——地方戏曲进校园”的喜爱情况进行了随机调查,对收集的信息进行统计,绘制了下面两副尚不完整的统计图.请你根据统计图所提供的信息解答下列问题:
图中A表示“很喜欢”,B表示“喜欢”,C表示“一般”,D表示“不喜欢”.
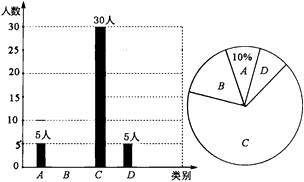 (1)、被调查的总人数是人,扇形统计图中C部分所对应的扇形圆心角的度数为.(2)、补全条形统计图;(3)、若该校共有学生1800人,请根据上述调查结果,估计该校学生中A类有人;(4)、在抽取的A类5人中,刚好有3个女生2个男生,从中随机抽取两个同学担任两角色,用树形图或列表法求出被抽到的两个学生性别相同的概率.21. 在平面直角坐标系中,O为坐标原点,点是直线上一点,直线交x轴于点C,直线与x轴交点 , 与y轴交于点B,直线、相交于点Q.
(1)、被调查的总人数是人,扇形统计图中C部分所对应的扇形圆心角的度数为.(2)、补全条形统计图;(3)、若该校共有学生1800人,请根据上述调查结果,估计该校学生中A类有人;(4)、在抽取的A类5人中,刚好有3个女生2个男生,从中随机抽取两个同学担任两角色,用树形图或列表法求出被抽到的两个学生性别相同的概率.21. 在平面直角坐标系中,O为坐标原点,点是直线上一点,直线交x轴于点C,直线与x轴交点 , 与y轴交于点B,直线、相交于点Q. (1)、 , 的解析式为 , 点Q坐标为;(2)、连接OP、OQ,直接写出的面积;(3)、在x轴上找一点M,使 , 则点M的坐标为 .22. 仙桃是遂宁市某地的特色时令水果.仙桃一上市,水果店的老板用2400元购进一批仙桃,很快售完;老板又用3700元购进第二批仙桃,所购件数是第一批的 倍,但进价比第一批每件多了5元.(1)、第一批仙桃每件进价是多少元?(2)、老板以每件225元的价格销售第二批仙桃,售出80%后,为了尽快售完,剩下的决定打折促销.要使得第二批仙桃的销售利润不少于440元,剩余的仙桃每件售价至少打几折?(利润=售价﹣进价)23. 在四边形中, , , 垂足为 .
(1)、 , 的解析式为 , 点Q坐标为;(2)、连接OP、OQ,直接写出的面积;(3)、在x轴上找一点M,使 , 则点M的坐标为 .22. 仙桃是遂宁市某地的特色时令水果.仙桃一上市,水果店的老板用2400元购进一批仙桃,很快售完;老板又用3700元购进第二批仙桃,所购件数是第一批的 倍,但进价比第一批每件多了5元.(1)、第一批仙桃每件进价是多少元?(2)、老板以每件225元的价格销售第二批仙桃,售出80%后,为了尽快售完,剩下的决定打折促销.要使得第二批仙桃的销售利润不少于440元,剩余的仙桃每件售价至少打几折?(利润=售价﹣进价)23. 在四边形中, , , 垂足为 . (1)、如图1,若 , 求证:;(2)、如图2,过点作 , 分别与 , 交于点 , , 点在边上,连接并延长,交于点 , 过作于 , , 且 .
(1)、如图1,若 , 求证:;(2)、如图2,过点作 , 分别与 , 交于点 , , 点在边上,连接并延长,交于点 , 过作于 , , 且 .①证明;
②若 , 探究与的数量关系.
24. 如图,抛物线经过点B(3,0),C(0,-2),直线L:交y轴于点E,且与抛物线交于A,D两点,P为抛物线上一动点(不与A重合).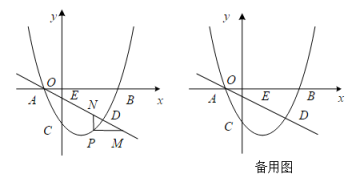 (1)、求抛物线的解析式.(2)、当点P在直线L下方时,过点P作PM∥x轴交L于点M,PN∥y轴交L于点N,求PM+PN的最大值.(3)、设F为直线L上的点,以E,C,P,F为顶点的四边形能否构成平行四边形?若能,求出点F的坐标;若不能,请说明理由.25. 如图
(1)、求抛物线的解析式.(2)、当点P在直线L下方时,过点P作PM∥x轴交L于点M,PN∥y轴交L于点N,求PM+PN的最大值.(3)、设F为直线L上的点,以E,C,P,F为顶点的四边形能否构成平行四边形?若能,求出点F的坐标;若不能,请说明理由.25. 如图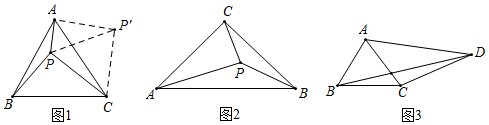 (1)、阅读理解
(1)、阅读理解利用旋转变换解决数学问题是一种常用的方法.如图1,点P是等边三角形ABC内一点,PA=1,PB= , PC=2.求∠BPC的度数.
为利用已知条件,不妨把△BPC绕点C顺时针旋转60°得△AP′C,连接PP′,则PP′的长为;在△PAP′中,易证∠PAP′=90°,且∠PP′A的度数为 , 综上可得∠BPC的度数为;
(2)、类比迁移如图2,点P是等腰Rt△ABC内的一点,∠ACB=90°,PA=2,PB= , PC=1,求∠APC的度数;
(3)、拓展应用如图3,在四边形ABCD中,BC=3,CD=5,AB=AC=AD.∠BAC=2∠ADC,请直接写出BD的长.