2021年山东省青岛市市北区中考数学一模试卷

试卷更新日期：2022-03-07 类型：中考模拟

进入出卷网下载

一、单选题

1. ﹣2021的相反数是（）

A、﹣2021 B、 $\frac{1}{2021}$ C、2021 D、﹣ $\frac{1}{2021}$

查看试题解析
2. 一个几何体的展开图如图所示，这个几何体是（）

A、三棱柱 B、三棱锥 C、四棱柱 D、四棱锥

查看试题解析
3. 5G 是第五代移动通信技术，5G网络理论下载速度可以达到每1300000KB 以上，这意味着下载一部高清电影只需要1秒．将1300000用科学记数法表示应为（）

A、13×10⁵ B、1.3×10⁵ C、1.3×10⁶ D、1.3×10⁷

查看试题解析
4. 下列图案中是轴对称图形的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 《孙子算经》中有一道题：“今有木，不知长短，引绳度之，余绳四尺五寸；屈绳量之，不足一尺，木长几何?”译文大致是：“用一根绳子去量一根木条，绳子剩余4.5尺；将绳子对折再量木条，木条剩余1尺，问木条长多少尺?”如果设木条长 $x$ 尺，绳子长 $y$ 尺，根据题意列方程组正确的是（）

A、 ${\begin{array}{l} x + 4.5 = y ， \\ \frac{y}{2} + 1 = x \end{array}$ B、 ${\begin{array}{l} x = y + 4.5 ， \\ \frac{y}{2} + 1 = x \end{array}$ C、 ${\begin{array}{l} x = y + 4.5 ， \\ y = \frac{x}{2} + 1 \end{array}$ D、 ${\begin{array}{l} x + 4.5 = y ， \\ x = \frac{y}{2} - 1 \end{array}$

查看试题解析
6. 如图，河坝横断面迎水坡AB的坡比为1： $\sqrt{2}$ ，坝高BC=4m，则AB的长度为（）

A、2 $\sqrt{6}$ m B、4 $\sqrt{2}$ m C、4 $\sqrt{3}$ m D、6m

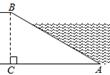查看试题解析
7. 若函数 $y = \frac{4}{x}$ 的图象与一次函数y＝kx＋2的图象有公共点，则k的取值范围是（）

A、k≥ $\frac{1}{4}$ B、k≥ $- \frac{1}{4}$ ，且k≠0 C、k≤ $\frac{1}{4}$ ，且k≠0 D、k≤ $- \frac{1}{4}$

查看试题解析
8. 如图，正方形ABCD中，E、F分别为BC、CD边上的点，∠EAF＝45°，则下列结论中正确的有（）
①BE+DF＝EF；②tan∠AMD＝ $\frac{C D}{D F}$ ；③BM²+DN²＝MN²；④若EF＝1.5，△AEF的面积是3，则正方形ABCD的面积是4．

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

9. 计算： $(\frac{1}{3})^{- 1} - (\sqrt{5} - 2)^{0}$ ＝．

查看试题解析
10. 儿童节期间，游乐场里有一种游戏的规则是：在一个装有6个红球和若干白球（每个球除颜色外，其它都相同）的袋中，随机摸一个球，摸到一个红球就得欢动世界通票一张，已知参加这种游戏的有300人，游乐场为此游戏发放欢动世界通票60张，请你通过计算估计袋中白球的数量是个．

查看试题解析
11. 一个n边形的内角和是它外角和的4倍，则n= ．

查看试题解析
12. 如图，反比例函数y＝ $\frac{k}{x}$ 的图象上有一点A，过点A作AB⊥x轴于B，S_△AOB＝2，则k＝．

查看试题解析
13. 如图，在扇形AOB中，∠AOB=90°，OA=4，以OB为直径作半圆，圆心为点C，过点C作OA的平行线分别交两弧点D、E，则阴影部分的面积为.

查看试题解析
14. 老师用10个1cm×1cm×1cm的小正方体摆出一个立体图形，它的主视图如图①所示，且图中任意两个相邻的小正方体至少有一条棱（1cm）共享，或有一面（1cm×1cm）共享．老师拿出一张3cm×4cm的方格纸（如图②），请小亮将此10个小正方体依主视图摆放在方格纸中的方格内，小亮摆放后的几何体表面积最大为 cm² ．（小正方体摆放时不得悬空，每一小正方体的棱均与水平线垂直或平行）

查看试题解析

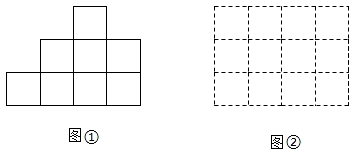
三、解答题

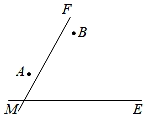
15. 青岛地铁8号线是青岛第六条建成运营的线路，地铁沿线的两个商场A、B与两条道路MF和ME的位置如图所示，其中ME是东西方向的道路，现需要修建一个地铁口（用点O表示），要求点O到两个商场A、B的距离相等，到两条道路MF和ME的距离也相等，且在∠FME的内部．请在示意图中作出一个符合条件的点O．

查看试题解析
16.

(1)、化简： $(1 - \frac{1}{x - 2}) \div \frac{x^{2} - 9}{x - 2}$ ；

(2)、若关于x的方程2x²+4x﹣c＝0有两个相等的实数根，求方程的解．

查看试题解析
17. 元旦联欢会上，明明和磊磊玩掷骰子的游戏．现有一枚均匀的正方体骰子，每个面上分别标上数字1、2、3、4、5、6．游戏规则是：明明和磊磊各掷一次骰子，若两次朝上的点数之和是3的倍数，则明明获胜，否则磊磊获胜．

(1)、用画树状图或列表的方法表示所有可能的结果；

(2)、你认为这个游戏规则对明明和磊磊公平吗？请说明理由．

查看试题解析
18. 近年来，无人机航拍测量的应用越来越广泛．如图，无人机从A处观测某建筑物至高点O时，俯角为37°；继续水平前行10米到达B处，观测点O，此时的俯角为45°，已知无人机的水平飞行高度为45米．求这栋楼的高度是多少米．(结果精确到0.1)(参考数据：sin37°≈0.60，cos37°≈0.79，tan37°≈0.75， $\sqrt{2}$ ≈1.41)

查看试题解析

19. 为贯彻《关于全面加强新时代大中小学劳动教育的意见》，各学校都在深入开展劳动教育.某校为了解七、八年级学生一学期参加课外劳动时间（单位：小时）的情况，从该校七、八年级中各随机抽查了20名学生进行问卷调查，并将调查结果进行整理，描述和分析（

A ： 0 \leq t < 20

，

B ： 20 \leq t < 40

，

C ： 40 \leq t < 60

，

D ： 60 \leq t < 80

，

E ： 80 \leq t < 100

），下面给出了部分信息.

七年级抽取的学生在C组的课外劳动时间为：40，40，50，55

八年级抽取的20名学生的课外劳动时间为：10，15，20，25，30，35，40，40，45，50，50，50，55，60，60，75，75，80，90，95

七年级抽取的学生的课外劳动时间的扇形统计图

七，八年级抽取的学生的课外劳动时间的统计量

年级	平均数	众数	中位数	方差
七年级	50	35	$a$	580
八年级	50	$b$	50	560

根据以上信息，解答下列问题：

(1)、直接写出

a

，

b

，

m

的值；

(2)、根据以上数据，在该校七、八年级中，你认为哪个年级参加课外劳动的情况较好？请说明理由（一条理由即可）；

(3)、若该校七、八年级分别有学生400人，试估计该校七、八年级学生一学期课外劳动时间不少于60小时的人数之和.

查看试题解析

20. 某古代石桥有17个大小相同的桥洞，桥面平直，其中三个桥洞图案如下左图所示．每个桥洞均可抽象成抛物线形状，其最大高度为4.5m，宽度为6m．将桥墩的宽度、厚度忽略不计，以水平方向为横轴，建立如下右图所示的平面直角坐标系，OM=6．

(1)、求OAM这条抛物线的函数关系式；

(2)、如图所示，若想在桥洞距水平面3米高的内壁处，安装照明灯，请计算两盏灯P、H之间的水平距离为多少米？

(3)、若想在每个桥洞距水平面3米高的内壁处都安装照明灯，则这三个桥洞最左端的灯与最右端灯P、Q之间的水平距离为米(请直接给出答案，无需提供求解过程)．

查看试题解析
21. 如图，已知四边形ABCD中，对角线AC，BD相交于点O，且OA＝OC，OB＝OD，过O点的线段EF，分别交AD，BC于点E，F．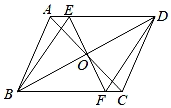

(1)、求证：△AOE≌△COF；

(2)、如果∠EBD＝∠CBD，请判断并证明四边形BEDF的形状．

查看试题解析
22. 六一前夕，某商场采购A、B两种品牌的卡通笔袋，已知每个A品牌笔袋的进价，比每个B品牌笔袋的进价多2元；若用3000元购进A品牌笔袋的数量，与用2400元购进B品牌笔袋的数量相同．

(1)、求每个A品牌笔袋和每个B品牌笔袋的进价分别是多少元；

(2)、该商场计划用不超过7220元采购A、B两种品牌的笔袋共800个，且其中B品牌笔袋的数量不超过400个，求该商场共有几种进货方式；

(3)、若每个A品牌笔袋售价16元，每个B品牌笔袋售价12元，在第（1）（2）问的前提下，不计其他因素，将所采购的A、B两种笔袋全部售出，求该商场可以获得的最大利润为多少元．

查看试题解析
23. 【学习方法】
数学中，常对同一个量（图形的面积、点的个数、三角形的内角和等）用两种不同的方法计算，从而建立相等关系，我们把这一思想称为“算两次”．“算两次”也称做富比尼原理，是一种重要的数学思想．
例如：
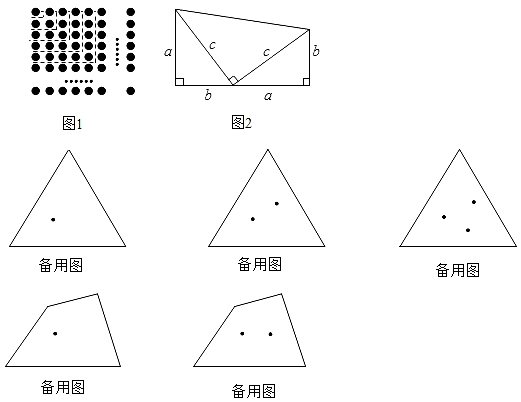
图1，将n行n列的棋子排成一个正方形，我们用两种不同的方法计算棋子的个数：
算法Ⅰ：
类比正方形面积的计算，图形可以看作n行棋子，每行都有n枚，因此棋子的总数是：
n×n＝n²
算法Ⅱ：
沿虚线将图案分割，可以发现：
第一层虚线内有1枚棋子，
第二层虚线内有3枚棋子，
第三层虚线内有5枚棋子…
第n层虚线内有（2n﹣1）枚棋子，
则棋子总数为1+3+5+7+…+2n﹣1
由此可得：1+3+5+7+…+2n﹣1＝n²

(1)、【类比尝试】
如图2，两个边长分别为a、b、c的直角三角形和一个两条直角边都是c的直角三角形拼成一个梯形．请用两种不同的方法计算梯形的面积，并写出你发现的结论．
算法Ⅰ：
算法Ⅱ：
你发现的结论是．
经过整理，这个结论恰好可以证明我们学过的重要定理．

(2)、【拓展探究】
富比尼原理给我们重要的启发：
从同一个问题的不同角度展开探究，往往会有惊喜地发现．
问题：
n边形有n个顶点，在它的内部再画m个点，以这（m+n）个点为顶点，把n边形剪成若干个三角形，设最多可以剪得y个这样的三角形．可以用含m、n的代数式表示y吗？
问题探究：
为了解决这个问题，我们先从简单的情况入手：
（一）研究最简单的多边形﹣﹣三角形．
三角形有3个顶点，在它的内部再画m个点，把三角形剪成若干个三角形，设最多可以剪得y个这样的三角形，那么可以用含有m的代数式来表示y吗？
方法Ⅰ：关注要素﹣﹣三角形内部每增加一个点，与最多可以剪得多少个三角形之间的关系．
从n＝3，m＝1开始研究：
当n＝3，m＝1时，最多可以把原三角形剪成3个三角形；
当n＝3，m＝2时，最多可以把原三角形剪成（3+2）个三角形；
当n＝3，m＝3时，最多可以把原三角形剪成（5+2）个三角形；
…
进行从特殊到一般的归纳：
对于一般的情形，在三角形内画m个点，第一个点将三角形分成了3个三角形，三角形内部每增加一个点，可增加个三角形．
故n＝3时，用含有m的代数式表示y＝；
方法Ⅱ：关注要素﹣﹣顶点数对组成三角形的作用．
三角形的三个顶点和它内部的1个点，共4个点，以这4个点为顶点，最多可以组成3个互不重叠的小三角形．
三角形的三个顶点和它内部的2个点，共5个点，以这5个点为顶点，最多可以组成5个互不重叠的小三角形．
三角形的三个顶点和它内部的3个点，共6个点，以这6个点为顶点，最多可以组成7个互不重叠的小三角形．
…
进行从特殊到一般的归纳：
三角形的三个顶点和它内部的m个点，共（m+3）个点，以这（m+3）个点为顶点，最多可以组成个互不重叠的小三角形．
以三角形的三个顶点和它内部的m个点，可把三角形最多剪成个互不重叠的小三角形．
（二）在四边形中研究类似的问题．
四边形有4个顶点，在它的内部再画m个点，把四边形剪成若干个三角形，设最多可以剪得y个三角形，那么可以用含有m的代数式来表示y吗？
方法Ⅰ：
对于一般的情形，在四边形内画m个点，第一个点将四边形分成了4个三角形；四边形内部每增加一个点，可增加个三角形．
故n＝4时，用含有m的代数式来表示y：y＝．
方法Ⅱ：
四边形的四个顶点和它内部的m个点，共（m+4）个点，以这（m+4）个点为顶点，最多可以组成个互不重叠的小三角形．

(3)、问题解决：
对于一般的情形，在n边形内画m个点，通过多角度探究、归纳猜想和算两遍方法的验证，可得y＝（用含m、n的代数式表示）．

查看试题解析
24. 已知：如图，在矩形ABCD中，AB＝8cm，BC＝6cm．点P从点B出发，沿BC方向匀速运动，速度为1cm/s；点Q从点C出发，沿CD方向匀速运动，速度为2cm/s；点E从点D出发，沿DA方向匀速运动，速度为0.5cm/s；点P、Q、E同时出发．对角线AC的中点为O，连接AP、PQ、QE．设运动时间为t(s)(0＜t≤4)，解答下列问题：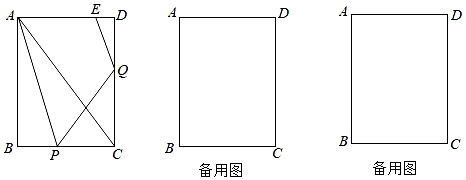

(1)、是否存在某一时刻t，使 $A P ∥ E Q$ ？若存在，求出t的值；若不存在，请说明理由．

(2)、连接OP、OE，设四边形OPQE的面积为y(cm²)，求y与t的函数关系式；

(3)、在直线AD上作点E关于CD的轴对称点F，是否存在某一时刻t，使P、Q、F三点共线？若存在，直接写出t的值(不需提供解答过程)；若不存在，请说明理由．

查看试题解析