2021年山东省临沂市沂水县中考数学一模试卷
试卷更新日期:2022-03-07 类型:中考模拟
一、单选题
-
1. 的绝对值是( )A、 B、 C、0 D、2. 下列选项是科学防控知识的图片,图片上有图案和文字说明,其中的图案是轴对称图形的是( )A、
 打喷嚏捂鼻子
B、
打喷嚏捂鼻子
B、 喷嚏后慎揉眼
C、
喷嚏后慎揉眼
C、 戴口罩讲卫生
D、
戴口罩讲卫生
D、 勤洗手勤通风
3. 在数轴上,点A,B在原点O的两侧,分别表示数a,1,将点A向右平移2个单位长度,得到点C,若CO=BO,则a的值为( )A、1 B、-1 C、-2 D、-34. 一个物体的三视图如图所示,其中主视图和左视图是全等的等边三角形,俯视图是圆,根据图中所示数据,可求这个物体的表面积为( )
勤洗手勤通风
3. 在数轴上,点A,B在原点O的两侧,分别表示数a,1,将点A向右平移2个单位长度,得到点C,若CO=BO,则a的值为( )A、1 B、-1 C、-2 D、-34. 一个物体的三视图如图所示,其中主视图和左视图是全等的等边三角形,俯视图是圆,根据图中所示数据,可求这个物体的表面积为( ) A、π B、2π C、3π D、( +1)π5. 如图,直线 , 点A在直线上,以点A为圆心,适当长为半径画弧,分别交直线于B,C两点,连接 , 若 , 则的度数为( )
A、π B、2π C、3π D、( +1)π5. 如图,直线 , 点A在直线上,以点A为圆心,适当长为半径画弧,分别交直线于B,C两点,连接 , 若 , 则的度数为( )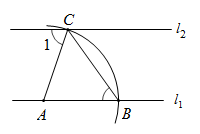 A、36° B、54° C、72° D、75°6. 下列运算正确的是( )A、(﹣2m3)2=4m6 B、m2•m3=m6 C、3m+m2=3m3 D、(m﹣n)2=m2﹣n27. 已知有等腰三角形两边长为一元二次方程x2-3x+2=0的两根,则等腰三角形周长是( )A、4 B、5 C、4或5 D、不能确定8. 某学习小组进行“用频率估计概率”的试验时,统计了某一结果出现的频率如下表,则符合这一结果的试验可能是( )
A、36° B、54° C、72° D、75°6. 下列运算正确的是( )A、(﹣2m3)2=4m6 B、m2•m3=m6 C、3m+m2=3m3 D、(m﹣n)2=m2﹣n27. 已知有等腰三角形两边长为一元二次方程x2-3x+2=0的两根,则等腰三角形周长是( )A、4 B、5 C、4或5 D、不能确定8. 某学习小组进行“用频率估计概率”的试验时,统计了某一结果出现的频率如下表,则符合这一结果的试验可能是( )试验次数
100
200
500
800
1000
1200
实验频率
0.343
0.326
0.335
0.330
0.331
0.330
A、先后两次抛掷一枚质地均匀的硬币,两次都是反面朝上 B、先后两次掷一枚质地均匀的骰子,两次的点数和不大于6 C、将一个篮球和一个足球随机放入三个不同的篮子中,恰有一个篮子为空 D、从两男两女四人中抽取两人参加朗读比赛,两人性别相同9. 我国古代数学著作《增删算法统宗》记载“绳索量牵”问题;“一条竿子一条索,索比竿子长一托.折回索子却量竿,却比竿子短一托.”其大意为:现有一根竿和一条绳索,用绳索去量竿,绳索比竿长1托;如果将绳索对半折后再去量竿,就比竿短1托.设绳索长x托,则正确的方程是( )A、2x=(x-1)-1 B、2x=(x+1)+1 C、x=(x+1)+1 D、x=(x-1)-110. 为了减轻学生课外作业负担,数学老师准备按照学生每天课外作业完成量(完成题目个数)实行分档布置作业.作业量分档递增,计划使第一档、第二档和第三档的作业量覆盖全校学生的70%,20%和10%,为合理确定各档之间的界限,随机抽查了该校500名学生过去一个阶段完成作业量的平均数(单位:个);绘制了统计图.如图所示,下面四个推断合理的是( )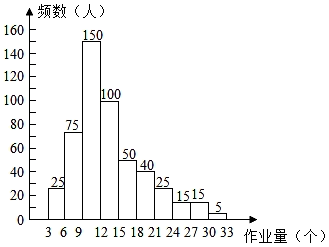 A、每天课外作业完成量不超过15个题的该校学生按第二档布置作业 B、每天课外作业完成量超过21个的该校学生按第三档布置作业 C、该校学生每天课外作业完成量的平均数不超过18 D、该校学生每天课外作业完成量的中位数在15﹣18之间11. 观察下列两行数:
A、每天课外作业完成量不超过15个题的该校学生按第二档布置作业 B、每天课外作业完成量超过21个的该校学生按第三档布置作业 C、该校学生每天课外作业完成量的平均数不超过18 D、该校学生每天课外作业完成量的中位数在15﹣18之间11. 观察下列两行数:0,2,4,6,8,10,12,14,16,…
0,3,6,9,12,15,18,21,24,…
探究发现:第1个相同的数是0,第2个相同的数是6,…,若第n个相同的数是102,则n等于( )
A、18 B、19 C、20 D、2112. 如图,在中,分别是边上的中线,于点O,点F是的中点,若 , 则的长是( )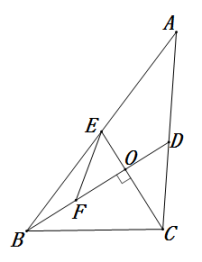 A、7 B、5 C、4 D、313. 若a2=b+2,b2=a+2,(a≠b)则a2﹣b2﹣2b+2的值为( )A、﹣1 B、0 C、1 D、314. 如图,点C , D在以AB为直径的⊙O上,且CD平分∠ACB , 若CD= ,∠CBA=15°,则AB的长是( )
A、7 B、5 C、4 D、313. 若a2=b+2,b2=a+2,(a≠b)则a2﹣b2﹣2b+2的值为( )A、﹣1 B、0 C、1 D、314. 如图,点C , D在以AB为直径的⊙O上,且CD平分∠ACB , 若CD= ,∠CBA=15°,则AB的长是( )
 A、 B、4 C、 D、
A、 B、4 C、 D、二、填空题
-
15. 不等式组 的解集为.16. 化简: ﹣ = .
17. 《九章算术》中记载了一种测量井深的方法.如图所示,在井口B处立一根垂直于井口的木杆BD,从木杆的顶端D观察水岸C,视线与井口的直径AB交于点E,如果测得米,米,米,那么井深为米.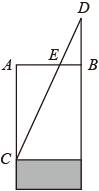 18. 如图,在中, , P为AB边上一动点,以为邻边作平行四边形 , 则对角线的最小值为 .
18. 如图,在中, , P为AB边上一动点,以为邻边作平行四边形 , 则对角线的最小值为 .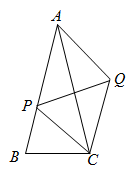
三、解答题
-
19. 定义:若两个函数的图象关于直线y=x对称,则称这两个函数互为反函数.请写出函数y=-2x+1的反函数的解析式 .20. 计算: .21. A,B两家酒店规模相当,去年下半年的月盈利折线统计图如图所示。
 (1)、要评价这两家酒店7~12月的月盈利的平均水平,你选择什么统计量?求出这个统计量。(2)、已知A,B两家酒店7~12月的月盈利的方差分别为1.073(平方万元),0.54(平方万元)。根据所给的方差和你在(1)中所求的统计量,结合折线统计图,你认为去年下半年哪家酒店经营状况较好?请简述理由。22. 如图,在树正东方向两个相距6m的A,B两点处,测得树顶端D的仰角为37°,45°,在树的正西方向的C处测得树顶端D的仰角是64°.求B,C之间的距离BC.(参考数据:sin64°≈0.90,cos64°≈0.44,tan64°≈2.0,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75.)
(1)、要评价这两家酒店7~12月的月盈利的平均水平,你选择什么统计量?求出这个统计量。(2)、已知A,B两家酒店7~12月的月盈利的方差分别为1.073(平方万元),0.54(平方万元)。根据所给的方差和你在(1)中所求的统计量,结合折线统计图,你认为去年下半年哪家酒店经营状况较好?请简述理由。22. 如图,在树正东方向两个相距6m的A,B两点处,测得树顶端D的仰角为37°,45°,在树的正西方向的C处测得树顶端D的仰角是64°.求B,C之间的距离BC.(参考数据:sin64°≈0.90,cos64°≈0.44,tan64°≈2.0,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75.)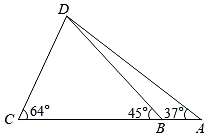 23. 汽车从甲地开往乙地,记汽车行驶时间为t小时,平均速度为v千米/小时(汽车行驶速度不超过100千米/小时).根据经验,v,t的一组对应值如下表:
23. 汽车从甲地开往乙地,记汽车行驶时间为t小时,平均速度为v千米/小时(汽车行驶速度不超过100千米/小时).根据经验,v,t的一组对应值如下表:v(千米/小时)
75
80
85
90
95
t(小时)
4.00
3.75
3.53
3.33
3.16
(1)、根据表中的数据,分析说明平均速度v(千米/小时)关于行驶时间t(小时)的函数关系,并求出其表达式;(2)、汽车上午8:00从甲地出发,能否在上午10:30之前到达乙地?请说明理由;(3)、若汽车到达乙地的行驶时间t满足3.5≤t≤4,求平均速度v的取值范围.24. 如图,AB是⊙O的直径,点C,点D在⊙O上,AC=CD,AD与BC相交于点E,点F在BC的延长线上,且AF=AE.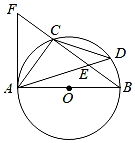 (1)、求证:AF是⊙O的切线;(2)、若EF=6,sin∠BAC= , 求⊙O的半径.25. 如图,抛物线y=x2+bx+c与x轴交于A,B两点(点A在点B左侧),与y轴交于点C(0,3).
(1)、求证:AF是⊙O的切线;(2)、若EF=6,sin∠BAC= , 求⊙O的半径.25. 如图,抛物线y=x2+bx+c与x轴交于A,B两点(点A在点B左侧),与y轴交于点C(0,3).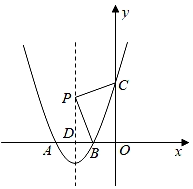 (1)、若抛物线的对称轴是直线x=-2.
(1)、若抛物线的对称轴是直线x=-2.①求抛物线的解析式;
②点P在对称轴上,若△PBC的面积是6,求点P的坐标;
(2)、当b≤0,﹣2≤x≤0时,函数y的最大值满足2≤y≤10,求b的取值范围.26. 如图1,点E为正方形ABCD内一点,∠AEB=90°,现将Rt△ABE绕点B按顺时针方向旋转90°,得到△CBF(点A的对应点为点C),延长AE交CF于点G.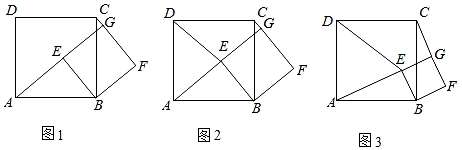 (1)、求证:四边形BEGF是正方形;(2)、连接DE,①如图2,若AB=15,CG=3,试求BE的长;②如图3,若DA=DE,求证:CG=FG.
(1)、求证:四边形BEGF是正方形;(2)、连接DE,①如图2,若AB=15,CG=3,试求BE的长;②如图3,若DA=DE,求证:CG=FG.