2021年山东省临沂市蒙阴县中考数学模拟试题
试卷更新日期:2022-03-07 类型:中考模拟
一、单选题
-
1. 下列实数中,是有理数的是( )A、 B、2.020020002 C、 D、 π2. 在下列运动图形的简笔画中,可以看作轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列计算不正确的个数是( )
3. 下列计算不正确的个数是( )① ② ③ ④ ⑤ .
A、2 B、3 C、4 D、54. 如图,若直线那么与之间的数量关系是( ) A、 B、 C、 D、5. 不等式组的解集为( )A、≤2 B、x>-1 C、-1<≤2 D、-1≤≤26. 如图,点在半径为的内, , 为上一点,延长、交于、当取最大值时,的长等于( )
A、 B、 C、 D、5. 不等式组的解集为( )A、≤2 B、x>-1 C、-1<≤2 D、-1≤≤26. 如图,点在半径为的内, , 为上一点,延长、交于、当取最大值时,的长等于( ) A、 B、 C、 D、7. 下列各式计算正确的是( )A、 B、 C、 D、8. 如图,圆是大正方形的内切圆,同时又是小正方形的外接圆,小明随意向水平放置的大正方形内部区域抛一个小球,则小球停在小正方形内部阴影区域的概率为( )
A、 B、 C、 D、7. 下列各式计算正确的是( )A、 B、 C、 D、8. 如图,圆是大正方形的内切圆,同时又是小正方形的外接圆,小明随意向水平放置的大正方形内部区域抛一个小球,则小球停在小正方形内部阴影区域的概率为( ) A、 B、 C、 D、9. 下列命题:(1)二元一次方程的解只有一个;(2)只有一条高在内部的三角形是钝角三角形;(3)等腰三角形两腰上的高相等;(4)等腰三角形的周长是22,一边是 , 那么另一边一定是6;(5)中, , 则是直角三角形;(6)是的解集正确的个数有( )A、1个 B、2个 C、3个 D、4个10. 某专卖店专门营销某种品牌的运动服,店主对上一周中运动服的销售情况统计如下:
A、 B、 C、 D、9. 下列命题:(1)二元一次方程的解只有一个;(2)只有一条高在内部的三角形是钝角三角形;(3)等腰三角形两腰上的高相等;(4)等腰三角形的周长是22,一边是 , 那么另一边一定是6;(5)中, , 则是直角三角形;(6)是的解集正确的个数有( )A、1个 B、2个 C、3个 D、4个10. 某专卖店专门营销某种品牌的运动服,店主对上一周中运动服的销售情况统计如下:尺码
号
号
号
号
号
平均每天销售数量(套)
3
10
4
6
3
该店主本周进货时,增加了一些 号的运动服,影响该店主决策的统计量是( )
A、平均数 B、众数 C、方差 D、中位数11. 如右图所示,一个几何体恰好能通过两个小孔,这个几何体可能是( ) A、圆锥 B、三棱锥 C、四棱柱 D、三棱柱12. 方程的根的情况是( )A、方程有两个不相等的实数根 B、方程有两个相等的实数根 C、方程没有实数根 D、方程的根的情况与k的取值有关13. 如图,在△ABC中,AB=AC=10,BC=12,AD=8,AD是BC边上的高.若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是( ).
A、圆锥 B、三棱锥 C、四棱柱 D、三棱柱12. 方程的根的情况是( )A、方程有两个不相等的实数根 B、方程有两个相等的实数根 C、方程没有实数根 D、方程的根的情况与k的取值有关13. 如图,在△ABC中,AB=AC=10,BC=12,AD=8,AD是BC边上的高.若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是( ). A、6 B、8 C、9.6 D、1214. 抛物线上部分点的横坐标 , 纵坐标的对应值如下表,从下表可知:
A、6 B、8 C、9.6 D、1214. 抛物线上部分点的横坐标 , 纵坐标的对应值如下表,从下表可知:-2
-1
0
1
2
0
4
6
6
4
下列说法:①抛物线与轴的另一个交点为 , ②函数的最大值为6,③抛物线的对称轴是直线 , ④在对称轴的左侧,随的增大而增大,正确的有( )
A、1个 B、2个 C、3个 D、4个二、填空题
-
15. 分解因式:16. 若一个九边形8个外角的和为200º,则它的第9个外角为度.17. 直角三角形的两直角边是12,16,则此三角形的外接圆的半径是 .18. 如图,是的中线, , , , 则的长为 .
 19. 如图,点P在∠AOB的平分线上,PE⊥OA于E,PF⊥OB于F,若PE=3,则PF= .
19. 如图,点P在∠AOB的平分线上,PE⊥OA于E,PF⊥OB于F,若PE=3,则PF= .
三、解答题
-
20. 如图,在凯里市某广场上空飘着一只气球 , 、是地面上相距90米的两点,它们分别在气球的正西和正东,测得仰角 , 仰角 , 求气球的高度.精确到米,
 21. 计算(1)、;(2)、 .22. 某中学对全校九年级学生进行了一次数学考试,并随机抽取了部分学生的测试成绩作为样本进行分析,绘制成了如下两幅不完整的统计图,请你根据统计图中提供的信息解答下列问题:
21. 计算(1)、;(2)、 .22. 某中学对全校九年级学生进行了一次数学考试,并随机抽取了部分学生的测试成绩作为样本进行分析,绘制成了如下两幅不完整的统计图,请你根据统计图中提供的信息解答下列问题: (1)、求样本中表示成绩类别为“中”的人数,并将条形统计图补充完整;(2)、该学校九年级共有1000人参加了这次数学考试,估算该校九年级共有多少名学生的数学成绩可以达到优秀?(3)、这次数学考试成绩最优秀的四人分别来自九年三班3人和九年二班1人,学校想从这四人当中抽取两人去参加数学竞赛,被抽中的两人都来自九年三班的概率是多少?23. 图1、图2分别是的网格,网格中每个小正方形的边长均为1,线段的端点在小正方形的顶点上,请在图1、图2中各画一个图形,分别满足以下要求:
(1)、求样本中表示成绩类别为“中”的人数,并将条形统计图补充完整;(2)、该学校九年级共有1000人参加了这次数学考试,估算该校九年级共有多少名学生的数学成绩可以达到优秀?(3)、这次数学考试成绩最优秀的四人分别来自九年三班3人和九年二班1人,学校想从这四人当中抽取两人去参加数学竞赛,被抽中的两人都来自九年三班的概率是多少?23. 图1、图2分别是的网格,网格中每个小正方形的边长均为1,线段的端点在小正方形的顶点上,请在图1、图2中各画一个图形,分别满足以下要求: (1)、在图1中画一个以线段为一边的菱形(非正方形),所画菱形各顶点必须在小正方形的顶点上.(2)、在图2中画一个以线段为一边的等腰三角形,所画等腰三角形各顶点必须在小正方形的顶点上,且所画等腰三角形的面积为 .24. 一次函数y=2x+2与反比例函数y=(k≠0)的图象都过点A(1,m),y=2x+2的图象与x轴交于B点.(1)、求点B的坐标及反比例函数的表达式;(2)、C(0,﹣2)是y轴上一点,若四边形ABCD是平行四边形,直接写出点D的坐标,并判断D点是否在此反比例函数的图象上,并说明理由.25. 将矩形纸片沿对角线翻折,使点的对应点(落在矩形所在平面内,与相交于点 , 接.
(1)、在图1中画一个以线段为一边的菱形(非正方形),所画菱形各顶点必须在小正方形的顶点上.(2)、在图2中画一个以线段为一边的等腰三角形,所画等腰三角形各顶点必须在小正方形的顶点上,且所画等腰三角形的面积为 .24. 一次函数y=2x+2与反比例函数y=(k≠0)的图象都过点A(1,m),y=2x+2的图象与x轴交于B点.(1)、求点B的坐标及反比例函数的表达式;(2)、C(0,﹣2)是y轴上一点,若四边形ABCD是平行四边形,直接写出点D的坐标,并判断D点是否在此反比例函数的图象上,并说明理由.25. 将矩形纸片沿对角线翻折,使点的对应点(落在矩形所在平面内,与相交于点 , 接.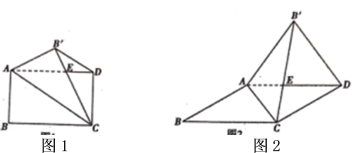 (1)、在图1中,
(1)、在图1中,①和的位置关系为;
②将剪下后展开,得到的图形是;
(2)、若图1中的矩形变为平行四边形时(),如图2所示,结论①、②是否成立,若成立,请对结论②加以证明,若不成立,请说明理由26. 如图,已知抛物线y=ax2+2x+c与y轴交于点A(0,6),与x轴交于点B(6,0),点P是线段AB上方抛物线上的一个动点. (1)、求这条抛物线的表达式及其顶点的坐标;(2)、点M在抛物线上,点N在x轴上,是否存在以点A、B、M、N为顶点的四边形是平行四边形?若存在,求出所有符合条件的点M的坐标;若不存在,请说明理由;(3)、当点P从A点出发沿线段AB上方的抛物线向终点B移动时,点P到直线AB的距离为d,求d的最大时点P的坐标.
(1)、求这条抛物线的表达式及其顶点的坐标;(2)、点M在抛物线上,点N在x轴上,是否存在以点A、B、M、N为顶点的四边形是平行四边形?若存在,求出所有符合条件的点M的坐标;若不存在,请说明理由;(3)、当点P从A点出发沿线段AB上方的抛物线向终点B移动时,点P到直线AB的距离为d,求d的最大时点P的坐标.