2021年内蒙古呼伦贝尔市额尔古纳市中考数学模拟试卷
试卷更新日期:2022-03-07 类型:中考模拟
一、单选题
-
1. 下列各数是有理数的是( )A、 B、 C、 D、0.414114111…2. 图为“”型钢材的截面,要计算其截面面积,下列给出的算式中,不正确的是( )
 A、 B、 C、 D、3. 已知某几何体的三视图如图所示,则该几何体可能是( )
A、 B、 C、 D、3. 已知某几何体的三视图如图所示,则该几何体可能是( )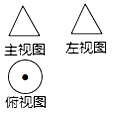 A、
A、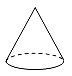 B、
B、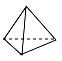 C、
C、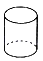 D、
D、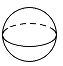 4. 若分式 有意义,则x的取值范围是( )A、x≠3 B、x≠﹣3 C、x>3 D、x>﹣35. 下列说法中,正确的是( )A、可能性很大的事情是必然发生的 B、可能性很小的事情是不可能发生的 C、如果圆的半径为 , 则该圆的周长为是必然的 D、冬季里下雪是一定发生的6. 如图,在半圆中,是直径,是的中点, , 则的度数为( )
4. 若分式 有意义,则x的取值范围是( )A、x≠3 B、x≠﹣3 C、x>3 D、x>﹣35. 下列说法中,正确的是( )A、可能性很大的事情是必然发生的 B、可能性很小的事情是不可能发生的 C、如果圆的半径为 , 则该圆的周长为是必然的 D、冬季里下雪是一定发生的6. 如图,在半圆中,是直径,是的中点, , 则的度数为( )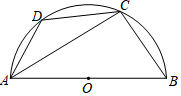 A、 B、 C、 D、7. 在2014年的体育中考中,某校6名学生的体育成绩统计如图,则这组数据的众数、中位数、方差依次是( )
A、 B、 C、 D、7. 在2014年的体育中考中,某校6名学生的体育成绩统计如图,则这组数据的众数、中位数、方差依次是( )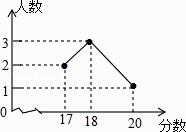 A、18,18,1 B、18,17.5,3 C、18,18,3 D、18,17.5,18. 如图,天平右盘中的每个砝码的质量都是1克,则物体A的质量m克的取值范围表示在数轴上为( )
A、18,18,1 B、18,17.5,3 C、18,18,3 D、18,17.5,18. 如图,天平右盘中的每个砝码的质量都是1克,则物体A的质量m克的取值范围表示在数轴上为( ) A、
A、 B、
B、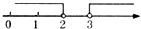 C、
C、 D、
D、 9. 如图,在 中, ,将 沿 方向平移 个单位后得到 ,连接 ,则 的长为( )
9. 如图,在 中, ,将 沿 方向平移 个单位后得到 ,连接 ,则 的长为( ) A、 B、 C、 D、10. 若正比例函数y=2kx与反比例函数(k≠0)的图象交于点A(m,1),则k的值是( )A、或 B、或 C、 D、11. 如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交B于点D,则下列说法中正确的个数是( )
A、 B、 C、 D、10. 若正比例函数y=2kx与反比例函数(k≠0)的图象交于点A(m,1),则k的值是( )A、或 B、或 C、 D、11. 如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交B于点D,则下列说法中正确的个数是( )
①AD是的平分线;②;③点D在AB的中垂线上;④:: .
A、1 B、2 C、3 D、412. 正比例函数的图象经过点 , 则( )A、2 B、 C、8 D、二、填空题
-
13. 分解因式: .14. 在我国南海某海域探明可燃冰储量约有194亿立方米,这个数据194亿立方米可以用科学记数法表示为立方米.15. 有五张正面分别标有数﹣2,0,1,3,4的纸片做成无差别的纸团,洗匀后从中任取一个纸团,若展开后将纸片上的数记为a,则使关于x的方程ax﹣1﹣3(x+1)=﹣3x的解是正整数的概率为.16. 一顶简易的圆锥形帐篷,帐篷收起来时伞面的长度有4米,撑开后帐篷高3米,则帐篷撑好后的底面直径是米.17. 如果点 , 在直线上,那么(填“>”、“<”或“=”).
三、解答题
-
18. 先化简,再求值: ,其中x=tan60°+ .19. 先化简,再求值: ÷ + ,其中a= ,b= +1.20. 数学活动课上老师带领全班学生测量旗杆高度.如图垂直于地面的旗杆顶端A垂下一根绳子.小明同学将绳子拉直钉在地上,绳子末端恰好在点C处且测得旗杆顶端A的仰角为75°;小亮同学接着拿起绳子末端向前至D处,拉直绳子,此时测得绳子末端E距离地面1.5 m且与旗杆顶端A的仰角为60°根据两位同学的测量数据,求旗杆AB的高度.(参考数据:sin75°≈0.97,cos75°≈0.26,sin60°≈0.87,结果精确到1米)
 21. 某校就“遇见路人摔倒后如何处理”的问题,随机抽取该校部分学生进行问卷调查,图1和图2是整理数据后绘制的两幅不完整的统计图.请根据图中提供的信息,解答下列问题:
21. 某校就“遇见路人摔倒后如何处理”的问题,随机抽取该校部分学生进行问卷调查,图1和图2是整理数据后绘制的两幅不完整的统计图.请根据图中提供的信息,解答下列问题: (1)、该校随机抽查了多少名学生?请将图1补充完整;(2)、在图2中,“视情况而定”部分所占的圆心角是多少度?(3)、估计该校2600名学生中采取“马上救助”的方式约有多少人?(4)、在这次调查中,甲、乙、丙、丁四名学生都选择“马上救助”,现准备从这四人中随机抽取两人进行座谈,试用列表或树形图的方法求抽取的两人恰好是甲和乙的概率.22. 如图,在等腰△ABC中,AB=BC,点D是AC边的中点,延长BD至点E,使得DE=BD,连结CE.
(1)、该校随机抽查了多少名学生?请将图1补充完整;(2)、在图2中,“视情况而定”部分所占的圆心角是多少度?(3)、估计该校2600名学生中采取“马上救助”的方式约有多少人?(4)、在这次调查中,甲、乙、丙、丁四名学生都选择“马上救助”,现准备从这四人中随机抽取两人进行座谈,试用列表或树形图的方法求抽取的两人恰好是甲和乙的概率.22. 如图,在等腰△ABC中,AB=BC,点D是AC边的中点,延长BD至点E,使得DE=BD,连结CE.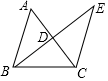 (1)、求证:△ABD≌△CED.(2)、当BC=5,CD=3时,求△BCE的周长.23. 为调动学生学习积极性,某中学初一(1)班对学生的学习表现实行每学月评分制,现对初一上期1—5学月的评分情况进行了统计,其中学生小明5次得分情况如下表所示:
(1)、求证:△ABD≌△CED.(2)、当BC=5,CD=3时,求△BCE的周长.23. 为调动学生学习积极性,某中学初一(1)班对学生的学习表现实行每学月评分制,现对初一上期1—5学月的评分情况进行了统计,其中学生小明5次得分情况如下表所示:时间
第1学月
第2学月
第3学月
第4学月
第5学月
得分
8分
9分
9分
9分
10分
学生小刚的得分情况制成了如下不完整的折线统计图:
 (1)、若小刚和小明这5次得分的平均成绩相等,求出小刚第3学月的得分,并补全折线统计图;(2)、据统计,小明和小刚这5学月的总成绩都排在了班级的前4名,现准备从该班的前四名中任选两名同学参加学校的表彰大会,请用列表或画树状图的方法,求选取的两名同学恰好是小明和小刚两人的概率.24. 如图,在中, , BD为的中线,过点作于点 , 过作BD的平行线,交的延长线与点 , 在的延长线上截取 , 连接 , 若 , , 则四边形的周长为多少?
(1)、若小刚和小明这5次得分的平均成绩相等,求出小刚第3学月的得分,并补全折线统计图;(2)、据统计,小明和小刚这5学月的总成绩都排在了班级的前4名,现准备从该班的前四名中任选两名同学参加学校的表彰大会,请用列表或画树状图的方法,求选取的两名同学恰好是小明和小刚两人的概率.24. 如图,在中, , BD为的中线,过点作于点 , 过作BD的平行线,交的延长线与点 , 在的延长线上截取 , 连接 , 若 , , 则四边形的周长为多少?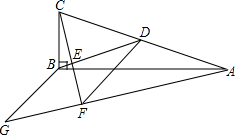 25. 为满足市场需求,某超市在新年来临前夕,购进一款商品,每盒进价是40元.超市规定每盒售价不得少于45元.根据以往销售经验发现;当售价定为每盒45元时,每天可以卖出700盒,如果每盒售价每提高1元,则每天要少卖出20盒.(1)、试求出每天的销售量y(盒)与每盒售价x(元)之间的函数关系式;(2)、要使每天销售的利润为6000元,且让顾客得到最大的实惠.售价应定为多少元?(3)、当每盒售价定为多少元时,每天销售的利润P(元)最大?最大利润是多少?26. 如图1,在平面直角坐标系中,已知点A的坐标是(3,0),并且OA=OC=3OB,动点P在过A,B,C三点的抛物线上,
25. 为满足市场需求,某超市在新年来临前夕,购进一款商品,每盒进价是40元.超市规定每盒售价不得少于45元.根据以往销售经验发现;当售价定为每盒45元时,每天可以卖出700盒,如果每盒售价每提高1元,则每天要少卖出20盒.(1)、试求出每天的销售量y(盒)与每盒售价x(元)之间的函数关系式;(2)、要使每天销售的利润为6000元,且让顾客得到最大的实惠.售价应定为多少元?(3)、当每盒售价定为多少元时,每天销售的利润P(元)最大?最大利润是多少?26. 如图1,在平面直角坐标系中,已知点A的坐标是(3,0),并且OA=OC=3OB,动点P在过A,B,C三点的抛物线上, (1)、求抛物线的解析式;(2)、是否存在点P,使得△ACP是以AC为底的等腰三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;(3)、过动点P作PE垂直于y轴于点E,交直线AC于点D,过点D作x轴的垂线,垂足为F,连接EF,以线段EF的中点G为圆心,以EF为直径作⊙G,求⊙G最小面积.
(1)、求抛物线的解析式;(2)、是否存在点P,使得△ACP是以AC为底的等腰三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;(3)、过动点P作PE垂直于y轴于点E,交直线AC于点D,过点D作x轴的垂线,垂足为F,连接EF,以线段EF的中点G为圆心,以EF为直径作⊙G,求⊙G最小面积.