2021年内蒙古呼和浩特市回民区九年级二模数学试题

试卷更新日期：2022-03-07 类型：中考模拟

进入出卷网下载

一、单选题

1. 在有理数1， $\frac{1}{2}$ ，-1，0中，最小的数是（）

A、1 B、 $\frac{1}{2}$ C、-1 D、0

查看试题解析
2. 下列计算正确的是（）

A、 $(x + y)^{2} = x^{2} + y^{2}$ B、 $2 x^{2} y + 3 x y^{2} = 5 x^{3} y^{3}$ C、 ${(- 2^{} b)}^{3} = - 8 a^{6} b^{3}$ D、 $(- x)^{5} \div x^{2} = x^{3}$

查看试题解析
3. 2019新型冠状病毒的直径是 $0 .00012mm$ ，将0.00012用科学记数法表示是（）

A、 $120 \times 10^{﹣ 6}$ B、 $12 \times 10^{- 3}$ C、 $1.2 \times 10^{﹣ 4}$ D、 $1.2 \times 10^{﹣ 5}$

查看试题解析
4. 估计 $(2 \sqrt{3} + 3 \sqrt{2}) \times \sqrt{\frac{1}{3}}$ 的值应在（）

A、4和5之间 B、5和6之间 C、6和7之间 D、7和8之间

查看试题解析
5. 若关于x的分式方程 $\frac{3 x}{x - 2}$ ＝ $\frac{m}{2 - x}$ +5的解为正数，则m的取值范围为（）

A、m＜﹣10 B、m≤﹣10 C、m≥﹣10且m≠﹣6 D、m＞﹣10且m≠﹣6

查看试题解析
6. 下列说法不正确的个数是（）
①永不相交的两条直线叫做平行线②13名同学中至少有两名同学的出生月份相同是必然事件③周长相等的所有的等腰直角三角形全等④每个内角都相等的多边形是正多边形⑤平分弦的直径垂直于弦，并且平分弦所对的弧．

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 已知二次函数y＝ax²－4ax＋6（a＞0），当自变量x分别取 $\sqrt{2}$ 、3、0时，对应的函数值分别：y₁ ， y₂ ， y₃ ，则y₁ ， y₂ ， y₃的大小关系正确的是（）

A、y₃＜y₂＜y₁ B、y₁＜y₂＜y₃ C、y₂＜y₁＜y₃ D、y₃＜y₁＜y₂

查看试题解析
8. 如图，AB是⊙O的直径，CD是弦，AE⊥CD于点E，BF⊥CD于点F．若FB＝FE＝2，FC＝1，则AC的长是（）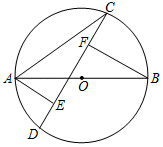

A、 $\frac{5 \sqrt{2}}{2}$ B、 $\frac{3 \sqrt{5}}{2}$ C、 $\frac{4 \sqrt{5}}{3}$ D、 $\frac{5 \sqrt{2}}{3}$

查看试题解析
9. 二次函数y＝ax²＋bx＋c（a＞0）的图像如图所示，根据图像可知，当k取（）时，关于x的方程|ax²＋bx＋c|＝k（k≠0）有两个不相等的实根

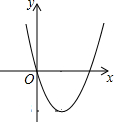A、k＞－3 B、k＞3 C、0＜k＜3 D、k＜－3

查看试题解析
10. 如图，等腰Rt△ABC中，斜边AB的长为2，O为AB的中点，P为AC边上的动点，OQ⊥OP交BC于点Q，M为PQ的中点，当点P从点A运动到点C时，点M所经过的路线长为（）

A、 $\frac{\sqrt{2}}{4} π$ B、 $\frac{\sqrt{2}}{2} π$ C、1 D、2

查看试题解析

二、填空题

11. 方程x²＝x的解为．

查看试题解析
12. 若a+b=2，ab=﹣3，则代数式a³b+2a²b²+ab³的值为．

查看试题解析
13. 若不等式组 ${\begin{array}{l} x + 4 > 2 x + 1 \\ - x > - m \end{array}$ 的解集是 $x < 3$ ，则m的取值范围是.

查看试题解析
14. 圆锥的母线长为5，侧面展开图的面积为20π，则圆锥主视图的面积为．

查看试题解析
15. 如图，直线MN∥PQ，直线AB分别与MN，PQ相交于点A，B．小宇同学利用尺规按以下步骤作图：①以点A为圆心，以任意长为半径作弧交AN于点C，交AB于点D；②分别以C，D为圆心，以大于 $\frac{1}{2}$ CD长为半径作弧，两弧在∠NAB内交于点E；③作射线AE交PQ于点F．若AB=2，∠ABP=60°，则线段AF的长为．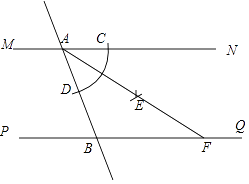

查看试题解析
16. 如图所示，在正方形ABCD的对角线上取点E，使得∠BAE=15°，连结AE，CE．延长CE到F，连结BF，使得BC=BF．若AB=1，则下列结论：①AE=CE；②F到BC的距离为 $\frac{\sqrt{2}}{2}$ ；③BE+EC=EF；④S_△_AED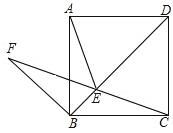= $\frac{1}{4} + \frac{\sqrt{2}}{8}$ ；⑤S_△_EBF= $\frac{\sqrt{3}}{12}$ ．其中正确的是．

查看试题解析

三、解答题

17.

(1)、计算：| $\sqrt{5}$ ﹣3|+2 $\sqrt{5}$ cos60°﹣ $\frac{1}{\sqrt{2}}$ × $\sqrt{8}$ ﹣（﹣ $\frac{\sqrt{2}}{2}$ ）⁰ ．

(2)、先化简，再求值：（x+2+ $\frac{3}{x - 2}$ ）÷ $\frac{1 + 2 x + x^{2}}{x - 2}$ ，其中x＝ $\sqrt{2}$ ﹣1．

查看试题解析
18. 已知关于x的一元二次方程x²－5x＋6＝p（p＋1）

(1)、试证明：无论p取何值，此方程总有两个实数根

(2)、若原方程的两根x₁ ， x₂满足x₁²＋x₂²－x₁x₂＝3p²＋1，求p值．

查看试题解析
19. 如图，在直角坐标系中，直线y₁＝ax＋b与双曲线y₂＝ $\frac{k}{x}$ （k≠0）分别相交于第二、四象限内的A（m，4），B（6，n）两点，与x轴相交于C点．已知OC＝3，tan∠ACO＝ $\frac{2}{3}$ ．

(1)、求y₁ ， y₂对应的函数表达式；

(2)、求△AOB的面积；

(3)、直接写出不等式ax＋b－ $\frac{k}{x}$ ＞0的解集．

查看试题解析
20. 今年2﹣4月某市出现了200名新冠肺炎患者，市委根据党中央的决定，对患者进行了免费治疗．图1是该市轻症、重症、危重症三类患者的人数分布统计图（不完整），图2是这三类患者的人均治疗费用统计图．请回答下列问题．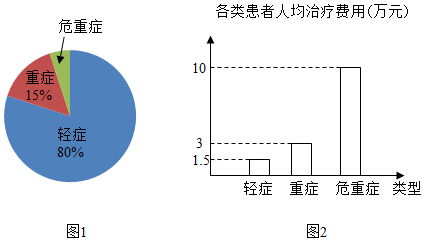

(1)、轻症患者的人数是多少？

(2)、该市为治疗危重症患者共花费多少万元？

(3)、所有患者的平均治疗费用是多少万元？

(4)、由于部分轻症患者康复出院，为减少病房拥挤，拟对某病房中的A、B、C、D、E五位患者任选两位转入另一病房，请用树状图法或列表法求出恰好选中B、D两位患者的概率．

查看试题解析
21. 为庆祝中华人民共和国七十周年华诞，某校举行书画大赛，准备购买甲、乙两种文具，奖励在活动中表现优秀的师生．已知购买 $2$ 个甲种文具、 $1$ 个乙种文具共需花费 $35$ 元；购买 $1$ 个甲种文具、 $3$ 个乙种文具共需花费 $30$ 元．

(1)、求购买一个甲种文具、一个乙种文具各需多少元？

(2)、若学校计划购买这两种文具共 $120$ 个，投入资金不少于 $955$ 元又不多于 $1000$ 元，设购买甲种文具 $x$ 个，求有多少种购买方案？

(3)、设学校投入资金 $W$ 元，在（2）的条件下，哪种购买方案需要的资金最少？最少资金是多少元？

查看试题解析
22. 如图，AB是⊙O的直径，AC是弦，P为AB延长线上一点，∠BCP＝∠BAC，∠ACB的平分线交⊙O于点D，交AB于点E，

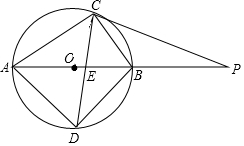(1)、求证：PC是⊙O的切线；

(2)、求证：△PEC是等腰三角形；

(3)、若AC＋BC＝2时，求CD的长．

查看试题解析
23. 设二次函数 y=ax2+bx﹣（a+b）（a，b 是常数，a≠0）．

(1)、判断该二次函数图象与 x 轴的交点的个数，说明理由．

(2)、若该二次函数图象经过 A（﹣1，4），B（0，﹣1），C（1，1）三个点中的其中两个点，求该二次函数的表达式．

(3)、若 a+b＜0，点 P（2，m）（m＞0）在该二次函数图象上，求证：a＞0．

查看试题解析
24. 回答下列题目：

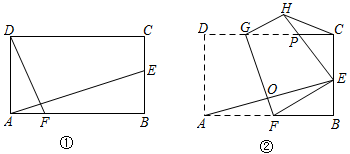(1)、如图①，在矩形ABCD中，若AB＝6，BC＝4，E，F分别是BC，AB上的点，且DF⊥AE，求 $\frac{D F}{A E}$ 的值．

(2)、如图②，在矩形ABCD中，若 $\frac{B C}{A B} = k$ （k为常数），将矩形ABCD沿GF折叠，使点A落在BC边上的点E处，得到四边形EFGH，EH交CD于点P，连接AE交GF于点O，求 $\frac{G F}{A E}$ 的值；

(3)、在（2）的条件下，连接CP，当k＝ $\frac{2}{3}$ 时，若tan∠CGH＝ $\frac{3}{4}$ ， GF＝2 $\sqrt{10}$ ，求HC的长．

查看试题解析