2021年内蒙古呼和浩特市回民区初三二模数学

试卷更新日期：2022-03-07 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列垃圾分类图标中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 某财务科为保密起见采取新的记账方式，以5万元为1个记数单位，并记100万元为0，少于100万元记为负，多于100万元记为正．例如，95万元记为－1，105万元记为1等等依此类推，75万元应该记为（）

A、－3 B、－4 C、－5 D、－6

查看试题解析
3. 下列计算中，正确的是（）

A、（a²）³•a³＝a⁹ B、（a－b）²＝a²+2ab－b² C、x²•x⁴＝x⁸ D、 $\sqrt{2} • \sqrt{3} = \sqrt{5}$

查看试题解析
4. 在一个不透明的袋子里有1个红球，2个蓝球和2个白球，这些球除颜色外都相同，从中随机摸出一个球，恰好是白球的概率是（）．

A、 $\frac{1}{5}$ B、 $\frac{1}{3}$ C、 $\frac{2}{5}$ D、 $\frac{3}{5}$

查看试题解析
5. 已知二次函数的解析式为 $y = (x - m) (x - 1)$ ， $(1 ≤ m ≤ 2)$ ，若函数过 $(a ， b)$ 和 $(a + 6 ， b)$ 两点，则 $a$ 的取值范围（）

A、 $- 2 \leq a \leq - \frac{3}{2}$ B、 $- 2 \leq a \leq - 1$ C、 $- 3 ≤ a ≤ - \frac{3}{2}$ D、 $0 \leq a \leq 2$

查看试题解析
6. 在公元前4世纪的印度巴克沙利手稿中记载着一题：甲乙丙丁四人各持金，乙为甲的二倍，丙为乙的三倍，丁为丙的四倍，并知四人持金的总数为132卢比，则乙的持金数为（）

A、4卢比 B、8卢比 C、12卢比 D、16卢比

查看试题解析
7. 关于二次函数 $y = \frac{1}{4} x^{2} - 6 x + a + 27$ ，下列说法不正确的是（）

A、若将图象向上平移10个单位，再向左平移2个单位后过点 $(4 ， 5)$ ，则 $a = - 5$ B、当 $x = 12$ 时，y有最小值 $a - 9$ C、 $x = 2$ 对应的函数值比最小值大7 D、当 $a < 0$ 时，图象与x轴有两个不同的交点

查看试题解析
8. 给出下列命题：
①对角线相等且互相平分的四边形是矩形；②对角线平分一组对角的平行四边形是菱形；③对角线互相垂直的矩形是正方形；④对角线相等的菱形是正方形；其中是真命题的有（）个．

A、1个 B、2个 C、3个 D、4个

查看试题解析
9. 如图，一次函数 $y_{1} = k x + b (k \neq 0)$ 的图象与反比例函数 $y_{2} = \frac{m}{x}$ （ $m$ 为常数且 $m \neq 0$ ）的图象都经过 $A (- 1 ， 2) ， B (2 ， - 1)$ ，结合图象，则不等式 $k x + b > \frac{m}{x}$ 的解集是（）

A、 $x < - 1$ B、 $- 1 < x < 0$ C、 $x < - 1$ 或 $0 < x < 2$ D、 $- 1 < x < 0$ 或 $x > 2$

查看试题解析
10. 如图：长方形ABCD中，AB＝3cm，AD＝9cm，将此长方形折叠，使点B与点D重合，折痕为EF，则△BEF的面积为（）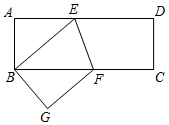

A、6cm² B、7.5cm² C、8cm² D、10cm²

查看试题解析

二、填空题

11. 分式 $\frac{1}{- a^{2} + 1} ， \frac{1}{a^{2} + a}$ 的最简公分母是， $\frac{1}{- a^{2} + 1} + \frac{1}{a^{2} + a}$ =

查看试题解析
12. 如图是一个组合几何体，右边是它的两种视图，根据图中的尺寸，这个几何体的表面积是（结果保留 $π)$ ．

查看试题解析
13. 如图，边长为2的正方形ABCD，分别以C、D为圆心，2为半径画 $\frac{1}{4}$ 圆，则阴影部分面积为．

查看试题解析
14. 为了解某校九年级学生每周的零花钱情况，随机抽取了该校100名九年级学生，他们每周的零花钱 $x$ （元）统计如下：
组别（元）
$x < 40$
$40 \leq x < 60$
$60 \leq x < 80$
$80 \leq x < 100$
人数
6
37
40
17
根据以上结果，随机抽查该校一名九年级学生，估计他每周的零花钱不低于80元的概率是．

查看试题解析
15. 一列数a₁ ， a₂ ， a₃ ， …，a_n（n为正整数），从第一个数开始．后面的每个数等于它前一个数的相反数的2倍，即a₂＝﹣2a₁ ， a₃＝﹣2a₂ ， …，a_n＝﹣2a_n_﹣1 ，若a₁＝1，则a₂₀₂₀＝．

查看试题解析
16. 以下四个命题：①用换元法解分式方程 $\frac{x^{2} + 1}{x}$ + $\frac{2 x}{x^{2} + 1}$ ＝1时，如果设 $\frac{x^{2} + 1}{x}$ ＝y，那么可以将原方程化为关于y的整式方程y²+y－2＝0；②二次函数y＝ax²－2ax+1，自变量的两个值x₁ ， x₂对应的函数值分别为y₁、y₂ ，若|x₁－1|＞|x₂－1|，则a（y₁－y₂）＞0；③有一个圆锥，与底面圆直径是 $\sqrt{3}$ 且体积为 $\frac{\sqrt{3} π}{2}$ 的圆柱等高，如果这个圆锥的侧面展开图是半圆，那么它的母线长为 $\frac{4}{3}$ ；④如果半径为r的圆的内接正五边形的边长为a，那么a＝2r sin54°．其中正确的命题的序号为

查看试题解析

三、解答题

17.

(1)、计算：2^－2－(π－2021)⁰+ $2 \sqrt{2} - \frac{1}{\sqrt{3} - 2}$ ．

(2)、解不等式组： ${\begin{array}{l} 5 x - 1 \leq 3 (x + 1) \\ \frac{3 x + 2}{2} > x \end{array}$ ，并将其解集表示在数轴上．

查看试题解析
18. 观察、思考与验证

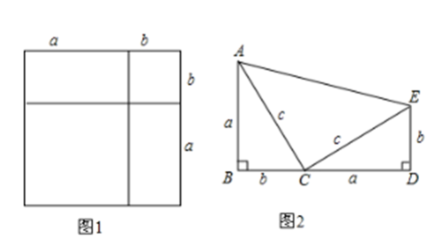(1)、如图1是一个重要公式的几何解释，请你写出这个公式．

(2)、如图2所示，∠B=∠D=90°，且B，C，D在同一直线上．试说明：∠ACE=90°．

(3)、伽菲尔德(1881年任美国第20届总统)利用(1)中的公式和图2证明了勾股定理(发表在1876年4月1日的<新英格兰教育日志》上)，请你写出验证过程．

查看试题解析
19. 如图，海面上产生了一股强台风．台风中心A在某沿海城市B的正西方向，小岛C位于城市B北偏东29°方向上，台风中心沿北偏东60°方向向小岛C移动，此时台合风中心距离小岛200海里．

(1)、过点B作 $B P ⊥ A C$ 于点P，求 $∠ P B C$ 的度数；

(2)、据监测，在距离台风中心50海里范围内均会受到台风影响（假设台风在移动过程中风力保持不变）．问：在台风移动过程中，沿海城市B是否会受到台风影响？请说明理由．（参考数： $s i n 31 ° ≈ 0.52$ ， $c o s 31 ° ≈ 0.86$ ， $t a n 31 ° \approx 0.60$ ， $\sqrt{3} \approx 1.73$ ）

查看试题解析
20. 在平面直角坐标系xOy中，反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象和 $△ A B C$ 都在第一象限内， $A B = A C = \frac{5}{2}$ ， $B C / / x$ 轴，且 $B C = 4$ ，点 $A$ 的坐标为 $(3 ， 5)$ ．

(1)、若反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象经过点B，求此反比例函数的解析式；

(2)、若将 $△ A B C$ 向下平移 $m$ （m>0）个单位长度， $A$ ， $C$ 两点的对应点同时落在反比例函数图象上，求 $m$ 的值．

查看试题解析
21. “通过等价变换，化复杂为简单，化陌生为熟悉，化未知为已知”是数学学习中解决问题的基本思维方式．例如：解方程x－ $\sqrt{x}$ ＝0，就可利用该思维方式，设 $\sqrt{x}$ ＝y，将原方程转化为：y²－y＝0这个熟悉的关于y的一元二次方程，解出y，再求x．这种方法又叫“换元法”．请你用这种思维方式和换元法解决下列问题：

(1)、填空：若2（x²+y²）²+（x²+y²）＝0，则x²+y²的值为；

(2)、解方程：x²－x+2 $\sqrt{x^{2} - x}$ －8＝0．

查看试题解析
22. 某学校开展了“我和我的祖国”主题学习竞赛活动．学校3000名学生全部参加了竞赛，结果所有学生成绩都不低于60分（满分100分）．为了了解成绩分布情况，学校随机抽取了部分学生的成绩进行统计，得到如下不完整的统计表．根据表中所给信息，解答下列问题：

(1)、表中a＝， b＝；

(2)、判断：这组数据的众数一定落在70≤x＜80范围内，这个说法（填“正确”或“错误”）；

(3)、若成绩不小于80分为优秀，则全校大约有多少名学生获得优秀成绩？
成绩x（分）分组
频数
频率
60≤x＜70
15
0.30
70≤x＜80
a
0.40
80≤x＜90
10
b
90≤x≤100
5
0.10

查看试题解析
23. 如图1，在Rt△ABC中，∠ABC＝90°，AB是⊙O的直径，⊙O交AC于点D，过点D的直线交BC于点E，交AB的延长线于点P，∠A＝∠PDB．

(1)、求证：PD是⊙O的切线；

(2)、若AB＝6，DA＝DP，试求 $\overset{⌢}{B D}$ 的长；

(3)、如图2，点M是弧AB的中点，连接DM，交AB于点N，若tanA＝ $\frac{2}{3}$ ，求 $\frac{N D}{M N}$ 的值．

查看试题解析
24. 我市某工艺厂设计了一款成本为20元/件的工艺品投放市场进行试销．经过调查，得到如表数据：
销售单价x（元/件）
…
30
40
50
60
…
每天销售量y（件）
…
500
400
300
200
…

(1)、上表中x、y的各组对应值满足一次函数关系，请求出y与x的函数关系式；

(2)、物价部门规定，该工艺品销售单价最高不能超过45元/件：
①销售单价定为多少时，工艺厂试销该工艺品每天获得的利润最大？最大利润是多少？
②该工艺厂积极投入到慈善事业，它将该工艺品每件销售利润中抽取2元捐赠给我市的公共卫生事业，并且捐款后每天的利润不低于7600元，则工艺厂每天从这件工艺品的利润中最多可捐出多少元？

查看试题解析

组别（元）	$x < 40$	$40 \leq x < 60$	$60 \leq x < 80$	$80 \leq x < 100$
人数	6	37	40	17

成绩x（分）分组	频数	频率
60≤x＜70	15	0.30
70≤x＜80	a	0.40
80≤x＜90	10	b
90≤x≤100	5	0.10

销售单价x（元/件）	…	30	40	50	60	…
每天销售量y（件）	…	500	400	300	200	…