2021年内蒙古鄂尔多斯东胜区中考二模数学试卷
试卷更新日期:2022-03-07 类型:中考模拟
一、单选题
-
1. 在数轴上表示与2的点距离2个单位长度的数是( )A、0 B、4 C、0或4 D、22. 如图是某种几何体的实物图,则与该几何体相对应的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 截止2021年4月17日,全国接种新冠病毒疫苗达到剂次,则数据表示的原数是( )A、1898000 B、18980000 C、189800000 D、18980000004. 下列运算正确的是( )A、 B、 C、 D、5. 在“博爱一日捐”活动中,某校初二级部50名教师参与献爱心,以下是捐款统计表:
3. 截止2021年4月17日,全国接种新冠病毒疫苗达到剂次,则数据表示的原数是( )A、1898000 B、18980000 C、189800000 D、18980000004. 下列运算正确的是( )A、 B、 C、 D、5. 在“博爱一日捐”活动中,某校初二级部50名教师参与献爱心,以下是捐款统计表:金额/元
50
100
150
200
300
人数
4
18
14
8
6
则该校初二教师捐款金额的中位数、众数分别是( )
A、100,100 B、100,150 C、150,100 D、150,1506. 如图,已知钝角中,且 , (1)以C为圆心,长为半径画弧;(2)以B为圆心,为半径画弧,交前弧于点E;(3)连接AE交的延长线于点D.下列叙述不一定正确的是( )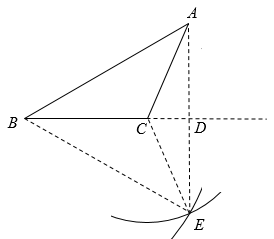 A、是等边三角形 B、平分 C、 D、BD垂直平分AE7. 随着市场对新冠疫苗需求越来越大,为满足市场需求,某大型疫苗生产企业更新技术后,加快了生产速度,现在平均每天比更新技术前多生产10万份疫苗,现在生产500万份疫苗所需的时间与更新技术前生产400万份疫苗所需时间少用5天,设现在每天生产x万份,据题意可列方程( )A、 B、 C、 D、8. 如图,四边形是半径为2的的内接四边形,连接.若 , 则的长为( )
A、是等边三角形 B、平分 C、 D、BD垂直平分AE7. 随着市场对新冠疫苗需求越来越大,为满足市场需求,某大型疫苗生产企业更新技术后,加快了生产速度,现在平均每天比更新技术前多生产10万份疫苗,现在生产500万份疫苗所需的时间与更新技术前生产400万份疫苗所需时间少用5天,设现在每天生产x万份,据题意可列方程( )A、 B、 C、 D、8. 如图,四边形是半径为2的的内接四边形,连接.若 , 则的长为( ) A、 B、 C、 D、9. 现有下列命题:①对角线相等且互相平分的四边形是矩形;②有两条边长比值是3:4的两个直角三角形相似:③若一元二次方程有实数根,则;④若点在反比例函数的图象上,且 , 则a的取值范围是 . 其中是真命题的是( )A、①② B、②③ C、③④ D、①④10. 如图1,在平行四边形中, , ;动点P以每秒1个单位的速度从点A出发沿线段运动到点B,同时动点Q以每秒4个单位的速度从点B出发,沿折线运动到点D.图2是点P、Q运动时,的面积S随运动时间t变化关系的图象,则a的值是( )
A、 B、 C、 D、9. 现有下列命题:①对角线相等且互相平分的四边形是矩形;②有两条边长比值是3:4的两个直角三角形相似:③若一元二次方程有实数根,则;④若点在反比例函数的图象上,且 , 则a的取值范围是 . 其中是真命题的是( )A、①② B、②③ C、③④ D、①④10. 如图1,在平行四边形中, , ;动点P以每秒1个单位的速度从点A出发沿线段运动到点B,同时动点Q以每秒4个单位的速度从点B出发,沿折线运动到点D.图2是点P、Q运动时,的面积S随运动时间t变化关系的图象,则a的值是( )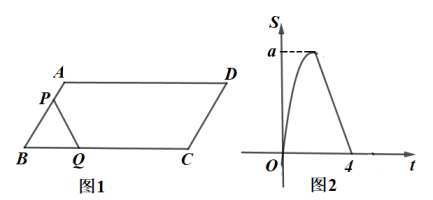 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 函数y= 中自变量x的取值范围是 .12. 如图,小明自制一块乒乓球拍,正面是半径为的 , 的长为 , 弓形(阴影部分)粘贴胶皮,则胶皮面积为 .
 13. 如图,O是坐标原点,菱形的顶点A的坐标为 , 顶点C在x轴的正半轴上,函数的图象经过顶点B,则k的值为 .
13. 如图,O是坐标原点,菱形的顶点A的坐标为 , 顶点C在x轴的正半轴上,函数的图象经过顶点B,则k的值为 . 14. 如图,点A、B、C是圆O上的三点,且四边形ABCO是平行四边形,OF⊥OC交圆O于点F,则∠BAF= .
14. 如图,点A、B、C是圆O上的三点,且四边形ABCO是平行四边形,OF⊥OC交圆O于点F,则∠BAF= . 15. 如图,在平面直角坐标系中,将绕A顺时针旋转得到 , 此时﹔将绕点顺时针旋转得到 , 此时将绕点继续顺时针旋转,此时…按此规律继续旋转,直至得到点为止,则 .
15. 如图,在平面直角坐标系中,将绕A顺时针旋转得到 , 此时﹔将绕点顺时针旋转得到 , 此时将绕点继续顺时针旋转,此时…按此规律继续旋转,直至得到点为止,则 . 16. 如图,在平面直角坐标系中,O为坐标原点, , 点B在y轴上运动,以为边作等腰 , (点A,B,C按照顺时针排列),当点B在y轴上运动时,点C也随之运动.在点C的运动过程中,的最小值为 .
16. 如图,在平面直角坐标系中,O为坐标原点, , 点B在y轴上运动,以为边作等腰 , (点A,B,C按照顺时针排列),当点B在y轴上运动时,点C也随之运动.在点C的运动过程中,的最小值为 .
三、解答题
-
17.(1)、解不等式组 , 并求出其整数解.(2)、先化简,再求值: , 其中 .18. 某中学开展了“师生共读”,营造"书香校园"的读书活动.为了了解学生在此次活动中的读书情况,现随机抽取部分学生进行调查,将收集到的数据整理,并绘制成如图所示不完整的折线统计图和扇形统计图.
 (1)、本次调查共随机抽取名学生,阅读量为2本学生所在扇形的圆心角度数是度,并补全折线统计图;(2)、根据调查情况,现决定在读书数量为1本和4本的学生中任选两名学生进行交流,请用树状图或列表法求这两名学生读书数量均为1本的概率.19. A、B两地相距400千米,某人开车从A地匀速到B地,设小汽车的行驶时间为t小时,行驶速度为v千米/小时,且全程限速,速度不超过100千米/小时.(1)、写出v关于t的函数表达式;(2)、若某人开车的速度不超过每小时80千米,那么他从A地匀速行驶到B地至少要多长时间?(3)、若某人上午7点开车从A地出发,他能否在10点40分之前到达B地?请说明理由.20. 阅读以下文字并解答问题:在“测量物体的高度”活动中,某数学兴趣小组的3名同学选择了测量学校里的三棵树的高度,在同一时刻的阳光下,他们分别做了以下工作:
(1)、本次调查共随机抽取名学生,阅读量为2本学生所在扇形的圆心角度数是度,并补全折线统计图;(2)、根据调查情况,现决定在读书数量为1本和4本的学生中任选两名学生进行交流,请用树状图或列表法求这两名学生读书数量均为1本的概率.19. A、B两地相距400千米,某人开车从A地匀速到B地,设小汽车的行驶时间为t小时,行驶速度为v千米/小时,且全程限速,速度不超过100千米/小时.(1)、写出v关于t的函数表达式;(2)、若某人开车的速度不超过每小时80千米,那么他从A地匀速行驶到B地至少要多长时间?(3)、若某人上午7点开车从A地出发,他能否在10点40分之前到达B地?请说明理由.20. 阅读以下文字并解答问题:在“测量物体的高度”活动中,某数学兴趣小组的3名同学选择了测量学校里的三棵树的高度,在同一时刻的阳光下,他们分别做了以下工作: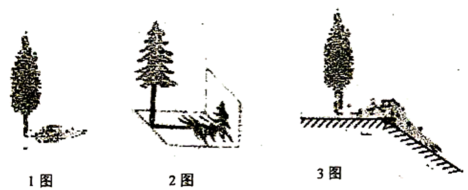
小芳:测得一根长为1米的竹竿的影长为0.8米,甲树的影长为4.08米(如1图).
小华:发现乙树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如2图),墙壁上的影长为1.2米,落在地面上的影长为2.4米.
小明:测得丙树落在地面上的影长为2.4米,落在坡面上影长为3.2米(如3图).身高是1.6米的小明站在坡面上,影子也都落坡面上,小芳测得他的影长为2米.
(1)、在横线上直接填写甲树的高度为米,乙树的高度为米﹔(2)、请求出丙树的高度.21. 如图,点D、E在以AB为直径的上,AE与交于点F, .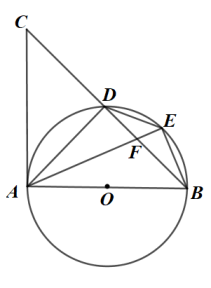 (1)、求证:是的切线;(2)、若点E是的中点, , 求的长.22. 某商店销售一种商品,经市场调查发现:该商品的周销售量y(件)是售价x(元/件)的一次函数,其售价、周销售量、周销售利润w(元)的三组对应值如表:
(1)、求证:是的切线;(2)、若点E是的中点, , 求的长.22. 某商店销售一种商品,经市场调查发现:该商品的周销售量y(件)是售价x(元/件)的一次函数,其售价、周销售量、周销售利润w(元)的三组对应值如表:售价x(元/件)
60
70
80
周销售量y(件)
100
80
60
周销售利润w(元)
2000
2400
2400
注:周销售利润=周销售量×(售价﹣进价)
(1)、①求y关于x的函数解析式.(不要求写出自变量的取值范围)②该商品进价是 ▲ 元/件;当售价是 ▲ 元/件时,周销售利润最大,最大利润是 ▲ 元.
(2)、由于某种原因,该商品进价提高了m元/件(m>0),物价部门规定该商品售价不得超过70元/件,该商店在今后的销售中,周销售量与售价仍然满足(1)中的函数关系.若周销售最大利润是1600元,求m的值.23. 如图,已知直线与抛物线相交于A,B两点,抛物线的顶点是 , 点B在x轴上. (1)、求抛物线的解析式;(2)、若点M是y轴上一点,点N是坐标平面内一点,当以A、B、M、N为顶点的四边形是矩形时,求点M的坐标.(3)、在抛物线上是否存在点Q,使 , 若存在,请直接写出点Q的横坐标;若不存在,说明理由.24.(1)、【问题发现】
(1)、求抛物线的解析式;(2)、若点M是y轴上一点,点N是坐标平面内一点,当以A、B、M、N为顶点的四边形是矩形时,求点M的坐标.(3)、在抛物线上是否存在点Q,使 , 若存在,请直接写出点Q的横坐标;若不存在,说明理由.24.(1)、【问题发现】
若四边形是菱形, , 点P是射线BD上一动点,以为边向右侧作等边 , 如图1,当点E在菱形内部或边上时,连接 , 则BP与有怎样的数量关系?并说明理由;
(2)、【类比探究】若四边形是正方形,点P是射线BD上一动点,以为直角边在边的右侧作等腰 , 其中 , 如图2.当点P在对角线BD上,点E恰好在边所在直线上时,则BP与之间的数量关系?并说明理由;
(3)、【拓展延伸】在(2)的条件下,如图3,在正方形中, , 当P是对角线BD的延长线上一动点时,连接BE,若 , 求的面积.