2021年吉林省名校调研(省命题二十二)中考数学三模试题
试卷更新日期:2022-03-07 类型:中考模拟
一、单选题
-
1. 比-3大1的数是( )A、2 B、-2 C、4 D、-42. 如图,由一个圆柱和三个正方体组成的几何体水平放置,它的左视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 不等式组 的解集在数轴上表示正确的是( )A、
3. 不等式组 的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、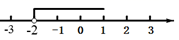 D、
D、 4. 下列运算结果是a6的是( )A、﹣(a2)3 B、a3+a3 C、(﹣2a)3 D、﹣3a8÷(﹣3a2)5. 如图摆放一副三角尺,∠B=∠EDF=90°,点E在AC上,EFBC,∠A=30°,则∠CED=( )
4. 下列运算结果是a6的是( )A、﹣(a2)3 B、a3+a3 C、(﹣2a)3 D、﹣3a8÷(﹣3a2)5. 如图摆放一副三角尺,∠B=∠EDF=90°,点E在AC上,EFBC,∠A=30°,则∠CED=( ) A、15° B、20° C、25° D、30°6. 如图,AB是⊙O的直径,点C、D在⊙O上,连接AD、CD,若∠C=28°,则若∠A的大小为( )
A、15° B、20° C、25° D、30°6. 如图,AB是⊙O的直径,点C、D在⊙O上,连接AD、CD,若∠C=28°,则若∠A的大小为( ) A、30° B、28° C、24° D、34°
A、30° B、28° C、24° D、34°二、填空题
-
7. 分解因式 .8. 每到初夏时节校园里木棉絮如雪花般漫天飞舞,经测算,木棉飞絮的直径为0.000025m左右,用科学记数法表示为 .9. 买一个篮球m元,买一个排球n元,则买6个篮球和4个排球共要元.10. 关于x的一元二次方程x2+2x+m=0有一根为2,则m的值为 .11. 如图,已知 , , ,那么 的长为 .
 12. 如图,在△ABC中,BA=BC,∠B=80°,点D在射线BC上,观察图中尺规作图的痕迹,可知∠DCE= .
12. 如图,在△ABC中,BA=BC,∠B=80°,点D在射线BC上,观察图中尺规作图的痕迹,可知∠DCE= . 13. 如图,小明将矩形纸片ABCD绕点A逆时针旋转得到矩形AEGH,点E恰好落在AC上,EG交AD于点F.若AB=3,tan∠ACB= , 则FG的长为 .
13. 如图,小明将矩形纸片ABCD绕点A逆时针旋转得到矩形AEGH,点E恰好落在AC上,EG交AD于点F.若AB=3,tan∠ACB= , 则FG的长为 . 14. 如图,在等边△ABC中.O为BC的中点,半圆O分别与AB、AC相切于点D、E.若BD=1,则图中阴影部分的面积为(结果保留根号和π).
14. 如图,在等边△ABC中.O为BC的中点,半圆O分别与AB、AC相切于点D、E.若BD=1,则图中阴影部分的面积为(结果保留根号和π).
三、解答题
-
15. 先化简,再求值: , 其中m=16. 列方程解应用题:在庆祝深圳经济特区建立40周年的活动中,八年级组购买了“小红旗”装饰各班教室,家委会先后两次在同一家商店以相同的单价购买了两种材质的“小红旗”, 第一次购买300个塑料材质的“小红旗”, 200个涤纶材质的“小红旗”,共花费660元;第二次购买100个塑料材质的“小红旗”,300个涤纶材质的“小红旗"共花费570元,求这两种材质的“小红旗”单价各为多少元?17. 如图,在四边形ABCD中,∠BAC=∠ACD=90°,CD,点E是CD的中点.求证:四边形ABCE是平行四边形.
 18. 王老师参加监考相关工作,根据学校的安排,他将被随机分到A组(考务)、B组(司时)、C组(环境消杀)、D组(安保)中的一组.(1)、王老师被分到C组(环境消杀)的概率是 .(2)、李老师也参加了此次监考工作,已知每组至少安排两位老师,请用画树状图或列表的方法,求他和王老师被分到同一组的概率.19. 如图,在平面直角坐标系中,矩形ABCO的顶点A、C分别在x轴和y轴的正半轴上,顶点B的坐标为(4,2),双曲线(x>0)的图象交BC于点D,若BD= . 求反比例函数的解析式及点F的坐标.
18. 王老师参加监考相关工作,根据学校的安排,他将被随机分到A组(考务)、B组(司时)、C组(环境消杀)、D组(安保)中的一组.(1)、王老师被分到C组(环境消杀)的概率是 .(2)、李老师也参加了此次监考工作,已知每组至少安排两位老师,请用画树状图或列表的方法,求他和王老师被分到同一组的概率.19. 如图,在平面直角坐标系中,矩形ABCO的顶点A、C分别在x轴和y轴的正半轴上,顶点B的坐标为(4,2),双曲线(x>0)的图象交BC于点D,若BD= . 求反比例函数的解析式及点F的坐标. 20. 如图,地面上小山的两侧有A,B两地,让一热气球从小山西侧A地出发沿与AB成30°角的方向,以每分钟50m的速度直线飞行,8分钟后到达点C,此时测得CB与AB成70°角,请你用测得的数据求出A、B两地的距离AB的长(结果保留整数,参考数据:≈1.7,sin20°≈0.3,cos20°≈0.9,tan20°≈0.4,sin70°≈0.9,cos70°≈0.3,tan70°≈2.7).
20. 如图,地面上小山的两侧有A,B两地,让一热气球从小山西侧A地出发沿与AB成30°角的方向,以每分钟50m的速度直线飞行,8分钟后到达点C,此时测得CB与AB成70°角,请你用测得的数据求出A、B两地的距离AB的长(结果保留整数,参考数据:≈1.7,sin20°≈0.3,cos20°≈0.9,tan20°≈0.4,sin70°≈0.9,cos70°≈0.3,tan70°≈2.7). 21. 图①、图②都是由边长为1的小等边三角形构成的网格,△ABC为格点三角形.请仅用无刻度的直尺在网格中完成下列作图,不写作法
21. 图①、图②都是由边长为1的小等边三角形构成的网格,△ABC为格点三角形.请仅用无刻度的直尺在网格中完成下列作图,不写作法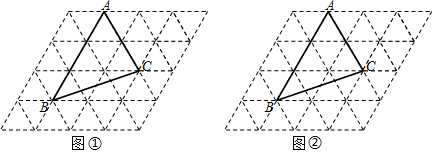 (1)、在图①中,画出△ABC中AB边上的中线CM;(2)、在图②中,画出△ABC中AC边上的高BN,并直接写出△ABC的面积.22. 为了让师生更规范地操作教室里的一体机设备,学校信息技术处制作了“教室一体机设备培训”视频,并在读报课时间进行播放.结束后为了解初中校部、高中校部各班一体机管理员对设备操作知识的掌握程度,得分用x(x为整数)表示,A:60≤x<70,B:70≤x<80,C:80≤x<90,D:90≤x≤100,对得分进行整理分析,给出了下面部分信息:
(1)、在图①中,画出△ABC中AB边上的中线CM;(2)、在图②中,画出△ABC中AC边上的高BN,并直接写出△ABC的面积.22. 为了让师生更规范地操作教室里的一体机设备,学校信息技术处制作了“教室一体机设备培训”视频,并在读报课时间进行播放.结束后为了解初中校部、高中校部各班一体机管理员对设备操作知识的掌握程度,得分用x(x为整数)表示,A:60≤x<70,B:70≤x<80,C:80≤x<90,D:90≤x≤100,对得分进行整理分析,给出了下面部分信息:初中一体机管理员的测试成绩在C组中的数据为:81,85,88.
高中一体机管理员的测试成绩:76,83,71,100,81,100,82,88,95,90,100,86,89, 93,86.
成绩统计表如下:
学部
平均数
中位数
众数
初中
88
a
98
高中
88
88
b
 (1)、a= , b= .(2)、通过以上数据分析.你认为 ▲ (填“初中”或“高中”)的一体机管理员对一体机设备操作的知识掌握的更好,请写出理由;(3)、若初中校部有100名一体机管理员,高中校部有140名一体机管理员,请估计此次浏试成绩达到90分及以上的一体机管理员共有多少人?23. 一艘游轮从甲地出发,途经乙地前往丙地,路线图如图①所示,当游轮到达乙地时,一艘货轮沿着同样的线路从甲地出发前往丙地,已知游轮的速度为 ,离开甲地的时间记为t(单位:h),两艘轮船离甲地的路程s(单位: )关于t的图象如图②所示(游轮在停靠前后的行驶速度不变).货轮比游轮早 到达丙地.
(1)、a= , b= .(2)、通过以上数据分析.你认为 ▲ (填“初中”或“高中”)的一体机管理员对一体机设备操作的知识掌握的更好,请写出理由;(3)、若初中校部有100名一体机管理员,高中校部有140名一体机管理员,请估计此次浏试成绩达到90分及以上的一体机管理员共有多少人?23. 一艘游轮从甲地出发,途经乙地前往丙地,路线图如图①所示,当游轮到达乙地时,一艘货轮沿着同样的线路从甲地出发前往丙地,已知游轮的速度为 ,离开甲地的时间记为t(单位:h),两艘轮船离甲地的路程s(单位: )关于t的图象如图②所示(游轮在停靠前后的行驶速度不变).货轮比游轮早 到达丙地.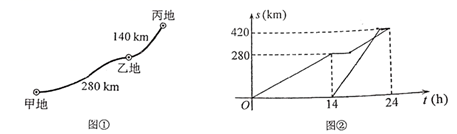
根据相关信息,解答下列问题:
(1)、填表:游轮离开甲地的时间/h
5
14
16
21
24
游轮离甲地的路程/
100
280
(2)、填空:①游轮在乙地停靠的时长为h;
②货轮从甲地到丙地所用的时长为h,行驶的速度为 ;
③游轮从乙地出发时,两艘轮船相距的路程为 .
(3)、当 时,请直接写出游轮离甲地的路程s关于t的函数解析式.24. 如图,△ABC是等腰直角三角形,∠ACB=90°,AC=BC=6,D在线段BC上,E是线段AD的一点.现以CE为直角边,C为直角顶点,在CE的下方作等腰直角△ECF,连接BF. (1)、如图1,求证:△AEC≌△BFC.(2)、当A、E、F三点共线时,如图2,若AF=2 , 求BF的长;(3)、如图3,若∠BAD=15°,连接DF,当E运动到使得∠ACE=30°时,求△CDF的面积.25. 如图,在△ABC中,∠C=90°,∠B=30°,AC=3,动点P从点B出发以每秒个单位长度的速度运动至点C,然后又在边CA上以每秒1个单位长度的速度运动至点A停止.当点P不与△ABC的顶点重合时,过点P作其所在直角边的垂线交边AB于点Q.再以PQ为边作等边△PQM,且点M与△ABC的另一条直角边始终在PQ同侧.设△PQM与△ABC重叠部分的面积为S平方单位,点P的运动时间为t秒.
(1)、如图1,求证:△AEC≌△BFC.(2)、当A、E、F三点共线时,如图2,若AF=2 , 求BF的长;(3)、如图3,若∠BAD=15°,连接DF,当E运动到使得∠ACE=30°时,求△CDF的面积.25. 如图,在△ABC中,∠C=90°,∠B=30°,AC=3,动点P从点B出发以每秒个单位长度的速度运动至点C,然后又在边CA上以每秒1个单位长度的速度运动至点A停止.当点P不与△ABC的顶点重合时,过点P作其所在直角边的垂线交边AB于点Q.再以PQ为边作等边△PQM,且点M与△ABC的另一条直角边始终在PQ同侧.设△PQM与△ABC重叠部分的面积为S平方单位,点P的运动时间为t秒.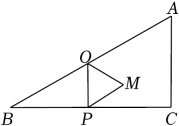 (1)、当点P在边BC上运动时.求PQ的长(用含t的代数式表示);(2)、当点P在边BC上运动时.求S与t的函数关系式;(3)、取AB的中点K,连接CK.当点M落在线段CK上时,求t的值.26. 如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)和点B(2,0).点P是x轴上方抛物线上一动点(不落在y轴上),设点P的横坐标为m,矩形PDOC的周长为L.
(1)、当点P在边BC上运动时.求PQ的长(用含t的代数式表示);(2)、当点P在边BC上运动时.求S与t的函数关系式;(3)、取AB的中点K,连接CK.当点M落在线段CK上时,求t的值.26. 如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)和点B(2,0).点P是x轴上方抛物线上一动点(不落在y轴上),设点P的横坐标为m,矩形PDOC的周长为L. (1)、求这条抛物线所对应的函数表达式.(2)、当矩形PDOC的面积被抛物线的对称轴平分时,求m的值.(3)、求L与m之间的函数关系式.(4)、设直线y=x与矩形PDOC的边交于点Q,当△OCQ为等腰直角三角形时,直接写出m的取值范围.
(1)、求这条抛物线所对应的函数表达式.(2)、当矩形PDOC的面积被抛物线的对称轴平分时,求m的值.(3)、求L与m之间的函数关系式.(4)、设直线y=x与矩形PDOC的边交于点Q,当△OCQ为等腰直角三角形时,直接写出m的取值范围.