2021年广东省珠海市斗门区中考数学一模试卷

试卷更新日期：2022-03-07 类型：中考模拟

进入出卷网下载

一、单选题

1. ﹣ $\frac{1}{2}$ 的绝对值为（）

A、﹣2 B、﹣ $\frac{1}{2}$ C、 $\frac{1}{2}$ D、1

查看试题解析
2. 2020年7月23日，中国首颗火星探测器“天问一号”顺利升空，当“天问一号”探测器抵达火星附近时，总飞行里程将达到470000000公里.470000000这个数字用科学记数法表示为（）

A、 $4.7 \times 10^{7}$ B、 $4.7 \times 10^{8}$ C、 $4.7 \times 10^{9}$ D、 $47 \times 10^{7}$

查看试题解析
3. 如图，A、B、C、D是数轴上的四个点，这四个点中最适合表示 $\sqrt{10}$ 的点是（）

A、点A B、点B C、点C D、点D

查看试题解析
4. 如图图形中，是中心对称图形但不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
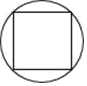5. 若方程 $x^{2} + k x - 3 = 0$ 的一个根是-3，则k的值是（）

A、-1 B、1 C、2 D、-2

查看试题解析
6. 如图，把等腰直角三角尺的直角顶点放在直尺的一边上，则∠1＋∠2的度数为（）

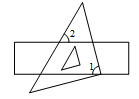A、60° B、90° C、120° D、135°

查看试题解析
7. 对于二次函数 $y = (x - 1)^{2} - 2$ 的图象，下列说法正确的是（）

A、开口向下 B、对称轴是直线 $x = - 1$ C、与 $x$ 轴有两个交点 D、顶点坐标是 $(- 1 ， - 2)$

查看试题解析
8. 直角坐标系中，点 $(- 3 ， - 1)$ 与点 $(3 ， - 1)$ 关于（）

A、 $x$ 轴轴对称 B、 $y$ 轴轴对称 C、原点中心对称 D、以上都不对

查看试题解析
9. 如图， $l_{1}$ 平行 $l_{2}$ 平行 $l_{3}$ ，下列比例式中正确的是（）

A、 $\frac{A D}{D F} = \frac{C E}{B C}$ B、 $\frac{A D}{B E} = \frac{B C}{A F}$ C、 $\frac{C E}{D F} = \frac{A D}{B C}$ D、 $\frac{A F}{D F} = \frac{B E}{C E}$

查看试题解析
10. 已知二次函数 $y = a x^{2} + b x + c$ 的图象如图所示，则一次函数 $y = a x + c$ 的图象大致是（）

A、 B、 C、 D、

查看试题解析

二、填空题

11. 因式分解： $1 - x^{2} =$ .

查看试题解析
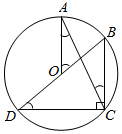
12. 不等式组 ${\begin{array}{l} x + 2 > 3 \\ \frac{x - 1}{2} < 4 \end{array}$ 的解集为．

查看试题解析
13. 一个不透明的袋子中装有2个白球和3个黑球，除颜色外其它都一样，随机摸出一个球，摸到白球的概率是．

查看试题解析
14. 如图，点 $A$ 、 $B$ 、 $C$ 在圆 $O$ 上， $B C ∥ O A$ ，连接 $B O$ 并延长，交圆 $O$ 于点 $D$ ，连接 $A C$ ， $D C$ ，若 $∠ A = 28 °$ ，则 $∠ D$ 的大小为．

查看试题解析
15. 今年春节有15名亲戚使用微信发红包给小红，结果如表：
红包数额（元 $)$
2
5
10
20
50
人数
3
4
3
4
1
则此次红包的钱数的中位数为元．

查看试题解析
16. 如图所示，矩形纸片ABCD中，AB＝4cm，BC＝8cm，现将其沿EF对折，使得点C与点A重合，则AF的长为．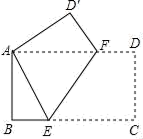

查看试题解析
17. 如图，在边长为2的正方形ABCD中，以点D为圆心.AD的长为半径画弧，再以BC为直径画半圆.若阴影部分①的面积为S₁ ，阴影部分②的面积为S₂ ，则S₂-S₁的值为.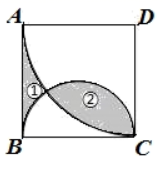

查看试题解析

三、解答题

18. 计算： $| 1 - \sqrt{2} | - 2 s i n 4 5^{°} + (\frac{1}{2})^{- 1} + (π - 2021)^{0}$ ．

查看试题解析
19. 先化简、再求值： $(2 - \frac{1}{x + 1}) \div \frac{4 x^{2} - 1}{2 x - 1}$ ，其中 $x - \sqrt{2} + 1 = 0$ ．

查看试题解析
20. 如图，在 $R t Δ A B C$ 中， $∠ C = 90 °$ ，以点 $B$ 为圆心、 $B C$ 为半径作圆弧，与边 $A B$ 交于点 $D$ ，再分别以 $A$ ． $D$ 为圆心，大于 $\frac{1}{2} A D$ 的长为半径作圆弧交于点 $M$ ， $N$ ，作直线 $M N$ ，分别交 $A C$ ， $A B$ 于点 $E$ ， $F$ ．

(1)、判断：直线 $M N$ 是线段 $A D$ 的线；

(2)、若 $B C = 5$ ， $A C = 12$ ，求 $A E$ 的长．

查看试题解析
21. 某单位在疫情期间用6000元购进 $A$ 、 $B$ 两种口罩1100个，购买 $A$ 种口罩与购买 $B$ 种口罩的费用相同，且 $A$ 种口罩的单价是 $B$ 种口罩单价的1.2倍；

(1)、求 $A$ ， $B$ 两种口罩的单价各是多少元？

(2)、随着口罩供应量不断充足， $A$ 、 $B$ 两种口罩的进价都下降了 $40 %$ ，若计划用不超过9000元的资金再次购进 $A$ 、 $B$ 两种口罩共2800个，求 $A$ 种口罩最多能购进多少个？

查看试题解析
22. 如图，在△ABC中，AB＝AC，以AB为直径的圆O分别与BC，AC交于点D，E，点F在AC边上，DF是圆O的切线．

(1)、证明：DF⊥AC；

(2)、连接OD，DE，当AC＝4FC时，判断四边形AODE的形状，并证明你的结论．

查看试题解析
23. 某市对即将参加中考的4000名初中毕业生进行了一次视力抽样调查，绘制出频数分布表和不完整的频数分布直方图．请根据图表信息回答下列问题：
初中毕业生视力抽样调查频数分布表
视力
频数（人）
频率
4.0≤x＜4.3
20
0.1
4.3≤x＜4.6
40
0.2
4.6≤x＜4.9
70
0.35
4.9≤x＜5.2
a
0.3
5.2≤x＜5.5
10
b

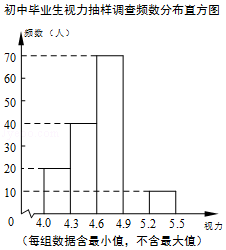(1)、本次调查样本容量为；

(2)、在频数分布表中，a＝ ▲ ， b＝ ▲ ，并将频数分布直方图补充完整；

(3)、若视力在4.9以上（含4.9）均属标准视力，根据上述信息估计全区初中毕业生中达到标准视力的学生约有多少人？

查看试题解析
24. 如图，在平面直角坐标系中， $O$ 为坐标原点，点 $B$ 在 $x$ 轴正半轴上，四边形 $O A C B$ 为平行四边形， $c o s ∠ A O B = \frac{\sqrt{3}}{3}$ ，反比例函数 $y = \frac{k}{x} (k > 0)$ 的图象在第一象限内过点 $A$ ，且经过 $B C$ 边的中点 $F$ ，连接 $A F$ ， $O F$ ．

(1)、当 $O A = \sqrt{3}$ 时，求反比例函数的表达式；

(2)、在（1）的条件下，求点 $F$ 的坐标；

(3)、证明： $Δ O A F ∽ Δ A F C$ ．

查看试题解析
25. 如图，在平面直角坐标系中，抛物线 $y = a x^{2} + b x + c$ 的对称轴为 $x = 2$ ，与 $y$ 轴交于点 $A$ 与 $x$ 轴交于点 $E$ 、 $B$ ，且点 $A (0 ， 5)$ ， $B (5 ， 0)$ ，过点 $A$ 作 $A C$ 平行于 $x$ 轴，交抛物线于点 $C$ ，点 $P$ 为抛物线上的点，且在 $A C$ 的上方，作 $P D$ 平行于 $y$ 轴交 $A B$ 于点 $D$ ．

(1)、求二次函数的解析式；

(2)、当点 $P$ 在何位置时，四边形 $A P C D$ 的面积最大？并求出最大面积；

(3)、在抛物线上是否存在点 $Q$ ，使得以点 $A$ 、 $C$ 、 $D$ 、 $Q$ 为顶点的四边形为平行四边形，如果存在，请写出点 $Q$ ， $D$ 的坐标，如果不存在，请说明理由．

查看试题解析

视力	频数（人）	频率
4.0≤x＜4.3	20	0.1
4.3≤x＜4.6	40	0.2
4.6≤x＜4.9	70	0.35
4.9≤x＜5.2	a	0.3
5.2≤x＜5.5	10	b

红包数额（元 $)$	2	5	10	20	50
人数	3	4	3	4	1