2021年广东省阳江市阳东区中考数学模拟试卷

试卷更新日期：2022-03-07 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列各实数中，属于无理数的是（）

A、 $\frac{1}{3}$ B、 $3.14$ C、0 D、 $\sqrt{5}$

查看试题解析
2. 数据2、5、6、0、6、1、8的中位数和众数分别是（）

A、0和6 B、0和8 C、5和6 D、5和8

查看试题解析
3. 已知 $a + b = \frac{1}{2}$ ，则代数式 $2 a + 2 b ﹣ 3$ 的值是（）

A、2 B、-2 C、-4 D、 $- 3 \frac{1}{2}$

查看试题解析
4. 若一个多边形的内角和为1080°，则这个多边形的边数为（）
　

A、6 B、7 C、8 D、9

查看试题解析
5. 将一张矩形纸片折叠成如图所示的图形，若∠CAB=30°，则∠ACB的度数是（）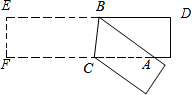

A、75° B、63° C、55° D、45°

查看试题解析
6. 将抛物线 $y = 3 x^{2}$ 向右平移4个单位长度后，再向上平移5个单位长度，所得到的抛物线的顶点坐标为（）

A、 $(4, - 5)$ B、 $(4, 5)$ C、 $(- 4, 5)$ D、 $(- 4, - 5)$

查看试题解析
7. 如图，在△AOB中，A，B两点在x轴的上方，在x轴的下方按1：2的相似比作△AOB的位似图形△A′OB′，设点B的对应点B'的坐标是（4，﹣2），则点B的坐标是（）

A、（2，1） B、（2，﹣1） C、（﹣2，1） D、（﹣2，﹣1）

查看试题解析
8. 如图，在边长为1的小正方形构成的网格中，点A，B，C都在格点上，以AB为直径的圆经过点C，D，则tan∠ADC的值为（）

A、 $\frac{2 \sqrt{13}}{13}$ B、 $\frac{3 \sqrt{13}}{13}$ C、 $\frac{2}{3}$ D、 $\frac{3}{2}$

查看试题解析
9. 关于 $x$ 的一元二次方程 $x^{2} + (1 - m) x + m^{2} = 0$ 的两个实数根互为倒数，则 $m$ 的值为（）

A、1 B、-1 C、1或-1 D、0

查看试题解析
10. 如图，四边形 $A B C D$ 为正方形， $∠ C A B$ 的平分线交 $B C$ 于点 $E$ ，将 $Δ A B E$ 绕点 $B$ 顺时针旋转 $90 °$ 得到 $Δ C B F$ ，延长 $A E$ 交 $C F$ 于点 $G$ ，连接 $B G$ ， $D G$ 与 $A C$ 相交于点 $H$ ．有下列结论：① $B E = B F$ ；② $∠ A C F = ∠ F$ ；③ $B G ⊥ D G$ ；④ $\frac{A E}{D H} = \sqrt{2}$ ，其中正确的是（）

A、①② B、②③ C、①②③ D、①②③④

查看试题解析

二、填空题

11. 因式分解： $x^{2} y - 25 y =$ ．

查看试题解析
12. 若单项式 $- \frac{1}{3} x^{2 m - 3} y^{4}$ 与3x⁵yn⁺¹的和仍是单项式，则mn＝．

查看试题解析
13. $\sqrt{x - 1} + | y + 2 | = 0$ ，则 ${(x + y)}^{2021} =$ ．

查看试题解析
14. 三角形的三边长分别为 $5$ cm， $6$ cm， $7$ cm，则连接三边中点所围成的三角形的周长是cm．

查看试题解析
15. 如图是由四个直角边长分别为2和4的全等的直角三角形拼成的“赵爽弦图”飞镖板，小明站在投镖线上向飞镖板投掷飞镖（假设投掷的飞镖均扎在飞镖板上），则针扎在阴影部分的概率是．

查看试题解析
16. 在探索数学名题“尺规三等分角”的过程中，有下面的问题：如图，AC是▱ABCD的对角线，AD＝AE＝BE，∠D＝108°，则∠BAC＝．

查看试题解析
17. 如图是由大小相同的线段组成的一系列图案，第1个图案由5条线段组成，第2个图案由8条线段组成，……，按此规律排列下去，则第2021个图案由条线段组成．

查看试题解析

三、解答题

18. 先化简，再求值： $\frac{2 y - 6}{y - 2} \div (\frac{5}{y - 2} - y - 2)$ ，其中y＝﹣1．

查看试题解析
19. 如图，在△ABD中，∠ABD＝∠ADB．

(1)、作点A关于BD的对称点C；（用尺规作图，保留作图痕迹，不要求写作法）

(2)、在（1）所作的图中，连接BC，DC．求证：四边形ABCD是菱形．

查看试题解析
20. 2021年是中国共产党成立100周年，某校组织开展了丰富多彩的主题教育活动，活动设置了A：诗歌朗诵表演，C：书画作品展览，D：手工作品展览，四个专项活动，学校随机抽取了部分学生进行调查，并根据调查结果绘制了如图所示的不完整的条形统计图和扇形统计图．

(1)、本次随机调查的学生人数是．

(2)、请你补全条形统计图；

(3)、在扇形统计图中，“B”所在扇形的圆心角为度．

(4)、若该校有学生1200人，则在这次活动中选择“A：诗歌朗诵表演”的学生有多少人？

查看试题解析
21. 如图，在边长为1的小正方形构成的网格中，点A，B是格点，连接AB，作线段AB关于直线l的对称线段A′B′，连接OA，OB，OB′，OA′．

(1)、求证：△OAB≌△OA′B′；

(2)、求以点O为圆心的劣弧AA′的长．

查看试题解析
22. 某校积极响应国家号召，为落实垃圾“分类回收，科学处理”的政策，准备购买 $100$ L和 $240$ L两种型号的垃圾箱若干套．若购买8套 $100$ L垃圾箱和5套 $240$ L垃圾箱，共需7200元；若购买4套 $100$ L垃圾箱和6套 $240$ L垃圾箱，共需6400元．

(1)、每套 $100$ L垃圾箱和每套 $240$ L垃圾箱各多少元？

(2)、学校决定购买 $100$ L垃圾箱和 $240$ L垃圾箱共20套，且 $240$ L垃圾箱的数量不少于 $100$ L垃圾箱数量的 $\frac{1}{4}$ ，求购买这20套垃圾箱的最少费用．

查看试题解析
23. 如图，在Rt△ABC中，∠BCA＝90°，AC=6，BC=8，点O在线段BC上，且OC=3，以点O为圆心，OC为半径的OO交线段AO于点D，交线段AO的延长线于点E．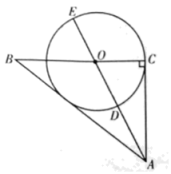

(1)、求证：AB是⊙O的切线；

(2)、求证： $\frac{D E}{A E} = \frac{A D}{D E}$ ．

查看试题解析
24. 如图，一次函数y＝kx+b（k≠0）与反比例函数 $y = \frac{m}{x} (m \neq 0 ， x > 0)$ 交于 $A$ （4， $\frac{1}{2}$ ），B（1，2），AC⊥x轴于点C，BD⊥y轴于点D．

(1)、根据图象直接回答：在第一象限内，当x取何值时，一次函数值大于反比例函数值；

(2)、求一次函数的解析式及m的值；

(3)、P是线段AB上的一点，连接PC，PD，若△BDP∽△ACP，求点P的坐标．

查看试题解析
25. 如图，点B，C分别在x轴和y轴的正半轴上，OB，OC的长分别为x²-8x+12=0的两个根（OC＞OB），点A在x轴的负半轴上，且OA=OC=3OB，连接AC．

(1)、求过A，B，C三点的抛物线的函数解析式；

(2)、点P从点C出发，以每秒2个单位长度的速度沿CA运动到点A，点Q从点O出发，以每秒1个单位长度的速度沿OC运动到点C，连接PQ，当点P到达点A时，点Q停止运动，求S_△CPQ的最大值；

(3)、M是抛物线上一点，是否存在点M，使得∠ACM=15°？若存在，请求出点M的坐标；若不存在，请说明理由．

查看试题解析