2021年广东省深圳市中考数学四模试卷

试卷更新日期：2022-03-07 类型：中考模拟

进入出卷网下载

一、单选题

1. $- \frac{2}{3}$ 的绝对值是（）

A、 $\frac{3}{2}$ B、 $- \frac{3}{2}$ C、 $\frac{2}{3}$ D、 $- \frac{2}{3}$

查看试题解析
2. 十九大报告指出，我国目前经济保持了中高速增长，在世界主要国家中名列前茅，国内生产总值从54万亿元增长80万亿元，稳居世界第二，其中80万亿用科学记数法表示为（）

A、8×10¹² B、8×10¹³ C、8×10¹⁴ D、0.8×10¹³

查看试题解析
3. 下列关于防范“新冠肺炎”的标志中既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 如图所示的几何体是由六个小正方体组合而成的，它的俯视图是（）

A、 B、 C、 D、

查看试题解析
5. 下列命题中是真命题的是（）

A、不等式 $- 3 x + 2 > 0$ 的最大整数解是 $- 1$ B、方程 $x^{2} - 3 x + 4 = 0$ 有两个不相等的实数根 C、八边形的内角和是 $1080 °$ D、三角形的内心到三角形的三个顶点的距离相等

查看试题解析
6. 某同学在今年的中考体育测试中选考跳绳．考前一周，他记录了自己五次跳绳的成绩（次数/分钟）：247，253，247，255，263．这五次成绩的平均数和中位数分别是（）

A、253，253 B、255，253 C、253，247 D、255，247

查看试题解析
7. 将一副三角板（ $∠ A ＝ 30 ° ， ∠ E ＝ 45 °$ ）按如图所示方式摆放，使得 $B A / / E F$ ，则 $∠ A O F$ 等于（）

A、 $75 °$ B、 $90 °$ C、 $105 °$ D、 $115 °$

查看试题解析
8. 如图，在△ABC中，∠B＝70°，∠C＝25°，分别以点A和点C为圆心，大于 $\frac{1}{2}$ AC的长为半径画弧，两弧相交于M，N，作直线MN，交BC于D，连接AD，则∠BAD的度数是（）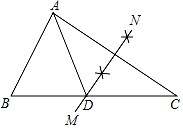

A、50° B、60° C、65° D、75°

查看试题解析
9. 二次函数y＝ax²＋bx＋c（a≠0）的顶点坐标为（﹣1，n），其部分图象如图所示，下面结论不正确的是（）

A、abc＞0 B、4ac﹣b²＜0 C、关于x的方程ax²＋bx＋c＝n＋1无实数根 D、关于x的方程ax²＋bx＋c＝0的正实数根x₁取值范围为：1＜x₁＜2

查看试题解析
10. 如图，已知四边形ABCD是边长为3的正方形，动点P从点B出发，沿BC向终点C运动，点P可以与点B、点C重合，连接PD，将 $△ P C D$ 沿直线PD折叠，设折叠后点C的对应点为点E，连接AE并延长交BC于点F，连接BE，则下列结论中：
①当 $∠ P D C = 1 5^{∘}$ 时， $△ A D E$ 为等边三角形；②当 $∠ P D C = 1 5^{∘}$ 时，F为BC的中点；③当 $P B = 2 P C$ 时， $B E ⊥ A F$ ；④当点P从点B运动到点C时，点E所走过的路径的长为 $\frac{3}{2} π .$ 其中正确的有 $($ $)$

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 因式分解： $a b^{2} - 4 a$ =.

查看试题解析
12. 在一个不透明的盒子中装有6个白球，若干个红球，它们除颜色不同外，其余均相同，若从中随机摸出一个球为白球的概率是 $\frac{2}{3}$ ，则红球的个数为.

查看试题解析
13. 定义新运算“ $a * b$ ”：对于任意实数 $a$ 、 $b$ ，都有 $a * b = (a + b) (a - b) - 1$ ，例 $4 * 3 = (4 + 3) (4 - 3) - 1 = 7 - 1 = 6$ ．若 $x * 2 = 4 x$ ，则x的值为．

查看试题解析
14. 如图，在Rt△ABC中，∠ACB=90°，AC=6，BC=8，AD平分∠CAB交BC于D点，E，F分别是AD，AC上的动点，则CE+EF的最小值为

查看试题解析
15. 如图，已知直线y=-2x+4与x轴交于点A，与y轴交于点B，将△AOB沿直线AB翻折后，设点O的对应点为点C，双曲线y= $\frac{k}{x}$ （x>0）经过点C，则k的值为．

查看试题解析

三、解答题

16. 计算：（ $\sqrt{5}$ ﹣π）⁰﹣6tan30°+（ $\frac{1}{2}$ ）^﹣²+|1﹣ $\sqrt{3}$ |

查看试题解析
17. 先化简，再求值： $(\frac{x}{x + 1} - 1) \div \frac{x^{2} - 2 x + 1}{x^{2} - 1}$ ，其中 $x = \sqrt{3} + 1$ .

查看试题解析
18. 哈佛大学一项长达20年的研究表明，爱做家务的孩子跟不爱做家务的孩子相比，就业率为15：1，收入前者比后者高20%．而且婚姻事幸福中国教育科学研究院对全国2万个学生家庭进行的调查也表明，孩子爱做家务的家庭出不爱做家务的家庭，孩子成绩优秀的比例高了27倍，为调查了解某区学生做家务的情况，随机发放调查表进行调查，要求被调查者从“A：不做家务，B：会煮饭或会做简单的菜，C：洗碗，D：保持自己的卧室清洁，E：洗衣服”五个选项中选择最常做的一项，将所有调查结果整理后绘制成如下不完整的频数分布直方图和扇形统计图．
请结合统计图回答下列问题：

(1)、本次调查中，一共调查了名市民；A、B、C、D、E五个选项的频率之和等于．

(2)、扇形统计图中，“会煮饭或会做简单的菜”对应的扇形圆心角是度

(3)、补全频数分布直方图；

(4)、若某市有小学生约24万，请你估计做家务中“洗碗”的总人数．

查看试题解析
19. 某学校为了改善办学条件，计划购置一批电子白板和台式电脑．经招投标，购买一台电子白板比购买2台台式电脑多3000元，购买2台电子白板和3台台式电脑共需2.7万元．

(1)、求购买一台电子白板和一台台式电脑各需多少元？

(2)、根据该校实际情况，购买电子白板和台式电脑的总台数为24，并且台式电脑的台数不超过电子白板台数的3倍．问怎样购买最省钱？

查看试题解析
20. 港珠澳大桥，从2009年开工建造，于2018年10月24日正式通车．其全长55公里，连接港珠澳三地，集桥、岛、隧于一体，是世界上最长的跨海大桥．如图是港珠澳大桥的海豚塔部分效果图，为了测得海豚塔斜拉索顶端A距离海平面的高度，先测出斜拉索底端C到桥塔的距离（CD的长）约为100米，又在C点测得A点的仰角为30°，测得B点的俯角为20°，求斜拉索顶端A点到海平面B点的距离（AB的长）．（已知 $\sqrt{3}$ ≈1.73，tan20°≈0.36，结果精确到0.1）

查看试题解析
21. 先阅读命题及证明思路，再解答下列问题．
命题：如图1，在正方形ABCD中，已知：∠EAF＝45°，角的两边AE、AF分别与BC、CD相交于点E、F，连接EF．求证：EF＝BE+DF．
证明思路：
如图2，将△ABE绕点A逆时针旋转90°至△ADE′．∵AB＝AD，∠BAD＝90°，∴AB与AD重合．∵∠ADC＝∠B＝90°，∴∠FDE′＝180°，点F、D、E′是一条直线．
根据SAS，得证△AEF≌△AFE′，得EF＝E′F＝E′D+DF＝BE+DF．

(1)、特例应用
如图1，命题中，如果BE＝2，DF＝3，求正方形ABCD的边长．

(2)、类比变式
如图3，在正方形ABCD中，已知∠EAF＝45°，角的两边AE、AF分别与BC、CD的延长线相交于点E、F，连接EF．写出EF、BE、DF之间的关系式，并证明你的结论．

(3)、拓展深入
如图4，在⊙O中，AB、AD是⊙O的弦，且AB＝AD，M、N是⊙O上的两点，∠MAN＝ $\frac{1}{2}$ ∠BAD．
①如图5，连接MN、MD，求证：MH＝BM+DH，DM⊥AN；
②若点C在 $\overset{⌢}{A D M}$ （点C不与点A、D、N、M重合）上，连接CB、CD分别交线段AM、AN或其延长线于点E、F，直接写出EF、BE、DF之间的等式关系．

查看试题解析
22. 平面直角坐标系中，点O是坐标原点，抛物线y＝ax²+ $\frac{3}{2}$ x+c与x轴交于A、B两点，点B的坐标为（4，0），与y轴交于点C，直线y＝kx+2经过A、C两点．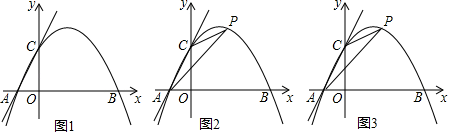

(1)、如图1，求a、c的值；

(2)、如图2，点P为抛物线y＝ax²+ $\frac{3}{2}$ x+c在第一象限的图象上一点，连接AP、CP，设点P的横坐标为t，△ACP的面积为S，求S与t的函数解析式，并直接写出自变量t的取值范围；

(3)、在（2）的条件下，点D为线段AC上一点，直线OD与直线BC交于点E，点F是直线OD上一点，连接BP、BF、PF、PD，BF＝BP，∠FBP＝90°，若OE＝ $\frac{4 \sqrt{5}}{3}$ ，求直线PD的解析式．

查看试题解析