2021年广东省深圳市坪山区九年级下学期调研测试卷 数学(一模)
试卷更新日期:2022-03-07 类型:中考模拟
一、单选题
-
1. 实数2021的相反数是( )A、2021 B、-2021 C、 D、2. 如图,由几个大小相同的小正方体组成的几何图形,则它的俯视图是( )
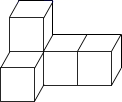 A、
A、 B、
B、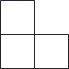 C、
C、 D、
D、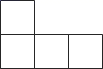 3. 深圳市卫健委2日称,截至4月2日16时,全市指定接种门诊591家,累计接种307万剂次、241万人.将241万用科学记数法表示为( )A、 B、 C、 D、4. 下列图形中既是轴对称图形又是中心对称图形的是( )A、
3. 深圳市卫健委2日称,截至4月2日16时,全市指定接种门诊591家,累计接种307万剂次、241万人.将241万用科学记数法表示为( )A、 B、 C、 D、4. 下列图形中既是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 5. 如图, , BE平分 , 若 , 则的度数为( )
5. 如图, , BE平分 , 若 , 则的度数为( ) A、34° B、32° C、22° D、56°6. 下列计算,正确的是( )A、 B、 C、 D、7. 如图,按以下步骤进行尺规作图:(1)以点为圆心,任意长为半径作弧,交的两边 , 分别于 , 两点;(2)分别以点 , 为圆心,大于的长为半径作弧,两弧在内交于点;(3)作射线 , 连接 , , . 下列结论不正确的是( )
A、34° B、32° C、22° D、56°6. 下列计算,正确的是( )A、 B、 C、 D、7. 如图,按以下步骤进行尺规作图:(1)以点为圆心,任意长为半径作弧,交的两边 , 分别于 , 两点;(2)分别以点 , 为圆心,大于的长为半径作弧,两弧在内交于点;(3)作射线 , 连接 , , . 下列结论不正确的是( ) A、垂直平分 B、 C、 D、8. 如图,在中, , C是BD上一点, , , , 则CD长为( )
A、垂直平分 B、 C、 D、8. 如图,在中, , C是BD上一点, , , , 则CD长为( ) A、 B、 C、 D、9. 如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:
A、 B、 C、 D、9. 如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:①2a+b=0;②abc>0;③方程ax2+bx+c=3有两个相等的实数根;④抛物线与x轴的另一个交点是(﹣1,0);⑤当1<x<4时,有y2<y1 ,
其中正确的是( )
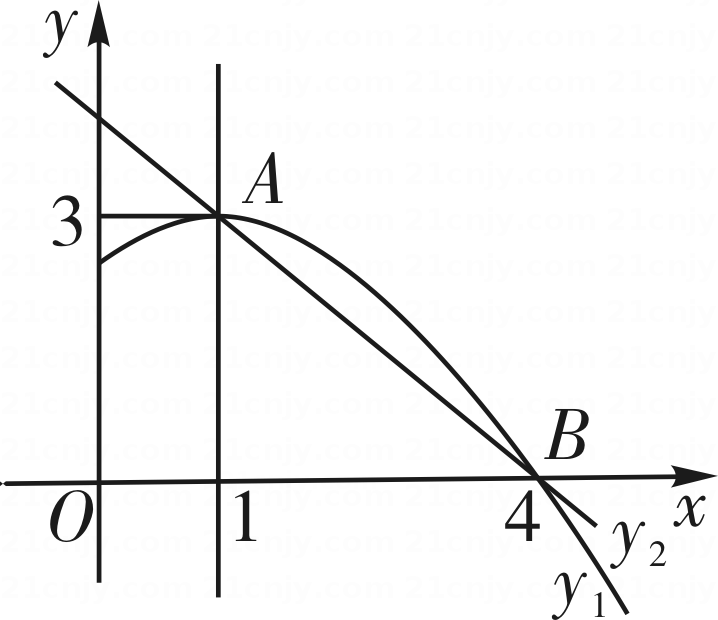 A、①②③ B、①③④ C、①③⑤ D、②④⑤10. 如图,直线分别交x、y轴于点C、D,P为反比例函数在第一象限内图象上的一点,过点P分别作x轴,y轴的垂线交直线于点A、B,且 . 下列结论:①与相似;②;③;④ . 正确的有( )
A、①②③ B、①③④ C、①③⑤ D、②④⑤10. 如图,直线分别交x、y轴于点C、D,P为反比例函数在第一象限内图象上的一点,过点P分别作x轴,y轴的垂线交直线于点A、B,且 . 下列结论:①与相似;②;③;④ . 正确的有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 分解因式: .12. 一个正方体的骰子六个面分别标有数字1、2、3、4、5、6,则扔一次骰子朝上的数字满足不等式的概率是 .13. 已知a,b为有理数,如果规定一种新的运算“※”,规定: , 例如: , 计算: .14. 在中, , , CD为AB边上中线,于点E,连接AE交BC于点F、若 , 则 .
 15. 如图,在和中, , , 点D在BC边上,AC与DE相交于点F, , 则 .
15. 如图,在和中, , , 点D在BC边上,AC与DE相交于点F, , 则 .
三、解答题
-
16. 计算 .17. 先化简,再从中选一个合适的数作为的值代入求值.18. 中华汉字,寓意深广,为了传承优秀传统文化,某校组织了一次全校3000名学生参加的“古诗词”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:

成绩/分
频数
频率
10
0.05
20
0.10
30
0.30
80
0.40
请根据所给信息,解答下列问题:
(1)、a= , b=;(2)、请补全频数分布直方图;(3)、这次比赛成绩的中位数会落在分数段;(4)、若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的3000名学生中成绩“优”等约有多少人?19. 如图,BC是的直径,A为上一点,连接AB、AC,于点D,E是直径CB延长线上一点,且AB平分 . (1)、求证:AE是的切线;(2)、若 , , 求EA.20. 为响应对口扶贫,深圳某单位和西部某乡结对帮扶,采购该乡农副产品助力乡村振兴.已知1件A产品价格比1件B产品价格少20元,300元购买A产品件数与400元购买B产品件数相同.(1)、A产品和B产品每件分别是多少元?(2)、深圳该对口单位动员职工采购该乡A、B两种农副产品,根据统计:职工响应积极,两种预计共购买150件,A的数量不少于B的2倍,求购买总费用的最大值.21. 如图1,抛物线与轴交于点、 , 与轴交于点 .
(1)、求证:AE是的切线;(2)、若 , , 求EA.20. 为响应对口扶贫,深圳某单位和西部某乡结对帮扶,采购该乡农副产品助力乡村振兴.已知1件A产品价格比1件B产品价格少20元,300元购买A产品件数与400元购买B产品件数相同.(1)、A产品和B产品每件分别是多少元?(2)、深圳该对口单位动员职工采购该乡A、B两种农副产品,根据统计:职工响应积极,两种预计共购买150件,A的数量不少于B的2倍,求购买总费用的最大值.21. 如图1,抛物线与轴交于点、 , 与轴交于点 . (1)、求抛物线的解析式;(2)、在抛物线上求点P,使 , 求点Р的坐标;(3)、如图2,直线交抛物线于第一象限的点M,若N是抛物线上一点,且 , 求点N的坐标.22. 如图1,在平面直角坐标系中,四边形AOBC为矩形,点A的坐标为 , 点B的坐标为 , 点E、F分别是BC边、AC边上的动点,均不与端点重合.连接EF,把沿着动直线EF翻折,得到 .
(1)、求抛物线的解析式;(2)、在抛物线上求点P,使 , 求点Р的坐标;(3)、如图2,直线交抛物线于第一象限的点M,若N是抛物线上一点,且 , 求点N的坐标.22. 如图1,在平面直角坐标系中,四边形AOBC为矩形,点A的坐标为 , 点B的坐标为 , 点E、F分别是BC边、AC边上的动点,均不与端点重合.连接EF,把沿着动直线EF翻折,得到 . (1)、如图1,当点C的对应点D落在AB上,且时,则;(2)、如图2,点 , 连接FG交AB于点H,直线ED交AB于点I,当四边形FHIE为平行四边形时,求CE的长;(3)、当点E、F在问题(1)中的位置时,把绕点E逆时针旋转度(得到 , 设直线与y轴、直线AB分别交于点N、M,当时,直接写出AM的长.
(1)、如图1,当点C的对应点D落在AB上,且时,则;(2)、如图2,点 , 连接FG交AB于点H,直线ED交AB于点I,当四边形FHIE为平行四边形时,求CE的长;(3)、当点E、F在问题(1)中的位置时,把绕点E逆时针旋转度(得到 , 设直线与y轴、直线AB分别交于点N、M,当时,直接写出AM的长.